探寻物理学中的 8π 项 | The Big Bang Theory “- 8πα“-优快云博客

本文链接：https://blog.youkuaiyun.com/u013669912/article/details/146365786

注：本文为 “The Big Bang Theory” 中提及的 “ $- 8 π α$ ” 及相关讨论。

机翻，未校。

In search of “eight pi” term in physics

探寻物理学中的 “ $8 π$ ” 项

Yaman Boluk
Jan 8,2023

The number of modes of vibrations per unit volume with wavelengths between $\lambda$ and $d\lambda$
单位体积内波长在 $\lambda$ 和 $\lambda + d\lambda$ 之间的振动模式数量
$n(\lambda)d\lambda = \frac{8\pi}{\lambda^{4}}d\lambda$
与黑体辐射相关的模式密度公式，描述了单位体积内不同波长的振动模式数量分布。

The rate of flux of particle across the sphere of diameter $D$
粒子穿过直径为 $D$ 的球体的通量率
$J(\infty) = 4\pi D(2a)n_{\infty} = 8\pi Dan_{\infty}$
粒子通过一定直径球体的通量率，是关于粒子流的一个物理量。

Energy per unit volume per unit wavelength
单位体积每单位波长的能量
$S_{\lambda} = \frac{8\pi hc}{\lambda^{5}}\frac{1}{e^{hc/\lambda kT}-1}$
普朗克黑体辐射公式，用于计算单位体积每单位波长的能量分布，其中涉及到普朗克常数 $h$ 、光速 $c$ 、波长 $\lambda$ 、玻尔兹曼常数 $k$ 和温度 $T$ 。

The Einstein gravitational constant
爱因斯坦引力常数
$G_{\mu\nu} \equiv R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=\frac{8\pi G}{c^{4}}T_{\mu\nu}$

One of The Big Bang Theory episodes was my favorite. It was about the national physics competition called Physics Bowl. In fact, in real life, this is organized by the American Association of Physics Teachers (APT), Sheldon was too controlling, friends kicked him out of their team. To qualify for his entry, as the rules ask that each team must consist of four people, Sheldon builds his team, which is comprised of poorly educated people. One of the members of his team is the third-floor jianitor of the Caltech Physics Department called Dimitri. According to Sheldon’s deal with him, Dimitri sits there and does not say anything during the hallenge. When the final question arrive, the score stands at 1150 for Sheldon’s team and 1175 for Leonard’s rival team. The last question is too tricky for Leonard’s team, and Leonard incorrectly guesses “8.4”.
我最喜欢《生活大爆炸》里的一集，这集讲的是一场名为 “物理杯” 的全国物理竞赛。在现实生活中，它由美国物理教师协会（APT）举办。谢尔顿控制欲太强，朋友们把他踢出了队伍。由于比赛规则要求每支队伍必须由四人组成，为了获得参赛资格，谢尔顿组建了自己的团队，成员都是文化程度不高的人。他团队中的一员是加州理工学院物理系三楼的看门人迪米特里。根据谢尔顿和他的约定，在比赛过程中迪米特里就坐在那儿，什么也不说。到了最后一题时，谢尔顿队的得分是 1150 分，莱纳德所在的对手队得分 1175 分。最后一题对莱纳德队来说太难了，莱纳德猜错成了 “8.4”。

Now it is Sheldon’s turn to answer the question. Sheldon has so far answered every question for his team but doesn’t have an answer for this one either. Suddenly, his teammate, the third-floor janitor Dimitri with his hoarse voice and accented English, utters, “minus eight pi alfa.” It was the correct answer. Dimitri reveals afterward, yes he is a janitor in California but was a physicist at Leningrad Polytechnic of former U.S.S.R. Sheldon always believes in his intellectual superiority and, shocked and denies that answer to be his official answer. This makes the rival team win.
现在轮到谢尔顿回答问题了。此前谢尔顿为他的团队答对了每一道题，但这道题他也答不上来。突然，他的队友，三楼的看门人迪米特里，用沙哑的声音、带着口音的英语说道：“- 8πα”。这是正确答案。迪米特里后来透露，他确实是加州的一名看门人，但曾是前苏联列宁格勒理工学院的物理学家。谢尔顿一直自认为才智过人，对此感到震惊，并且拒绝承认这是他团队的正式答案。这使得对手队赢得了比赛。

The final question asked to solve the following complex quantum electrodynamics equation:
决赛的题目是求解下面这个复杂的量子电动力学方程：
在这里插入图片描述

The Big Bang Theory Season 1 - Episode 13 - 15:55

This is the equation of two-particle scattering. I was told that it wouldn’t have a numerical answer, “ $- 8 π$ ” is not really the correct solution without many assumptions. Nevertheless, this episode provoked my interest, and I started hunting equations with the “ $8 π$ ” term in it.
这是一个两粒子散射方程。有人告诉我这个方程没有数值解，在没有诸多假设的情况下，“ $- 8 π$ ” 实际上并不是正确答案。尽管如此，这一集激发了我的兴趣，我开始寻找含有 “ $8 π$ ” 项的方程。

The first one I found was the derivation of the number of modes of oscillation available to electromagnetic waves in a unit volume of the cavity with wavelengths between λ and $\lambda$ :
我找到的第一个方程是关于在波长介于 λ 和 dλ 之间的单位体积腔体内，电磁波振荡模式数量的推导公式：
$\Large n (\lambda) d \lambda=\frac {8 \pi}{\lambda^{4}} d \lambda$
It was the correct part of the Rayleigh Jeans equation, albeit the prediction of the whole equation was wrong in short wavelength, which was called the ultraviolet catastrophe. Nevertheless, this term was part of Planck’s equation which predicted the black body radiation correctly without ultraviolet catastrophe and established the foundation of the theory of the quantum mechanics.
这是瑞利 - 金斯方程中正确的一部分，尽管整个方程在短波长区域的预测是错误的，这一现象被称为紫外灾难。然而，这一项也是普朗克方程的一部分，普朗克方程正确地预测了黑体辐射，避免了紫外灾难，为量子力学理论奠定了基础。
$\Large d u=\frac {8 \pi}{c^{3}} \frac {h \nu}{\left (e^{h \nu /k T}-1\right)} \nu^{2} d \nu=\frac {8 \pi h \nu^{3}}{c^{3}} \frac {1}{\left (e^{h \nu /k T}-1\right)} d \nu$

Here are some more equations with the “8π” term:
下面是更多含有 “ $8 π$ ” 项的方程：

Einstein’s gravitational constant, a constant introduced initially by Einstein that is directly related to the Newtonian constant of gravitation:
爱因斯坦引力常数，这是爱因斯坦最初引入的一个常数，与牛顿引力常数直接相关：
$\Large G_{\mu \nu} \equiv R_{\mu \nu}-\frac {1}{2} R g_{\mu \nu}=\frac {8 \pi G}{c^{4}} T_{\mu \nu}$

Small particles are bounced around randomly by Brownian motions, they may come so close to one another that Van der Waals force binds them together which is called coagulation. Smoluchowski modeled the coagulation of identical spherical particles in a stationary fluid in the absence of interactions which is nowadays called the perfect sink model.
小颗粒会因布朗运动而随机跳动，它们可能会靠得很近，以至于范德华力将它们结合在一起，这一过程称为凝聚。斯莫卢霍夫斯基对静止流体中相同球形颗粒在无相互作用情况下的凝聚进行了建模，如今这一模型被称为完美吸收体模型。
$\Large J (\infty)=4 \pi D (2 a) n_{\infty}=8 \pi D a n_{\infty}$

What is common among those equations? It is the shell volume or inverse surface area ends up either in derivation or integration in a spherical system. Can you find other equations with the “8π” term?
这些方程有什么共同之处呢？在球面系统的推导或积分过程中，最终都会出现壳层体积积或表面积的倒数。你能找到其他含有 “8π” 项的方程吗？

Shell volume $4\pi r^{2} dr$
壳层体积 $4\pi r^{2} dr$

Written by Yaman Boluk

Professor, Department of Civil and Environmental Engineering, University of Alberta

Where does this equation originate from? (found in the Big Bang Theory)

这个方程源自哪里？（出自《生活大爆炸》）

Recently, I’ve been watching “The Big Bang Theory” again and as some of you might know, it’s a series with a lot of scientific jokes in it - mostly about Physics or Mathematics. I understand most of the things mentioned in the series and whenever I don’t understand a joke, I just look up the knowledge I’m missing on Wikipedia - e.g. learnt about Schrodinger’s cat in this way.

最近，我又在看《生活大爆炸》，你们有些人可能知道，这是一部有很多科学笑话的电视剧，大多与物理或数学有关。我能理解剧中提到的大部分内容，每当我不理解某个笑话时，我就会在维基百科上查找我缺失的知识，比如我就是这样了解薛定谔的猫的。

However, at one point, I did not know how to proceed, which is why I’m asking this question. At a Physics quiz, the participants are asked to “solve” the following equation:

然而，有一次我却不知道该怎么办，这就是我提出这个问题的原因。在一次物理测验中，参与者被要求 “解” 下面这个方程：

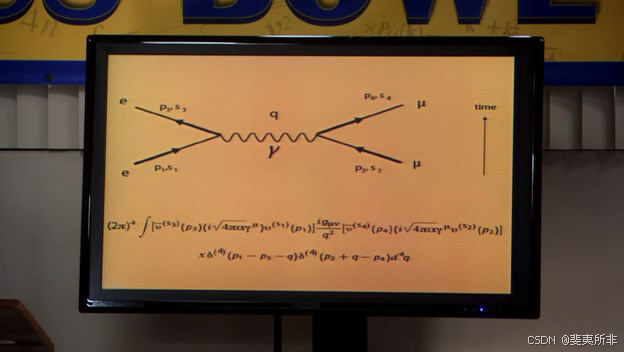
在这里插入图片描述

The solution turns out to be $\pi \alpha$ . My questions are: What is the meaning of this equation? How does one obtain it? And of course, how does one solve it and is the solution given by the university janitor (in the series) correct?

结果答案是 $\pi \alpha$ 。我的问题是：这个方程是什么意思？它是怎么来的？当然，该如何求解它，以及剧中大学门卫给出的答案正确吗？

Also, I am sorry if this is an equation found in Physics, I didn’t know.

另外，如果这是一个物理方程，我很抱歉，我并不清楚。

edited Jun 25, 2011 at 0:09

DavidZ

asked Jun 24, 2011 at 20:20

1 Answer

the feynman diagram kinda implies its physics, as does the fact that the characters are physics students (i think, never having seen the show). in other words, i don’t know - yoyo Jun 24, 2011 at 20:25

费曼图有点暗示这是物理问题，而且剧中角色是物理专业的学生（我猜的，我没看过这部剧）。换句话说，我不知道 - 悠悠 2011 年 6 月 24 日 20:25

@yoyo: Two of the characters are physics professors/researchers; another is an astrophysicist post - doc; the fourth works in the Engineering department. They all finished their degrees already. (: - Arturo Magidin Jun 24, 2011 at 20:27

@悠悠：其中两个角色是物理学教授 / 研究人员；另一个是天体物理学博士后；第四个在工程系工作。他们都已经完成了学业。（: - 阿图罗・马吉丁 2011 年 6 月 24 日 20:27

There is no equals sign in this “equation”. - Harry Stern Jun 24, 2011 at 20:31

这个 “方程” 里没有等号。 - 哈里・斯特恩 2011 年 6 月 24 日 20:31

Googling gave the following: bigbangtheory.wikia.com/wiki/The_Bat_Jar_Conjecture they mention it a bit down, I hope that helps.
– Dedalus Commented Jun 24, 2011 at 20:35

谷歌搜索结果如下：bigbangtheory.wikia.com/wiki/The_Bat_Jar_Conjecture 他们在页面下方有提及，希望这能有所帮助。 - 迪达勒斯 2011 年 6 月 24 日 20:35

The physics consultant for the show has a blog at thebigblogtheory.wordpress.com which often discusses the details of the ideas talked about in the show – though not for this particular episode.
– Mark Betnel Commented Jun 25,

该剧的物理顾问在 thebigblogtheory.wordpress.com 上有一个博客，经常讨论剧中提到的科学概念的细节，不过这一集中的内容没有涉及。 - 马克・贝内尔 2011 年 6 月 25 日 3:20

This is a so - called Feynman diagram you see on the board. It is a suggestive way to write the formula written below the diagram. Each aspect of the diagram directly translates to part of the formula via the so - called “Feynman Rules”.

你在黑板上看到的这个是所谓的费曼图。它是一种示意性的方式，用来表示图下方的公式。图的每个部分都通过所谓的“费曼规则”直接转化为公式的一部分。

With Feynman diagrams you can calculate the “amplitude” (that is related to the quantum mechanical probability for a process to happen). In this case the process is electron - muon scattering. As you can see initially there is an electron and a muon on the lower part of the diagram where the time arrow starts. The electron is on the left and carries momentum $p_{1}$ and spin $s_{1}$ . This translated to a so - called spinor $u^{(s_{1})}(p_{1})$ in the formula.

利用费曼图，你可以计算“振幅”（这与某个过程发生的量子力学概率有关）。在这个例子中，过程是电子 - 缪子散射。正如你在图中最初看到的，在时间箭头起始的下方部分有一个电子和一个缪子。电子在左边，携带动量 $p_{1}$ 和自旋 $s_{1}$ 。在公式中，这转化为一个所谓的旋量 $u^{(s_{1})}(p_{1})$ 。

The initial muon carries momentum $p_{2}$ and spin $s_{2}$ therefore its spinor is $u^{(s_{2})}(p_{2})$ .

初始缪子携带动量 $p_{2}$ 和自旋 $s_{2}$ ，因此它的旋量是 $u^{(s_{2})}(p_{2})$ 。

Now since electrons and muons are electrically charged (both are have negative charge), they will repel each other via the electromagnetic force. The “force carrier” of the EM force is the photon $\gamma$ , the quantum of the EM vector field $A_{\mu}$ . The electron and muon exchange a photon carrying momentum $q$ and represented by the term $\frac{-i g_{\mu \nu}}{q^{2}}$ .

由于电子和缪子都带电荷（都带负电），它们会通过电磁力相互排斥。电磁力的“力载体”是光子 $\gamma$ ，它是电磁矢量场 $A_{\mu}$ 的量子。电子和缪子交换一个携带动量 $q$ 的光子，在公式中用 $\frac{-i g_{\mu \nu}}{q^{2}}$ 这一项表示。

The outgoing electron with momentum $p_{3}$ and spin $s_{3}$ corresponds to the term $\bar{u}^{(s_{3})}(p_{3})$ and likewise the outgoing muon to $\bar{u}^{(s_{4})}(p_{4})$ .

出射的具有动量 $p_{3}$ 和自旋 $s_{3}$ 的电子对应于 $\bar{u}^{(s_{3})}(p_{3})$ 这一项，同样，出射的缪子对应于 $\bar{u}^{(s_{4})}(p_{4})$ 。

The strength with which the electrons and muons couple to the EM field is given by $\gamma^{\mu}$ , or as written here using the fine - structure constant $\alpha: -i \sqrt{4 \pi \alpha} \gamma^{\mu}$ .

电子和缪子与电磁场耦合的强度由 $\gamma^{\mu}$ 给出，或者在这里用精细结构常数 $\alpha$ 表示为 $\sqrt{4 \pi \alpha} \gamma^{\mu}$ 。

From these parts you construct an electron “current”

从这些部分，你可以构建一个电子“流”

$\overline{u}^{\left(s_{3}\right)}\left(p_{3}\right)\left(-i \sqrt{4 \pi \alpha} \gamma^{\mu}\right) u^{\left(s_{1}\right)}\left(p_{1}\right)$

and muon current

和缪子“流”

$\overline{u}^{\left(s_{4}\right)}\left(p_{4}\right)\left(-i \sqrt{4 \pi \alpha} \gamma^{\nu}\right) u^{\left(s_{2}\right)}\left(p_{2}\right)$

which get couple by the photon. I.e.

它们通过光子耦合。即

$\overline{u}^{\left(s_{3}\right)}\left(p_{3}\right) i \sqrt{4 \pi \alpha} \gamma^{\mu} u^{\left(s_{1}\right)}\left(p_{1}\right) \frac{-i g_{\mu \nu}}{q^{2}} \overline{u}^{\left(s_{4}\right)}\left(p_{4}\right) i \sqrt{4 \pi \alpha} \gamma^{\nu} u^{\left(s_{2}\right)}\left(p_{2}\right)$

since the exchanged momentum can be anything you have to integrate over all possible momenta $\int d^{4} q$ but make sure to conserve momentum via Dirac delta functions

由于交换的动量可以是任意值，你必须对所有可能的动量进行积分 $\int d^{4} q$ ，但要通过狄拉克 δ 函数确保动量守恒

$\delta^{(4)}\left(p_{1} - p_{3} - q\right) \delta^{(4)}\left(p_{2} + q - p_{4}\right)$

which is why you get

这就是为什么你会得到

$\begin{aligned} & \int d^{4} q \overline{u}^{\left(s_{3}\right)}\left(p_{3}\right) i \sqrt{4 \pi \alpha} \gamma^{\mu} u^{\left(s_{1}\right)}\left(p_{1}\right) \frac{-i g_{\mu \nu}}{q^{2}} \overline{u}^{\left(s_{4}\right)}\left(p_{4}\right) i \sqrt{4 \pi \alpha} \gamma^{\nu} u^{\left(s_{2}\right)}\left(p_{2}\right) \delta^{(4)}\left(p_{1} - p_{3} - q\right) \delta^{(4)}\left(p_{2} + q - p_{4}\right) \end{aligned}$