虚数 | $i^{i}$ 的多值性 / i 的几何意义

注：本文为 “虚数 $i$ ” 相关合辑。
英文引文，机翻未校。
中文引文，略作重排。
如有内容异常，请看原文。

---

$i$ to the power $i$

2023-08-08 00:00:00

The imaginary unit $i$ is defined to be the positive square root of -1. But what is $i$ to the power $i$? Is it even possible to calculate, and what does it mean?

虚数单位 $i$ 被定义为 $-1$ 的正平方根。但是 $i$ 的 $i$ 次幂是多少呢？它是否可以计算，又意味着什么呢？

As we will see, it is possible to calculate i to the power i, and the result is quite surprising in a couple of different ways. But we will start with a quick recap on the real powers of complex numbers, in particular the real powers of i.

正如我们将看到的，计算 $i$ 的 $i$ 次幂是可能的，并且结果在几个不同方面相当令人惊讶。但我们将从快速回顾复数的实幂开始，特别是 $i$ 的实幂。

Modulus-argument form for multiplication

We will be using the modulus-argument form for complex numbers, where a complex number z is represented as a radius r (called the modulus) and an angle Θ (called the argument):
我们将使用复数的模 - 辐角形式，其中复数 $z$ 表示为半径 $r$ （称为模）和角度 $\theta$ （称为辐角）：

$z=r{e}^{i\theta }$

The modulus of z is the distance from the origin to the point z on an Argand diagram. The argument of z is the angle z makes with the x-axis:
$z$ 的模是复平面上从原点到点 $z$ 的距离。 $z$ 的辐角是 $z$ 与 $x$ 轴所成的角度：

When we multiply two complex numbers z1 and z2 that are expressed in this form, the normal rules of the exponential function apply:
当我们将两个以这种形式表示的复数 $z_1$ 和 $z_2$ 相乘时，指数函数的常规规则适用：

$z_1{z}_2=r_1{e}^{i{\theta }_1}\cdot r_2{e}^{i{\theta }_2}=r_1{r}_2{e}^{i({\theta }_1+{\theta }_2)}$

We multiply the moduli r1 and r2. We add the arguments Θ1 and Θ2. That is exactly the same as we would do if the exponents were real numbers.
我们将模 $r_1$ 和 $r_2$ 相乘，将辐角 ${\theta }_1$ 和 ${\theta }_2$ 相加。这与指数为实数时的做法完全相同。

The value $i$ in modulus-argument form

We will be using i quite a lot, so it is useful to know its modulus-argument form. Here is i on an Argand diagram:
我们会经常使用 $i$ ，所以知道它的模 - 辐角形式很有用。这是复平面上的 $i$ ：

i is 1 unit vertically above the origin. So the length r is 1, and the angle is $\frac{\pi }{2}$ radians (which is 90 degrees of course). Here is the exponential form of i:
$i$ 在原点垂直上方 $1$ 个单位处。所以长度 $r$ 为 $1$ ，角度为 $\frac{\pi }{2}$ 弧度（当然也就是 $90$ 度）。这是 $i$ 的指数形式：

$i=e^{i\frac{\pi }{2}}$

If we multiply any number z by i, then in modulus-argument form this is:
如果我们将任何数 $z$ 乘以 $i$ ，那么在模 - 辐角形式下这是：

$z\cdot i=r{e}^{i\theta }\cdot e^{i\frac{\pi }{2}}=r{e}^{i(\theta +\frac{\pi }{2})}$

In other words, multiplying by z by i simply rotates z by $\frac{\pi }{2}$ radians about the origin.
换句话说，将 $z$ 乘以 $i$ 只是将 $z$ 绕原点旋转 $\frac{\pi }{2}$ 弧度。

Integer powers of i

Before calculating $i$ to the power $i$, it is worth looking at $i$ raised to a real power, as this will give us a couple of insights into the problem. We can calculate i squared like this:
在计算 $i$ 的 $i$ 次幂之前，值得看看 $i$ 的实次幂，因为这会给我们一些关于这个问题的见解。我们可以这样计算 $i$ 的平方：

$i^2=e^{i\frac{\pi }{2}}\cdot e^{i\frac{\pi }{2}}=e^{i\pi }$

This value has a unit length and an angle of $\pi$ radians (half a full turn). This makes it equal to -1. But we already know that i squared is -1, by definition. So (as expected) the modulus-argument form of i squared gives the same result as simple complex number multiplication.
这个值的长度为 $1$ ，角度为 $\pi$ 弧度（半圈）。这使得它等于 $-1$ 。但根据定义，我们已经知道 $i$ 的平方是 $-1$ 。所以（如预期的那样） $i$ 平方的模 - 辐角形式给出的结果与简单的复数乘法相同。

We can find i cubed in the same way. This time the angle is $\frac{3\pi }{2}$ radians (three-quarters of a full turn), so the result is -i:
我们可以用同样的方法找到 $i$ 的立方。这次角度是 $\frac{3\pi }{2}$ 弧度（四分之三圈），所以结果是 $-i$ ：

$i^3=e^{i\frac{\pi }{2}}\cdot e^{i\frac{\pi }{2}}\cdot e^{i\frac{\pi }{2}}=e^{i\frac{3\pi }{2}}$

i to the fourth has an angle of $2\pi$ radians a full turn), so the result is 1:
$i$ 的四次方的角度是 $2\pi$ 弧度（一圈），所以结果是 $1$ ：

$i^4=e^{i\frac{\pi }{2}}\cdot e^{i\frac{\pi }{2}}\cdot e^{i\frac{\pi }{2}}\cdot e^{i\frac{\pi }{2}}=e^{i2\pi }$

Here are i and its second, third and fourth powers plotted on an Argand diagram:
这是 $i$ 及其二次、三次和四次幂在复平面上的绘制：

It is no great surprise that i to the fourth power is 1. i to the fourth is just i squared then squared again, and since i squared is -1 then we would expect i to the fourth to be 1.
$i$ 的四次方是 $1$ 并不奇怪。 $i$ 的四次方就是 $i$ 的平方再平方，因为 $i$ 的平方是 $-1$ ，所以我们预期 $i$ 的四次方是 $1$ 。

$i^4=e^{i\frac{\pi }{2}}\cdot e^{i\frac{3\pi }{2}}\cdot e^{i\pi }\cdot e^{i\frac{\pi }{2}}=e^{i2\pi }$ 。

We can generalise this and say that i to any integer power is equal to:
我们可以推广这个结论，说 $i$ 的任何整数次幂等于：

$i^n=e^{in\frac{\pi }{2}}$

Using this we can find the fifth, sixth and seventh powers on the Argand diagram:
使用这个公式，我们可以在复平面上找到 $i$ 的第五、第六和第七次幂：

Higher integer powers of i continue rotating round and round the unit circle.
$i$ 的更高整数次幂继续绕单位圆旋转。

Takeaways

要点

There are two important takeaways from this. The first is that raising i to the power n, in modulus-argument form, works in the same way as raising any other exponential to a power n. We just multiply the exponent by n:
从这里有两个重要的要点。第一个是，将 $i$ 的 $n$ 次幂，在模 - 辐角形式下，与将任何其他指数的 $n$ 次幂的计算方式相同。我们只需将指数乘以 $n$ ：

$(e^{i\theta }{)}^n=e^{in\theta }$

The second is that there are infinitely many ways to express i in modulus argument form. Since i to the fourth is equal to 1, it follows that:
第二个是，有无限多种方式来表示 $i$ 的模 - 辐角形式。因为 $i$ 的四次方等于 $1$ ，所以：

$i=i^5=i^9=i^{13}\cdots$

In modulus-argument form:
在模 - 辐角形式下：

$e^{i\frac{\pi }{2}}=e^{i\frac{5\pi }{2}}=e^{i\frac{9\pi }{2}}=e^{i\frac{13\pi }{2}}\cdots$

In fact, for any complex number z with argument Θ, if we add an integer multiple of $2\pi$ to Θ, we will get the same number. This follows from Euler’s formula:
事实上，对于任何辐角为 $\theta$ 的复数 $z$ ，如果我们给 $\theta$ 加上 $2\pi$ 的整数倍，我们将得到相同的数。这是由欧拉公式得出的：

$e^{i\theta }=\cos \theta +i\sin \theta$

Adding a multiple of $2\pi$ to the angle does not change the value of the sine or cosine functions, because those functions are periodic with period $2\pi$ , so:
给角度加上 $2\pi$ 的倍数不会改变正弦或余弦函数的值，因为这些函数的周期是 $2\pi$ ，所以：

$\cos (\theta +2n\pi )+i\sin (\theta +2n\pi )=\cos \theta +i\sin \theta$

Integer roots of $i$

So what is the square root of i? Well, the square root of a real number x is given by raising x to the power one-half. What happens if we try the same thing with i?
那么 $i$ 的平方根是多少呢？嗯，实数 $x$ 的平方根是通过将 $x$ 提升到二分之一次幂得到的。如果我们对 $i$ 尝试同样的事情会发生什么呢？

$\sqrt{i}=(e^{i\frac{\pi }{2}}{)}^{\frac{1}{2}}=e^{i\frac{\pi }{4}}$

But remember that i can also be written as i to the power 5. If we take the square root of this alternate form we get a second square root:
但是记住 $i$ 也可以写成 $i$ 的 $5$ 次幂。如果我们对这个替代形式取平方根，我们得到第二个平方根：

$(i^5{)}^{\frac{1}{2}}=(e^{i\frac{5\pi }{2}}{)}^{\frac{1}{2}}=e^{i\frac{5\pi }{4}}$

We can draw these two roots on an Argand diagram:
我们可以在复平面上画出这两个根：

We can do this again with i to the power 9 (which is also equal to i):
我们可以对 $i$ 的 $9$ 次幂（它也等于 $i$ ）再次这样做：

$(i^9{)}^{\frac{1}{2}}=(e^{i\frac{9\pi }{2}}{)}^{\frac{1}{2}}=e^{i\frac{9\pi }{4}}=e^{i(\frac{\pi }{4}+2\pi )}$

This gives a result that has an argument of $\frac{\pi }{4}$ plus $2\pi$ . Since adding $2\pi$ has no effect on the value of a complex number, this result is identical to the original case where the argument was $\frac{\pi }{4}$ . There are only two distinct square roots of i.
这给出一个结果，其辐角为 $\frac{\pi }{4}$ 加上 $2\pi$ 。由于加上 $2\pi$ 对复数的值没有影响，这个结果与辐角为 $\frac{\pi }{4}$ 的原始情况相同。 $i$ 只有两个不同的平方根。

In fact, every complex number (except 0) has two distinct square roots, 3 distinct cube roots, and n distinct nth roots.
事实上，每个复数（除了 $0$ ）都有两个不同的平方根、三个不同的立方根和 $n$ 个不同的 $n$ 次根。

Takeaway

要点

$i$ raised to a power p can sometimes have multiple values. Those values can be found by calculating the powers of the following equivalent numbers:
$i$ 的 $p$ 次幂有时可以有多个值。这些值可以通过计算以下等价数的幂来找到：

$i^p=e^{ip\frac{\pi }{2}}$

$i^p=e^{ip(\frac{\pi }{2}+2\pi )}$

$i^p=e^{ip(\frac{\pi }{2}+4\pi )}$

$\cdots$
$i^p=e^{ip(\frac{\pi }{2}+2n\pi )}$

Not all of these roots are necessarily distinct.
并非所有这些根都一定是不同的。

$i$ to the power $i$

So now we are in a position to calculate the value of $i$ to the power i. We will assume that we can raise i to the power $i$ simply by setting p to the value i in the formula above. This can be shown to be true, but we won’t prove it here.
Here is the result:
所以现在我们可以计算 $i$ 的 $i$ 次幂的值了。我们假设可以通过在上述公式中将 $p$ 设为 $i$ 的值来计算 $i$ 的 $i$ 次幂。这可以被证明是正确的，但我们这里不进行证明。
结果如下：

$i^i=e^{i\cdot i\frac{\pi }{2}}=e^{-\frac{\pi }{2}}$

This is a very interesting result. The two $i$ terms multiply to give -1, so the exponent is now a real number. This means that the power is a real number expression!

这是一个非常有趣的结果。两个 $i$ 项相乘得到 $-1$ ，所以指数现在是一个实数。这意味着幂是一个实数表达式！
$i$ 的 $i$ 次幂就是 $-\frac{\pi }{2}$ 的指数形式。它的实数值约为 $0.207880$ 。

But it gets a little weirder. We also have to consider the other possible results based on the alternate modulus-argument forms of i. For example when n equals 1, we add 2π to the exponent:
但事情变得更奇怪了。我们还必须考虑基于 $i$ 的其他可能的模 - 辐角形式的结果。例如，当 $n=1$ 时，我们给指数加上 $2\pi$ ：

$i=e^{i(\frac{\pi }{2}+2\pi )}=e^{i\cdot \frac{5\pi }{2}}$

$i^i=e^{i\cdot i\frac{5\pi }{2}}=e^{-\frac{5\pi }{2}}$

This gives a value of approximately 0.000388203.
这给出一个约为 $0.000388203$ 的值。

We can use negative values of n too, of course. When n equals -1, we subtract 2π from the exponent:
当然，我们也可以使用 $n$ 的负值。当 $n=-1$ 时，我们从指数中减去 $2\pi$ ：

$i^i=e^{i(\frac{\pi }{2}-2\pi )}=e^{-i\frac{3\pi }{2}}$

$i^i=e^{-i\cdot i\frac{3\pi }{2}}=e^{\frac{3\pi }{2}}$

This gives a value of approximately 111.318.
这给出一个约为 $111.318$ 的值。

Since this formula is based on the exponential function of a real number, every different value of n will give a unique, real result.
由于这个公式基于实数的指数函数， $n$ 的每个不同值都会给出一个唯一的实结果。

So i to the power i has an infinite number of solutions, and they are all real numbers.
所以 $i$ 的 $i$ 次幂有无限多个解，并且它们都是实数。

---

What Is $i$ Raised To The Power $i$ ?

2023-10-19 00:00:00

虚数虚次幂的特性与多值性

An imaginary number raised to an imaginary number turns out to be real. However, while learning complex analysis, one learns that an exponential with respect to an imaginary number does not have a single, fixed value. Rather, the function is multi-valued — the value we arrived at in our calculation is just one of many values.
虚数的虚数次幂结果是实数。然而，在学习复分析时，人们会了解到关于虚数的指数函数并不具有单一、固定的值。确切地说，该函数是多值的——我们在计算中得到的值只是众多值中的一个。

虚数单位 $i$ 的定义与背景

The imaginary unit $i$ represents the square root of $-1$ , such that $i^2=-1$ . Imaginary numbers live in a world of their own; the numbers are counted on an entirely different plane or axis that is solely devised for them. However, imaginary numbers have acquired a somewhat nefarious reputation, considering that their discovery has compounded the difficulty of problems that math was already replete with. I mean, as if the numbers we already had weren’t enough?
虚数单位 $i$ 表示 $-1$ 的平方根，即 $i^2=-1$ 。虚数存在于它们自己的世界中；这些数是在一个完全不同的平面或轴上计数的，而这个平面或轴是专门为它们设计的。然而，虚数却获得了一个有点不好的名声，因为它们的发现增加了数学原本就充满的问题的难度。我的意思是，好像我们已有的数还不够多似的？

问题提出：$i^i$ 的实数特性

Our problem, however, combines not just one, but two of the many haunting aspects of mathematics. If $i$ itself is so difficult to comprehend, what could $i^i$ be? You might be surprised to know that unlike $i$ , the value of $i^i$ is a real number! How is that possible?
然而，我们的问题不仅结合了数学中众多令人困扰的方面中的一个，而是两个。如果 $i$ 本身就如此难以理解，那么 $i^i$ 会是什么呢？你可能会惊讶地知道，与 $i$ 不同， $i^i$ 的值是一个实数！这怎么可能呢？

对数运算的基本概念复习

First, we must revise one of the most common, but least understood, mathematical operations — logarithms. Let me remind you how they work: If $a=b^c$ , then ${\log }_{b}a=c$ . For instance, given that $10=10^1$ , ${\log }_{10}10=1$ . Here, $b$ is called the base of the logarithmic operation.
首先，我们必须复习一个最常见但却最不被理解的数学运算——对数。让我提醒你它们是如何工作的：如果 $a=b^c$ ，那么 ${\log }_{b}a=c$ 。例如，已知 $10=10^1$ ，则 ${\log }_{10}10=1$ 。在这里， $b$ 被称为对数运算的底数。

Log scale (Photo Credit : Saim Tokacoglu/Shutterstock) 对数刻度尺

自然对数与欧拉数 $e$

To solve the problem at hand, the base of our operation is $e$ , or Euler’s number, with a value of $2.71828\cdots$ .
为了解决手头的问题，我们运算的底数是 $e$ ，即欧拉数，其值为 $2.71828\cdots$。

If $e^y=x$ , then ${\log }_{e}x=y$ . The logarithm with the base $e$ is known as a “natural logarithm”. It is imperative to understand that the exponential and logarithmic functions are inverse functions. This is very important for our calculation.
如果 $e^y=x$ ，那么 ${\log }_{e}x=y$ 。以 $e$ 为底的对数被称为“自然对数”。必须理解指数函数和对数函数是反函数。这对我们的计算非常重要。

${\log }_e{e}^x=x\because \log a^b=b\log a$

$e^{{\log }_{e}x}=x\because {\log }_{e}x=y\text{ and }{e}^y=x$

欧拉公式与虚数单位的指数表示

The second thing to recall is that $i$ can be written as a complex number $z=0+i$ ， which can also be written as $z=\cos (\frac{\pi }{2})+i\sin (\frac{\pi }{2})$ 。 However, according to Euler’s formula, $e^{ix}=\cos (x)+i\sin (x)$ 。 Therefore, $\cos (\frac{\pi }{2})+i\sin (\frac{\pi }{2})$ is equal to $e^{i\frac{\pi }{2}}$ 。
第二件要回忆的事情是 $i$ 可以写成一个复数 $z=0+i$ ，它也可以写成 $z=\cos (\frac{\pi }{2})+i\sin (\frac{\pi }{2})$ 。然而，根据欧拉公式， $e^{ix}=\cos (x)+i\sin (x)$ 。因此， $\cos (\frac{\pi }{2})+i\sin (\frac{\pi }{2})$ 等于 $e^{i\frac{\pi }{2}}$ 。

$i=e^{i\frac{\pi }{2}}$

$i^i$ 的具体计算过程

Now, let’s say $i^i=A$ 。 Applying logarithm on both sides of the equation, we get:
现在，假设 $i^i=A$ 。在等式两边取对数，我们得到：

$i^i=A$

${\log }_e{i}^i={\log }_{e}A$

$i{\log }_{e}i={\log }_{e}A$

$i{\log }_e{e}^{i\frac{\pi }{2}}={\log }_{e}A$

Remember that logarithmic and exponential functions are inverse functions, such that ${\log }_e{e}^x=x$ 。 Thus, from the above expression, one can discern:
记住对数函数和指数函数是反函数，即 ${\log }_e{e}^x=x$ 。因此，从上面的表达式中，可以看出：

$i\cdot i\frac{\pi }{2}={\log }_{e}A$

$i^2\frac{\pi }{2}={\log }_{e}A$

$-\frac{\pi }{2}={\log }_{e}A$

Applying the exponential on both sides of the equation:
在等式两边取指数：

$e^{-\frac{\pi }{2}}=e^{{\log }_{e}A}$

Again, we encounter the inverse functions together. They neutralize to give the outcome:
再次，我们遇到了反函数在一起的情况。它们相互抵消得到结果：

$e^{-\frac{\pi }{2}}=A$

$i^i=e^{-\frac{\pi }{2}}$

$i^i\approx 0.20788$

复分析中的多值性解释

Thus, an imaginary number raised to an imaginary number turns out to be real. However, while learning complex analysis, one learns that an exponential with respect to $i$ does not have a single, fixed value. Rather, the function is multi-valued — the value we arrived at in our calculation is just one of many values. This is because the value of $i$ isn’t particularly $\cos (\frac{\pi }{2})+i\sin (\frac{\pi }{2})$ ， but $\cos (\frac{3\pi }{2})+i\sin (\frac{3\pi }{2})$ ， $\cos (\frac{5\pi }{2})+i\sin (\frac{5\pi }{2})$ and every odd multiple of $\frac{\pi }{2}$ 。 Therefore, the value of $i^i$ also varies from $e^{-\frac{\pi }{2}}$ to $e^{-\frac{3\pi }{2}}$ ， $e^{-\frac{5\pi }{2}}$ and so on.
因此，虚数的虚数次幂结果是实数。然而，在学习复分析时，人们会了解到关于 $i$ 的指数函数并不具有单一、固定的值。确切地说，该函数是多值的——我们在计算中得到的值只是众多值中的一个。这是因为 $i$ 的值不只是 $\cos (\frac{\pi }{2})+i\sin (\frac{\pi }{2})$ ，还有 $\cos (\frac{3\pi }{2})+i\sin (\frac{3\pi }{2})$ ， $\cos (\frac{5\pi }{2})+i\sin (\frac{5\pi }{2})$ 以及 $\frac{\pi }{2}$ 的每一个奇数倍。因此， $i^i$ 的值也从 $e^{-\frac{\pi }{2}}$ 变化到 $e^{-\frac{3\pi }{2}}$ ， $e^{-\frac{5\pi }{2}}$ 等等。

---

虚数的直观阐释：图解虚数 i 的意义

原文作者：阮一峰 发表日期： 2012 年 9 月 24 日

注：本文对原文有重排，删增。
原文图片 csdn 转储失败，全部重传。

一、虚数的起源与定义

1. 从矛盾到创新的数学突破

中学阶段对虚数的定义常为：$-1$ 的平方根，即
$$i=\sqrt{-1}$$
这一表述易引发困惑：何种实数的平方为负数？事实上，虚数的本质并非传统数值，而是旋转操作的代数化表达。

2. 几何视角下的虚数单位

在数轴上，+1 逆时针旋转 180° 变为 -1，

该过程等价于两次 90° 旋转，

$$(+1)\times (\text{逆时针旋转}90^{\circ }{)}^2=-1$$
将 “逆时针旋转 90°” 记作虚数单位 $i$，则有：
$$i^2=-1$$
结论：$i$ 本质是二维平面内的旋转变换算子，而非实数范畴的数。

二、复数平面与代数表示

1. 二维数系的构建

将实数轴（横轴）与虚数轴（纵轴）结合，构成复平面。任意复数 $a+bi$ 对应复平面内坐标为 $(a,b)$ 的点，其中：

• $a$ 为实部，对应横轴分量；
• $b$ 为虚部系数，对应纵轴分量。

2. 复数的双重属性

复数兼具代数形式与几何意义：

• 代数形式：$z=a+bi$（$a,b\in \mathbb{R}$）；
• 几何意义：复平面内从原点到 $(a,b)$ 的向量，可表示为旋转角度与模长的组合。

三、复数的基本运算及物理意义

1. 加法运算：矢量合成法则

代数规则：实部与虚部分别相加，如：

$$(3+i)+(1+3i)=(3+1)+(1+3)i=4+4i$$
物理意义：对应力、速度等矢量的合成，符合平行四边形法则。

2. 乘法运算：旋转与缩放的复合

几何本质：两复数相乘等价于 “模长相乘，角度相加”。

• 比如，一条船的航向是 $3+4i$

• 45°旋转对应的复数为 $1+i$，则新航向为：
  $$(3+4i)\times (1+i)=-1+7i$$
  
• 若逆时针旋转 90°（对应复数 $i$），则新航向为：
  $$(3+4i)\times i=-4+3i$$

四、复数乘法的数学证明

1. 极坐标表示法

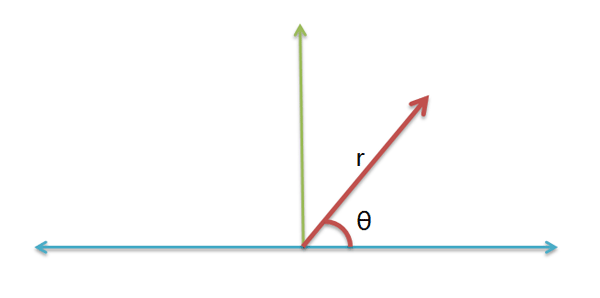
任意复数可表示为模长 $r$ 与幅角 $\theta$ 的形式：
$$a+bi=r(\cos \theta +i\sin \theta ),r=\sqrt{a^2+b^2},\theta =\arctan \frac{b}{a}$$

2. 三角恒等式推导

设两复数 $z_1=r_1(\cos \alpha +i\sin \alpha )$，$z_2=r_2(\cos \beta +i\sin \beta )$，则：
$$z_1{z}_2=r_1{r}_2[(\cos \alpha \cos \beta -\sin \alpha \sin \beta )+i(\cos \alpha \sin \beta +\sin \alpha \cos \beta )]$$
根据三角函数和角公式：
$$\begin{gathered} \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta , \\ \sin (\alpha +\beta )=\cos \alpha \sin \beta +\sin \alpha \cos \beta , \end{gathered}$$
可得：
$$z_1{z}_2=r_1{r}_2[\cos (\alpha +\beta )+i\sin (\alpha +\beta )]$$
结论：复数乘法对应旋转变换的角度叠加与模长缩放。

两复数相乘的几何意义为：模长（旋转半径）相乘，旋转角度相加，即复数乘法对应二维平面内的旋转变换与缩放变换的复合操作。

五、虚数与复数的实际应用

1. 物理学中的旋转与相位分析

• 交流电分析：用复数表示电压、电流的幅值与相位差，可以简化交流电路的分析和计算。例如，复数形式的电压和电流可以直接用于计算阻抗和功率。
• 量子力学：波函数用复数描述粒子的概率幅，这使得波函数的叠加和干涉现象可以通过复数的代数运算来处理。

2. 工程与信号处理

• 电路设计：借助复数简化阻抗计算，特别是在交流电路中，复数形式的阻抗（阻抗矩阵）可以简化电路的分析和设计。
• 傅里叶变换：复数形式用于分析周期性信号的频率成分，傅里叶变换将时间域信号转换为频率域信号，复数形式的傅里叶变换使得信号处理和分析更加直观和高效。

3. 数学工具的统一性

虚数将代数运算（加减乘除）与几何变换（平移、旋转、缩放）统一，成为连接代数与几何的桥梁。例如：

• 欧拉公式：$e^{i\theta }=\cos \theta +i\sin \theta$，揭示了指数函数与三角函数之间的深层联系，使得复数在复平面上的旋转和缩放变换可以通过指数函数来表示。

六、总结

从抽象到直观的认知跃迁，虚数的“虚”并非指“不存在”，而是人类对二维空间规律的数学抽象。从数轴到复平面的拓展，本质是认知维度的升级——正如负数曾被质疑，虚数最终通过数理自洽性与实际应用价值，成为现代科学不可或缺的工具。

拓展阅读：

• Stack Exchange 相关讨论
• A Visual Guide to Imaginary Numbers

---

via:

• GraphicMaths - i to the power i
  https://graphicmaths.com/pure/complex-numbers/i-to-power-i/

• I Power I: What Is I Raised To The Power I?
  https://www.scienceabc.com/eyeopeners/what-is-i-raised-to-the-power-i.html

• i to the i is a Real Number – Math Fun Facts
  https://math.hmc.edu/funfacts/i-to-the-i-is-a-real-number/

• 虚数的意义 - 阮一峰的网络日志 作者： 阮一峰 日期： 2012 年 9 月 24 日
  https://ruanyifeng.com/blog/2012/09/imaginary_number.html