注:本文为 “欧拉公式” 相关文章合辑。
略作重排,未整理去重。
欧拉恒等式──最优美的数学定理
Posted on 05/11/2012 by ccjou
公元 1990 年,德国 Springer Verlag 出版公司发行的 The Mathematical Intelligencer 期刊公布了一项票选结果:欧拉恒等式(Euler’s identity)获选为「最优美的数学定理」(the most beautiful theorem in mathematics)。下面抄录维基大典的欧拉生平介绍:
欧拉(Leonhard Euler),瑞士巴塞尔人,1707 年 4 月 15 日生。1726 年得博士衔。翌年,任教于俄罗斯科学院,参加俄与数学竞赛,论船桅之构作,仅败于布给。布给者,泰西航海学之父也。越四年,升任教授。复越两年,拜数学系主任。翌年,罹患,右目眇。1741 年,俄国乱,遂迁柏林,任教于柏林科学院。1766 年,返俄罗斯科学院。1783 年 9 月 18 日卒,年七十七。法兰西哲人孔多塞曰:「至此,欧拉不复算数,亦无复生也。」欧氏执十八世纪数学牛耳,论文近千,惟二十世纪保罗・艾狄胥可匹敌之。究分析,创函数,混一欧洲大陆及英国之微积分;解七桥问题,开图论及拓扑之先;论复数,究欧拉数,得欧拉恒等式,誉为最优美恒等式;论凸多面体,证欧拉等式,后人推而广之,得流形之欧拉特征值;究欧拉函数,得欧拉定理,为费马小定理之推广。
Leonhard Euler (1707 - 1783) From http://plus.maths.org/issue42/features/wilson/Euler_1_web.jpg
这是著名的欧拉恒等式:
e i π + 1 = 0 e^{i\pi} + 1 = 0 eiπ+1=0
其中 e e e 是自然对数的底数,亦称欧拉数, i i i 是虚数单位,满足 i 2 = − 1 i^2 = -1 i2=−1(或写成 i = − 1 i = \sqrt{-1} i=−1), π \pi π 是圆周率。欧拉恒等式出现了三个基本算术运算:加法、乘法与指数,联系了五个基本数学常数: 0 , 1 , e , i , π 0, 1, e, i, \pi 0,1,e,i,π。欧拉恒等式是欧拉公式(Euler formula)的一个必然结果,它说:
e i θ = cos θ + i sin θ e^{i\theta} = \cos\theta + i\sin\theta eiθ=cosθ+isinθ
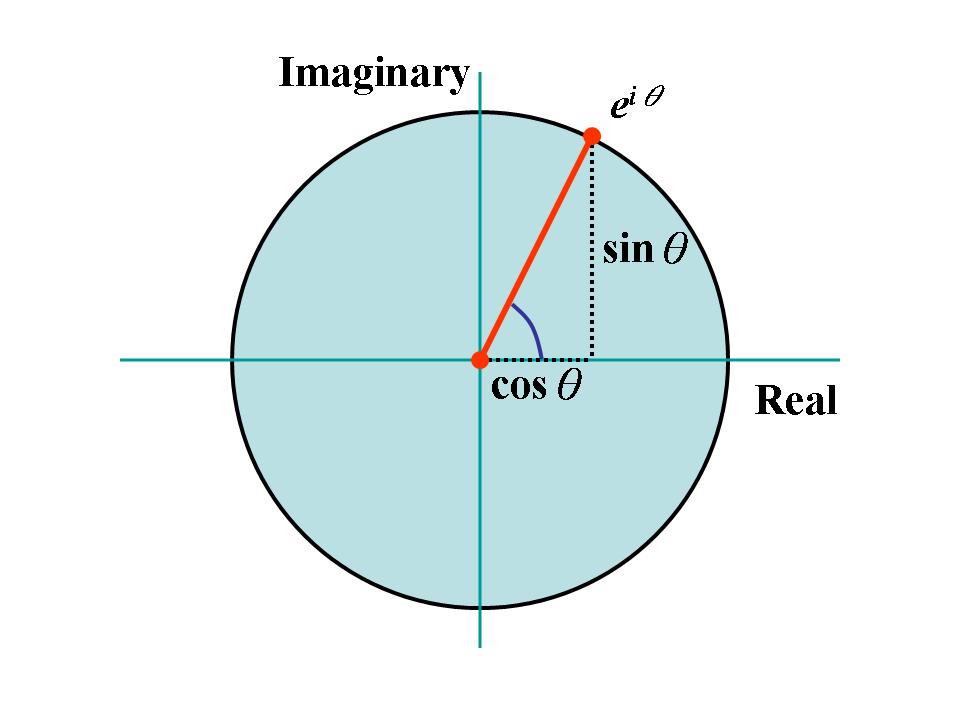
其中 θ \theta θ 为任意实数。根据欧拉公式,指数函数 e i θ e^{i\theta} eiθ 的实数部分等于余弦函数 cos θ \cos\theta cosθ,虚数部分等于正弦函数 sin θ \sin\theta sinθ。在复数平面上, e i θ e^{i\theta} eiθ 位于单位圆周, θ \theta θ 即为从 1 1 1 至 e i θ e^{i\theta} eiθ 的(有号)弧长(见图一)。当 θ = π \theta = \pi θ=π,即得欧拉恒等式。
图一 Euler’s formula
美国麻省理工学院(Massachusetts Institute of Technology,简称 MIT)斯传(Gilbert Strang)教授在他的线性代数教科书里讲述了一个关于欧拉公式证明的故事:
我还记得 MIT 收到一名纽约囚犯来信的那一天,他询问欧拉公式是否为真。当你一想到这个公式优美地将三个基础数学函数联系在一起时,不免感到惊讶。我们的最佳解答是检视幂级数
e i θ = 1 + i θ + ( i θ ) 2 2 ! + ( i θ ) 3 3 ! + ⋯ e^{i\theta} = 1 + i\theta + \frac{(i\theta)^2}{2!} + \frac{(i\theta)^3}{3!} + \cdots eiθ=1+iθ+2!(iθ)2+3!(iθ)3+⋯
其中实数部分 1 − θ 2 2 + ⋯ 1 - \frac{\theta^2}{2} + \cdots 1−2θ2+⋯ 是余弦,虚数部分 θ − θ 3 6 + ⋯ \theta - \frac{\theta^3}{6} + \cdots θ−6θ3+⋯ 是正弦。这个公式是正确的,我希望当时我们寄了一个更优美的证明。
除了 MIT 寄出的泰勒展开式(Taylor expansion)证法,我们也可以用极限定义和微分学来证明。指数函数 e x e^{x} ex 定义如下:
e x = lim n → ∞ ( 1 + x n ) n e^{x} = \lim_{n\to\infty}\left(1 + \frac{x}{n}\right)^n ex=n→∞lim(1+nx)n
代入 x = i θ x = i\theta x=iθ,并考虑数列
1 , ( 1 + i θ n ) , ( 1 + i θ n ) 2 , … , ( 1 + i θ n ) n , … 1,\left(1 + \frac{i\theta}{n}\right), \left(1 + \frac{i\theta}{n}\right)^2,\ldots,\left(1 + \frac{i\theta}{n}\right)^n,\ldots 1,(1+niθ),(1+niθ)2,…,(1+niθ)n,…
当 n → ∞ n\to\infty n→∞, ( 1 + i θ n ) n \left(1 + \frac{i\theta}{n}\right)^n (1+niθ)n 趋于 e i θ e^{i\theta} eiθ。见图二,当 n → ∞ n\to\infty n→∞, ( 1 + i θ n ) \left(1 + \frac{i\theta}{n}\right) (1+niθ) 的角度和长度分别为
∡ ( 1 + i θ n ) = θ n + o ( 1 n ) \measuredangle \left(1 + \frac{i\theta}{n}\right) = \frac{\theta}{n} + o\left(\frac{1}{n}\right) ∡(1+niθ)=nθ+o(n1)
∣ 1 + i θ n ∣ = 1 + o ( 1 n ) \left\vert 1 + \frac{i\theta}{n}\right\vert = 1 + o\left(\frac{1}{n}\right) 1+niθ =1+o(n1)
其中 o ( 1 / n ) o(1/n) o(1/n) 表示误差。所以, ( 1 + i θ n ) n \left(1 + \frac{i\theta}{n}\right)^n (1+niθ)n 从 1 1 1 启始,角度旋转了 n ∡ ( 1 + i θ n ) n\measuredangle \left(1 + \frac{i\theta}{n}\right) n∡(1+niθ),长度伸缩了 ∣ 1 + i θ n ∣ n \left\vert 1 + \frac{i\theta}{n}\right\vert^n 1+niθ n。当 n → ∞ n\to\infty n→∞,利用上面两式,可得
lim n → ∞ n ∡ ( 1 + i θ n ) = θ \lim_{n\to\infty} n\measuredangle \left(1 + \frac{i\theta}{n}\right) = \theta n→∞limn∡(1+niθ)=θ
lim n → ∞ ∣ 1 + i θ n ∣ n = 1 \lim_{n\to\infty} \left\vert 1 + \frac{i\theta}{n}\right\vert^n = 1 n→∞lim 1+niθ n=1
也就证明当 n → ∞ n\to\infty n→∞, ( 1 + i θ n ) n \left(1 + \frac{i\theta}{n}\right)^n (1+niθ)n 趋于 cos θ + i sin θ \cos\theta + i\sin\theta cosθ+isinθ。
图二 The complex number 1 + i x / n 1 + ix/n 1+ix/n
下面说明欧拉公式的微分学证法。写出 e i θ e^{i\theta} eiθ 的极坐标表达式
e i θ = r ( cos ϕ + i sin ϕ ) e^{i\theta} = r(\cos\phi + i\sin\phi) eiθ=r(cosϕ+isinϕ)
其中 r r r 与 ϕ \phi ϕ 为实数。求等号两边导数,可得
i e i θ = ( cos ϕ + i sin ϕ ) d r d θ + r ( − sin ϕ + i cos ϕ ) d ϕ d θ ie^{i\theta} = (\cos\phi + i\sin\phi)\frac{dr}{d\theta} + r(-\sin\phi + i\cos\phi)\frac{d\phi}{d\theta} ieiθ=(cosϕ+isinϕ)dθdr+r(−sinϕ+icosϕ)dθdϕ
将 r ( cos ϕ + i sin ϕ ) r(\cos\phi + i\sin\phi) r(cosϕ+isinϕ) 代回等号左边 e i θ e^{i\theta} eiθ 并整理等号右边,
− r sin ϕ + i r cos ϕ = ( cos ϕ d r d θ − r sin ϕ d ϕ d θ ) + i ( sin ϕ d r d θ + r cos ϕ d ϕ d θ ) -r\sin\phi + ir\cos\phi = \left(\cos\phi\frac{dr}{d\theta} - r\sin\phi\frac{d\phi}{d\theta}\right) + i\left(\sin\phi\frac{dr}{d\theta} + r\cos\phi\frac{d\phi}{d\theta}\right) −rsinϕ+ircosϕ=(cosϕdθdr−rsinϕdθdϕ)+i(sinϕdθdr+rcosϕdθdϕ)
比较等号两边实部和虚部,可得 d r d θ = 0 \frac{dr}{d\theta} = 0 dθdr=0 和 d ϕ d θ = 1 \frac{d\phi}{d\theta} = 1 dθdϕ=1。当 θ = 0 \theta = 0 θ=0, e i 0 = 1 e^{i0} = 1 ei0=1,可知 r ( θ ) r(\theta) r(θ) 和 ϕ ( θ ) \phi(\theta) ϕ(θ) 有初始值 r ( 0 ) = 1 r(0) = 1 r(0)=1 和 ϕ ( 0 ) = 0 \phi(0) = 0 ϕ(0)=0,合并以上结果可推论 r ( θ ) = 1 r(\theta) = 1 r(θ)=1 且 ϕ ( θ ) = θ \phi(\theta) = \theta ϕ(θ)=θ,故证得所求。
德国数学家高斯(Carl Friedrich Gauss)曾说:「如果一个学生在被告知欧拉公式时未能立刻视之为明显的事实,这个学生将来绝不会是一流的数学家。」读了 MIT 提供的证明后,那名囚犯是否因此相信欧拉公式是正确的?会不会如小说或电影情节那样,囚犯日后成为一位一流的数学家?斯传没有透露后续故事。那么听闻欧拉公式后,一般精英学者又有什么反应呢?从十九世纪美国哈佛大学数学教授皮尔斯(Benjamin Peirce)在讲堂证毕欧拉恒等式之后所说的这段话,不难想象当第一次面对史上最优美的数学定理时,多数的学生是何等茫然与困惑:
各位先生,它一定是真实的,它绝对是诡奇的。我们不了解它,我们也不明白它的含义。但我们已经证明了这个公式,所以我们知道它必定是正确的。
-
注解
-
Gilbert Strang, Linear Algebra and its Applications, third edition, Harcourt Brace Jovanovich, pp 185, 1988.
Gilbert Strang, Linear Algebra and its Applications(《线性代数及其应用》), third edition(第三版), Harcourt Brace Jovanovich(出版社), pp 185, 1988(1988年版,第185页)。
原文如下:
-
“I remember the day when a letter came to MIT from a prisoner in New York, asking if Euler’s formula was true. It is really astonishing, when you think of it, that three of the key functions of mathematics should come together in such a graceful way. Our best answer was to look at the power series e i θ = 1 + i θ + ( i θ ) 2 2 ! + ( i θ ) 3 3 ! + ⋯ e^{i\theta} = 1 + i\theta + \frac{(i\theta)^2}{2!} + \frac{(i\theta)^3}{3!} + \cdots eiθ=1+iθ+2!(iθ)2+3!(iθ)3+⋯. The real part 1 − θ 2 2 + ⋯ 1 - \frac{\theta^2}{2} + \cdots 1−2θ2+⋯ is the cosine. The imaginary part θ − θ 3 6 + ⋯ \theta - \frac{\theta^3}{6} + \cdots θ−6θ3+⋯ is the sine. The formula is correct, and I wish we had sent a more beautiful proof.”
“我记得有一天,麻省理工学院收到了一封来自纽约囚犯的信,信中询问欧拉公式是否成立。仔细想想,数学中三个核心函数竟能以如此优美的方式结合在一起,实在令人惊叹。我们给出的最佳解答是参考幂级数展开式 e i θ = 1 + i θ + ( i θ ) 2 2 ! + ( i θ ) 3 3 ! + ⋯ e^{i\theta} = 1 + i\theta + \frac{(i\theta)^2}{2!} + \frac{(i\theta)^3}{3!} + \cdots eiθ=1+iθ+2!(iθ)2+3!(iθ)3+⋯:其实部 1 − θ 2 2 + ⋯ 1 - \frac{\theta^2}{2} + \cdots 1−2θ2+⋯ 为余弦函数,虚部 θ − θ 3 6 + ⋯ \theta - \frac{\theta^3}{6} + \cdots θ−6θ3+⋯ 为正弦函数。该公式确实成立,只可惜我们没能给出一个更优美的证明。”
-
“Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don’t know what it means. But we have proved it, and therefore we know it must be the truth.”
“先生们,这无疑是正确的,它完全自相矛盾;我们无法理解它,也不知道它的含义。但我们已经证明了它,因此我们知道它必然是真理。”
Responses to 欧拉恒等式──最优美的数学定理
-
Watt Lin says:
05/13/2012 at 10:47 am
以前在一本书上,看到简洁之证明:
d z = i z d θ d z z = i d θ ∫ d z z = ∫ i d θ ln z = i θ + c z = z 0 e i θ = z 0 ( cos θ + i sin θ ) \begin{aligned} dz &= i z d\theta \\ \frac{dz}{z} &= i d\theta \\ \int \frac{dz}{z} &= \int i d\theta \\ \ln z &= i \theta + c \\ z &= z_{0} e^{i\theta} = z_{0} (\cos \theta + i \sin \theta)\end{aligned} dzzdz∫zdzlnzz=izdθ=idθ=∫idθ=iθ+c=z0eiθ=z0(cosθ+isinθ)
在书上, ( cos θ + i sin θ ) (\cos \theta + i \sin \theta) (cosθ+isinθ) 以高斯平面坐标绘图表示,而前面的微分方程,推演出圆周旋转的 e i θ e^{i\theta} eiθ。
这种证明过程,也是很有趣!
Reply
-
ccjou says:
05/13/2012 at 3:28 pm
书上说一开始 z z z 和 θ \theta θ 的关系为何?是不是 z = cos θ + i sin θ z = \cos\theta + i\sin\theta z=cosθ+isinθ?假设是这样,就有 d z d θ = − sin θ + i cos θ = i z \frac{dz}{d\theta} = -\sin\theta + i\cos\theta = iz dθdz=−sinθ+icosθ=iz,最后一个步骤取自然指数得到 z = e i θ + c = cos θ + i sin θ z = e^{i\theta + c} = \cos\theta + i\sin\theta z=eiθ+c=cosθ+isinθ,接着必须证明 c = 0 c = 0 c=0。有人可能以为令 θ = 0 \theta = 0 θ=0, e c = 1 e^{c} = 1 ec=1,故 c = 0 c = 0 c=0。但这离结果还有一段距离,因为 c c c 是复数, e c = 1 e^{c} = 1 ec=1 并不仅有唯一解 c = 0 c = 0 c=0。事实上,欧拉公式告诉我们 e c = 1 e^{c} = 1 ec=1 的解包括 c = 2 k π c = 2k\pi c=2kπ, k ∈ Z k \in \mathbb{Z} k∈Z。欧拉公式的证明重点在于釐清 exp, sin, cos 的定义,特别是复数域的定义。
说到微分方程,还有一个快捷证法。考虑 y ′ = i y y' = iy y′=iy, y ( 0 ) = 1 y(0) = 1 y(0)=1。不难确认 e i θ e^{i\theta} eiθ 和 cos θ + i sin θ \cos\theta + i\sin\theta cosθ+isinθ 都为其解,唯一性定理说明两者相等。
Reply
-
Watt Lin says:
05/13/2012 at 5:51 pm
我觉得这个证明过程很直观,尤其是通过微分方程来解释 e i θ e^{i\theta} eiθ 的旋转性质。不过,我同意您说的,证明 c = 0 c = 0 c=0 是一个关键步骤。如果能更详细地解释这一点,可能会更完美。
Reply
-
ccjou says:
05/14/2012 at 9:07 am
是的,这个证明确实很直观,尤其是对于那些熟悉微分方程的人来说。关于 c = 0 c = 0 c=0 的问题,其实可以通过考虑 e i θ e^{i\theta} eiθ 的周期性来解决。因为 e i θ e^{i\theta} eiθ 是周期为 2 π 2\pi 2π 的函数,所以 c c c 必须是一个与 θ \theta θ 无关的常数。当 θ = 0 \theta = 0 θ=0 时, e i θ = 1 e^{i\theta} = 1 eiθ=1,这自然导致 c = 0 c = 0 c=0。这种解释虽然简单,但需要对复数指数函数有更深入的理解。
Reply
-
Watt Lin says:
05/14/2012 at 10:32 am
我明白了,这种解释确实需要对复数指数函数有更深入的理解。我之前没有考虑到 e i θ e^{i\theta} eiθ 的周期性。谢谢您的详细解释,这让我对欧拉公式有了更深刻的理解。
Reply
-
-
-
-
欧拉公式的微分方程证明
一、微分方程证明的推导流程
(一)推导步骤的规范展开
基于复数域的微分关系构建推导逻辑,具体步骤如下:
- 设定复变量关系:考虑复平面上的变量
z
z
z 与实变量
θ
\theta
θ 满足微分方程
d z = i z d θ dz = iz \, d\theta dz=izdθ - 变量分离转化:将方程整理为可积分形式
d z z = i d θ \frac{dz}{z} = i \, d\theta zdz=idθ - 两端积分运算:对等式两侧分别进行不定积分
∫ d z z = ∫ i d θ \int \frac{dz}{z} = \int i \, d\theta ∫zdz=∫idθ
利用积分公式可得
ln z = i θ + c \ln z = i\theta + c lnz=iθ+c
其中 c c c 为积分常数。 - 指数化求解:对等式两边取自然指数,消去对数形式
z = e i θ + c = e c ⋅ e i θ z = e^{i\theta + c} = e^c \cdot e^{i\theta} z=eiθ+c=ec⋅eiθ
令 z 0 = e c z_0 = e^c z0=ec( z 0 z_0 z0 为非零复常数),则有
z = z 0 e i θ z = z_0 e^{i\theta} z=z0eiθ - 几何意义关联:在高斯平面中,
z
=
cos
θ
+
i
sin
θ
z = \cos\theta + i\sin\theta
z=cosθ+isinθ 表示单位圆上的复数(模长为 1,辐角为
θ
\theta
θ)。结合单位圆的约束条件,可确定
z
0
=
1
z_0 = 1
z0=1,最终得到
e i θ = cos θ + i sin θ e^{i\theta} = \cos\theta + i\sin\theta eiθ=cosθ+isinθ
(二)推导的几何直观解释
上述推导的直观性体现在:当 θ \theta θ 作为辐角连续变化时,复数 e i θ e^{i\theta} eiθ 在复平面上始终位于单位圆上,其轨迹为绕原点的圆周运动——这一“旋转性质”通过微分方程 d z d θ = i z \frac{dz}{d\theta} = iz dθdz=iz 定量描述:导数 i z iz iz 始终与 z z z 垂直(复数乘法的几何意义),确保 z z z 的模长不变,仅辐角随 θ \theta θ 线性变化。
二、推导中的关键细节与严谨性补充
(一)初始假设的合理性验证
推导隐含
z
z
z 是关于
θ
\theta
θ 的复值函数
z
(
θ
)
=
cos
θ
+
i
sin
θ
z(\theta) = \cos\theta + i\sin\theta
z(θ)=cosθ+isinθ,该假设需通过求导验证其与微分方程的一致性:
d
z
d
θ
=
−
sin
θ
+
i
cos
θ
\frac{dz}{d\theta} = -\sin\theta + i\cos\theta
dθdz=−sinθ+icosθ
利用复数运算规则,将右侧变形为
i
(
cos
θ
+
i
sin
θ
)
=
i
z
i(\cos\theta + i\sin\theta) = iz
i(cosθ+isinθ)=iz
与微分方程
d
z
d
θ
=
i
z
\frac{dz}{d\theta} = iz
dθdz=iz 完全等价,证明初始假设的合理性。
(二)积分常数 c c c 的严格确定
- 初步分析的局限性:若直接令 θ = 0 \theta = 0 θ=0,则 z ( 0 ) = cos 0 + i sin 0 = 1 z(0) = \cos0 + i\sin0 = 1 z(0)=cos0+isin0=1,代入 z = e c e i θ z = e^c e^{i\theta} z=eceiθ 得 e c = 1 e^c = 1 ec=1。但在复数域中,方程 e c = 1 e^c = 1 ec=1 的解为 c = 2 k π i c = 2k\pi i c=2kπi( k ∈ Z k \in \mathbb{Z} k∈Z),并非仅 c = 0 c = 0 c=0,需进一步排除冗余解。
- 基于微分方程解的唯一性定理:考虑初值问题
{ y ′ = i y y ( 0 ) = 1 \begin{cases} y' = iy \\ y(0) = 1 \end{cases} {y′=iyy(0)=1- 复指数函数 y 1 ( θ ) = e i θ y_1(\theta) = e^{i\theta} y1(θ)=eiθ 满足该方程: y 1 ′ = i e i θ = i y 1 y_1' = ie^{i\theta} = iy_1 y1′=ieiθ=iy1,且 y 1 ( 0 ) = 1 y_1(0) = 1 y1(0)=1;
- 三角函数组合
y
2
(
θ
)
=
cos
θ
+
i
sin
θ
y_2(\theta) = \cos\theta + i\sin\theta
y2(θ)=cosθ+isinθ 同样满足该方程(前文已验证),且
y
2
(
0
)
=
1
y_2(0) = 1
y2(0)=1。
根据线性常微分方程初值解的唯一性定理(复数域中解析函数族满足该定理), y 1 ( θ ) y_1(\theta) y1(θ) 与 y 2 ( θ ) y_2(\theta) y2(θ) 必为同一函数,故 e c = 1 e^c = 1 ec=1 中仅 c = 0 c = 0 c=0 为有效解(排除 k ≠ 0 k \neq 0 k=0 对应的周期冗余解)。
(三)周期性与推导的关联说明
e i θ e^{i\theta} eiθ 具有周期 2 π 2\pi 2π(即 e i ( θ + 2 π ) = e i θ e^{i(\theta + 2\pi)} = e^{i\theta} ei(θ+2π)=eiθ),这一性质与三角函数的周期性一致,可作为推导结果的佐证,但不能独立用于确定 c = 0 c = 0 c=0:周期性是欧拉公式的推论,而非前提,需以解的唯一性定理为依据确保推导的严谨性。
三、证明的基础定义与适用条件
(一)复数域中函数的严格定义
推导的严谨性依赖于复数域内函数的明确界定,避免依赖实数域的直观延伸:
- 复指数函数:通过幂级数定义为
e z = ∑ n = 0 ∞ z n n ! ( z ∈ C ) e^z = \sum_{n=0}^\infty \frac{z^n}{n!} \quad (z \in \mathbb{C}) ez=n=0∑∞n!zn(z∈C)
该级数在复平面上处处收敛,确保 e i θ e^{i\theta} eiθ 的解析性。 - 复三角函数:通过幂级数定义或欧拉公式反向定义:
- 幂级数定义: cos z = ∑ n = 0 ∞ ( − 1 ) n z 2 n ( 2 n ) ! \cos z = \sum_{n=0}^\infty \frac{(-1)^n z^{2n}}{(2n)!} cosz=∑n=0∞(2n)!(−1)nz2n, sin z = ∑ n = 0 ∞ ( − 1 ) n z 2 n + 1 ( 2 n + 1 ) ! \sin z = \sum_{n=0}^\infty \frac{(-1)^n z^{2n+1}}{(2n+1)!} sinz=∑n=0∞(2n+1)!(−1)nz2n+1( z ∈ C z \in \mathbb{C} z∈C);
- 反向定义: cos z = e i z + e − i z 2 \cos z = \frac{e^{iz} + e^{-iz}}{2} cosz=2eiz+e−iz, sin z = e i z − e − i z 2 i \sin z = \frac{e^{iz} - e^{-iz}}{2i} sinz=2ieiz−e−iz,与幂级数定义等价。
(二)微分方程的适用前提
复数域中,微分方程 y ′ = i y y' = iy y′=iy 解的存在性与唯一性,依赖于函数的解析性:复指数函数 e i θ e^{i\theta} eiθ 与三角函数 cos θ \cos\theta cosθ、 sin θ \sin\theta sinθ 均为复平面上的全解析函数(无奇点),满足唯一性定理的适用条件,确保推导的逻辑闭环。
四、证明方法的特征与适用场景
(一)优势特征
- 直观性强:将抽象的复指数函数与复平面上的圆周运动直接关联,帮助建立几何直觉;
- 步骤凝练:相较于幂级数展开法,无需涉及级数收敛性的复杂证明,推导流程更简洁;
- 关联紧密:建立了微分方程、复数运算与几何意义的跨知识点联系,便于系统化理解。
(二)局限性与适用前提
该方法要求学习者具备以下基础:
- 复数域的基本运算规则与几何表示;
- 不定积分的计算方法;
- 常微分方程的基本概念(尤其是解的存在性与唯一性定理);
- 复变函数的初步知识(如解析函数的定义)。
若缺乏上述基础,易忽略积分常数确定的严谨性,或难以理解微分方程与旋转性质的关联。
总结
欧拉恒等式 e i π + 1 = 0 e^{i\pi} + 1 = 0 eiπ+1=0 不仅是数学中最优美的定理之一,也是复数理论和微积分学的重要成果。通过多种证明方法,我们可以从不同角度理解这一恒等式的深刻含义。无论是在数学理论的研究中,还是在工程和物理的实际应用中,欧拉恒等式都扮演着重要的角色。
如果您对欧拉恒等式或相关数学概念有更多问题,欢迎继续讨论和交流。
正确理解欧拉公式
weixin_39851048 于 2020-11-20 00:56:39 发布
欧拉公式是数学中一个非常美丽的公式,它将五个基本数学常数联系在一起: e e e(自然对数的底), π \pi π(圆周率), i i i(虚数单位),以及整数 0 和 1。
e i π + 1 = 0 \large e^{i\pi} + 1 = 0 eiπ+1=0
笔者第一次见到这个式子是在科普读物上。当时最为困惑的一点就是, π i \pi i πi 是纯虚数, e e e 的 π i \pi i πi 次方怎么就变成了一个实数?
事实上,上面提到的公式只是原始欧拉公式的特殊情况,其原始形式如下所示。表面上看,它似乎提供了计算“纯虚数次方”的方法。要正确理解欧拉公式,就有必要先理解“虚数次方”的概念(“虚数”默认指纯虚数,下同)。
原始欧拉公式
e i x = cos x + i sin x \large e^{ix} =\cos x + i\sin x eix=cosx+isinx
一个数的“多少次方”的概念最初只对正整数幂次才有意义。 a a a 的 n n n 次方( n n n 为正整数)就是 n n n 个 a a a 相乘:
a × a × a × ⋯ × a = a n = a × a × ⋯ × a ⏟ n 个 = ∏ i = 1 n a \large a \times a \times a \times \cdots \times a = a^n = \underbrace{a\times a\times\cdots\times a}_{n\text{ 个}} = \prod_{i = 1}^{n} a a×a×a×⋯×a=an=n 个 a×a×⋯×a=∏i=1na
在不引入新定义的情况下,若 n n n 不是正整数, a a a 的 n n n 次方就无意义。例如,我们尚不明确 “-3 个 a a a 相乘” 或是 “1.23 个 a a a 相乘” 的含义。
在数学中,我们之所以能计算非整数次方,是因为人们对定义做了拓展,这带有人为规定的性质。当然,拓展遵守一个原则:尽量使拓展前的数学性质在拓展后仍适用,类似于软件的“前向兼容性”。此外,作为新定义,拓展必须建立在已有的定义上,否则就会有模糊性。
作为例子,我们来看看 “ a a a 的 n n n 次方”(简记为 a n a^n an)中 n n n 是如何拓展到负整数的: n n n 为负整数时,记 n n n 的绝对值为 ∥ n ∥ \| n \| ∥n∥,则 a n a^n an 等于 a ∥ n ∥ a^{\| n \|} a∥n∥ 再取倒数。这一拓展满足“前向兼容性”,例如:
( a n ) × ( a m ) = a n + m \large (a^n) \times (a^m) = a^{n+m} (an)×(am)=an+m
这个性质在拓展后仍适用;拓展中的绝对值、倒数运算都是已定义的,没有模糊性。这样看,这个拓展是非常自然的。最终,我们把 n n n 推广到了任意实数 x x x。
那么,我们能否把实数 x x x 拓展到虚数情况?为了契合主题,这里只考虑 e x e^x ex。要以“较为自然”的方式把 x x x 拓展到虚数,可以考察 e x e^x ex 的幂级数形式,如下:
e x = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + ⋯ \large e^x = 1 + x +\frac{x^2}{2!} +\frac{x^3}{3!} +\frac{x^4}{4!}+\cdots ex=1+x+2!x2+3!x3+4!x4+⋯
似乎把上式的 x x x 简单代换为 i x ix ix,拓展工作就完成了。但要注意的是, e x e^x ex 原本是定义在 x x x 为实数的情况下,因此上式只对实数情况适用,把 x x x 简单替换为 i x ix ix 得到的“等式”必须理解为仿照 e x e^x ex 幂级数形式人为规定的定义式。
e i x = def 1 + i x + ( i x ) 2 2 ! + + x 4 4 ! + ( i x ) 3 3 ! + ⋯ \large e^{ix}\stackrel{\text{def}}{=} 1 + ix +\frac{(ix)^2}{2!} ++\frac{x^4}{4!}+\frac{(ix)^3}{3!} +\cdots eix=def1+ix+2!(ix)2++4!x4+3!(ix)3+⋯
我们特别在等号上加 “ d e f def def” 以强调它是定义式。我们可以把等号右边每一项计算出来,然后把实数部分和虚数部分各自合并,如下。
e i x = def ( 1 − x 2 2 ! + x 4 4 ! − ⋯ ) + i ( x − x 3 3 ! + x 5 5 ! − ⋯ ) \large e^{ix} \stackrel{\text{def}}{=} \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \right) + i \left(x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \right) eix=def(1−2!x2+4!x4−⋯)+i(x−3!x3+5!x5−⋯)
↑↑ e i x \large e^{ix} eix 正式定义
我们把上式作为 e 的虚数次方 的正式定义。它的右边只涉及乘除运算、正整数次方以及无穷级数求和,因此建立在已有定义上。定义式中括号部分刚好就是余弦、正弦函数的级数形式,从而自然地导出了欧拉公式!利用这点,我们可以证明仍有:
e i x × e i y = e i x + i y \large e^{ix}×e^{iy}=e^{ix+iy} eix×eiy=eix+iy
因此这个定义也满足一定 “兼容性”。

根据这些讨论,欧拉公式是
e
i
x
\large e^{ix}
eix 的定义式的简单推论。不难看出,
e
e
e 的 “虚数次方” 与
e
e
e 的实数次方在定义上有很大差别。
此外,“虚数次方”与实数次方并不是完全兼容,比方说,实数情况下有
a ≠ b \large a \neq b a=b ,
就一定有
e a ≠ e b \large e^a \neq e^b ea=eb,
这个性质在虚数情况下不适用,一个简单例子是:
e π i = e 3 π i \large e^{\pi i} = e^{3\pi i} eπi=e3πi
因此,“虚数次方” 并不是好的说法, e i x \large e^{ix} eix 只是一个形式记号。
在一定意义上, e i x \large e^{ix} eix 是 c o s x + i s i n x \large cosx+isinx cosx+isinx 的简便记法。
Euler Formula(欧拉公式)推导
越来越胖的 GuanRunwei 已于 2023-12-20 15:20:34 修改
导语
不论是高等数学还是大学物理,欧拉公式都如影随形。因为其重要性和划时代意义,Euler Formula (欧拉公式)有着很多了不起的别称,例如“上帝公式”、“最伟大的数学公式”、“数学家的宝藏”等等。

欧拉公式在数学、物理和工程领域应用广泛。物理学家理查德·费曼 (Richard Phillips Feynman) 将欧拉公式称为:“我们的珍宝”和“数学中最非凡的公式”。
法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon marquis de Laplace)曾这样评价欧拉对于数学的贡献:“读欧拉的著作吧,在任何意义上,他都是我们的大师”。
这个发表于公元1748年的数学公式,将三角函数与复指数函数巧妙地关联了起来。
e i x = cos x + i sin x {{e}^{ix}}=\cos x+i\sin x eix=cosx+isinx
其中, e e e 为自然常数, i i i 为虚数, x x x 则是以弧度为单位的参数(变量)。
尤其是当参数 x x x 等于 π \pi π 的时候,欧拉公式可简化为:
e i π + 1 = 0 {{e}^{i\pi }}+1=0 eiπ+1=0
上式将 5 个微妙且看似无关的数学符号 e , i , π , 0 , 1 e, i, \pi, 0, 1 e,i,π,0,1 紧密地联系起来,其美妙之处让人称绝。
推导
开头介绍了欧拉公式的一种通用写法是:
e i x = cos x + i sin x {{e}^{ix}}=\cos x+i\sin x eix=cosx+isinx
其将复指数与正弦、余弦函数联系了起来。那么这是如何做到的?能否更加直观一点呢?
通常书本上给出的都是欧拉公式的验证而不是推导,例如,很多人会说:只要分别将两边的自然指数函数和三角函数用泰勒级数展开,即可得出两边相等的结论,但这只是验证而非真正的推导,就连《费曼物理学讲义》里面的计算也是如此。
为了让其更加易于理解,这里试着用直观的方式给予推导!
首先,需要记住的一点是:Euler 方程等号两边都可以看作是描述在一个圆上的位置或者运动。
如果我们用三角函数去描述圆心在复平面原点处的单位圆上的位置或圆周运动轨迹,当圆弧角为 x x x 弧度时,如图有:
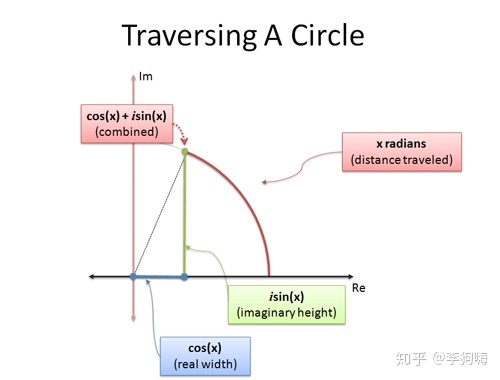
c o s ( x ) cos(x) cos(x) :当前圆周运动位置的横坐标
s i n ( x ) sin(x) sin(x):当前圆周运动位置的纵坐标
因此,采用复数 c o s ( x ) + i s i n ( x ) cos(x) + isin(x) cos(x)+isin(x) ,即可描述单位圆周上点的位置或运动轨迹。
用复数来描述坐标傻子都能理解,那么欧拉公式左边的复指数又代表什么呢?(由于欧拉公式左边复指数中的实部为零,只包含虚部,因此也可以称之为虚指数)
先举个实指数相关的例子,当看到 3 4 3^4 34 时,你可以把它看做4个3连乘,但也可以换一个角度看。因为作为底数来说, e e e 作为自然底数,是所有连续复利增长过程都共有的基本属性,其内涵是单位数量在经过单位时间增长率为100%的连续复利增值后的最终结果。
我们可以将 3 4 3^4 34 改写为 e l n ( 3 ) ⋅ 4 e^{ln(3)\cdot 4} eln(3)⋅4 ,其数学内涵可以解释为:单位数量在单位时间增长率为 l n ( 3 ) ln(3) ln(3) 的连续复利情况下,经过 4 个单位时间增长后的最终结果。
通式可以写为: Q = e r a t e ⋅ t i m e Q = e^{rate\cdot time} Q=erate⋅time
其中, r a t e rate rate 表示单位时间的增长率, t i m e time time 表示经历了多少个单位时间的增长,而 Q Q Q 表示最终增长结果是初始值的多少倍。
因此,跳开数值本身的大小问题,我们把“乘以实指数”看成是一种“增长”或者说是对初始值的一种“推动”作用(这里初始值是具有大小和方向属性的“复数”,复数包含实数和虚数,表达式可写为:复数 = 实部 + i i i 虚部)。
再例如实数 3 3 3,可将其看做是:单位时间增长率为 l n ( 3 ) ≈ 1.1 ln(3)\approx 1.1 ln(3)≈1.1,初始值以该增长率连续复利增长,经过单位时间后最终结果将是 e l n ( 3 ) ⋅ 1 = 3 e^{ln(3) \cdot 1} =3 eln(3)⋅1=3。
这里先只考虑了增长率为实数时的增长作用,而以实数为增长率的这种“增长”或“推动”是沿着初始值方向进行的(复数可以看做是复平面上的矢量,因此具有方向属性)。

而虚指数所带来的增长作用就和实指数有所不同,虚指数的增长作用的方向与初始值的方向垂直,且随着数值的变化始终保持着这种垂直的关系。
这种增长方式并不改变数的大小,而只改变复数的方向!例如,让任何数乘以虚数 i i i,都不会改变数的大小(或增长),而是改变数的方向。
在《自然底数 e e e 怎么就“自然”了?》中已经给出了自然底数 e e e 的定义式:
e = lim n → ∞ ( 1 + 1 n ) n = lim n → ∞ ( 1 + 100 % n ) n e=\lim\limits_{n \to \infty}\left(1+\frac{1}{n}\right)^{n}=\lim\limits_{n \to \infty}\left(1+\frac{100\%}{n}\right)^{n} e=n→∞lim(1+n1)n=n→∞lim(1+n100%)n
不过在上式中,我们假设的增长率为实数,但是,如果增长率为虚数呢?
e i = lim n → ∞ ( 1 + 100 % ⋅ i n ) n e^{i}=\lim\limits_{n \to \infty}\left(1+\frac{100\% \cdot i}{n}\right)^{n} ei=n→∞lim(1+n100%⋅i)n
其增长的示意图如下图所示:
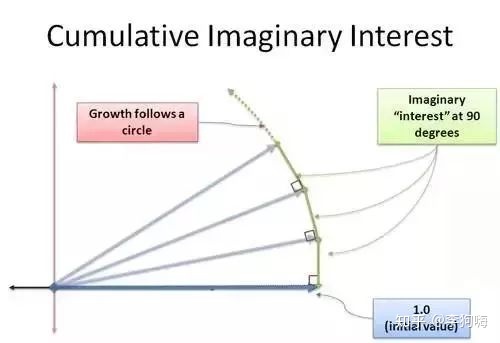
现在,“新的增长率”其实一直是沿着复数的垂直方向。并且这并不会改变复数的长度,但有人会提出质疑,因为上图所示的示意图是由一个个直角三角形组成,斜边当然比直角边更大。
但要知道,我们正在处理的是一个极限问题,当 n → ∞ n \rightarrow \infty n→∞(其实 n n n )可以看作到达最后结果所经历的增长步数,这个增长步数是我们人为设定的,上图中每个绿色的直角边都代表一步),则绿色的直角边将越接近斜边。
最终将得到的结果是:复数长度(模长)不变的连续旋转。这是处理其与正弦、余弦之间关系的核心概念,当复数的增量始终与复数的方向保持垂直,得到的轨迹必将是一个圆!
下面用公式来证明这一过程:
e i = lim n → ∞ ( 1 + 100 % ⋅ i n ) n \large e^{i}=\underset{n\to\infty}{\lim}\left(1 + \frac{100\% \cdot i}{n}\right)^{n} ei=n→∞lim(1+n100%⋅i)n
复数的模长为实部平方与虚部平方的和的平方根;转角为虚部除以实部的反正切值。
对于上式,如果 n = 1 n=1 n=1,则结果为 1 + i 1+i 1+i;(注意复数的运算法则是:所有模长增量相乘得到最终模长;所有转角增量相加得到最终转角) img
- 模长增量: 1 2 + 1 2 \sqrt{1^{2}+1^{2}} 12+12
- 最终模长: 1 2 + 1 2 \sqrt{1^{2}+1^{2}} 12+12
- 转角增量: arctan ( 1 1 ) \arctan(\frac{1}{1}) arctan(11)
- 最终转角:
arctan
(
1
1
)
\arctan(\frac{1}{1})
arctan(11)

如果上式中 n = 2 n=2 n=2,则结果为 ( 1 + i 2 ) 2 (1 + \frac{i}{2})^2 (1+2i)2;img
- 模长增量: 1 2 + ( 1 2 ) 2 \sqrt{1^{2}+(\frac{1}{2})^{2}} 12+(21)2
- 最终模长: ( 1 2 + ( 1 2 ) 2 ) 2 {{\left( \sqrt{{{1}^{2}}+{{\left( \frac{1}{2} \right)}^{2}}} \right)}^{2}} (12+(21)2)2
- 转角增量: arctan ( 1 2 ) \arctan(\frac{1}{2}) arctan(21)
- 最终转角: 2 arctan ( 1 2 ) 2\arctan(\frac{1}{2}) 2arctan(21)
即,将 n = 1 n=1 n=1 的一步完成增长变为了 n = 2 n=2 n=2 的两步完成增长。
那么当 n → ∞ n \rightarrow \infty n→∞ 时,分步增长就变成了连续增长问题;img
- 模长增量: lim n → ∞ 1 2 + ( 1 n ) 2 = 1 \lim\limits_{n \to \infty} \sqrt{1^{2}+(\frac{1}{n})^{2}} = 1 n→∞lim12+(n1)2=1
- 最终模长: lim n → ∞ ( 1 2 + ( 1 n ) 2 ) n = lim n → ∞ ( 1 + 1 n 2 ) n 2 1 2 n = lim n → ∞ e 1 2 n = 1 \lim\limits_{n \to \infty}\left(\sqrt{1^{2}+(\frac{1}{n})^{2}}\right)^{n}=\lim\limits_{n \to \infty}(1+\frac{1}{n^{2}})^{n^{2}\frac{1}{2n}}=\lim_{n \to \infty}e^{\frac{1}{2n}} = 1 n→∞lim(12+(n1)2)n=n→∞lim(1+n21)n22n1=limn→∞e2n1=1
- 角度增量: lim n → ∞ arctan ( 1 n ) = 1 n \lim\limits_{n \to \infty} \arctan(\frac{1}{n})=\frac{1}{n} n→∞limarctan(n1)=n1
- 最终角度: lim n → ∞ n ⋅ arctan ( 1 n ) = 1 \lim\limits_{n \to \infty} n\cdot\arctan(\frac{1}{n}) = 1 n→∞limn⋅arctan(n1)=1
实际上就是复数 1 + i ⋅ 0 1+i\cdot0 1+i⋅0 逆时针旋转,每一小步的增长方向都和复数指向方向垂直,且保证模长不变,因此极限状态就是圆周运动,最后转动角度为 1 1 1 弧度。
即 e i = c o s 1 + i ⋅ s i n 1 e^i = cos1+i \cdot sin1 ei=cos1+i⋅sin1。
那对于更为普遍的 e x i e^{xi} exi 呢?当 n → ∞ n \rightarrow \infty n→∞ 时:img
- 模长增量: lim n → ∞ 1 2 + ( x n ) 2 = 1 \lim\limits_{n \to \infty} \sqrt{1^{2}+(\frac{x}{n})^{2}} = 1 n→∞lim12+(nx)2=1
- 最终模长: lim n → ∞ ( 1 2 + ( x n ) 2 ) n = lim n → ∞ ( 1 + x 2 n 2 ) n 2 x 2 x 2 2 n = lim n → ∞ e x 2 2 n = 1 \lim\limits_{n \to \infty}(\sqrt{1^{2}+(\frac{x}{n})^{2}})^{n}=\lim\limits_{n \to \infty}(1+\frac{x^{2}}{n^{2}})^{\frac{n^{2}x^{2}}{x^{2}2n}}=\lim_{n \to \infty}e^{\frac{x^{2}}{2n}} = 1 n→∞lim(12+(nx)2)n=n→∞lim(1+n2x2)x22nn2x2=limn→∞e2nx2=1
- 角度增量: lim n → ∞ arctan ( x n ) = x n \lim\limits_{n \to \infty} \arctan(\frac{x}{n})=\frac{x}{n} n→∞limarctan(nx)=nx
- 最终角度: lim n → ∞ n ⋅ arctan ( x n ) = x \lim\limits_{n \to \infty} n\cdot\arctan(\frac{x}{n}) = x n→∞limn⋅arctan(nx)=x
实际上也是复数 1 + i ⋅ 0 1+i\cdot0 1+i⋅0 逆时针不断旋转,每一小步的转动方向都和复数指向方向垂直,且保证模长不变,因此极限状态也是圆周运动,所以当然可以用欧拉公式等号右边三角函数法定义的单位圆周上的点来完全等效(注意,这里的 x x x 都采用弧度制)。
即 e x i = c o s x + i s i n x e^{xi} = cosx+isinx exi=cosx+isinx
如果 x x x 是随时间线性变化的参数,则可以得到以下三维等径螺旋线,该螺旋线在复平面上的投影是一个圆,投影点在圆上的运动为匀速圆周运动。
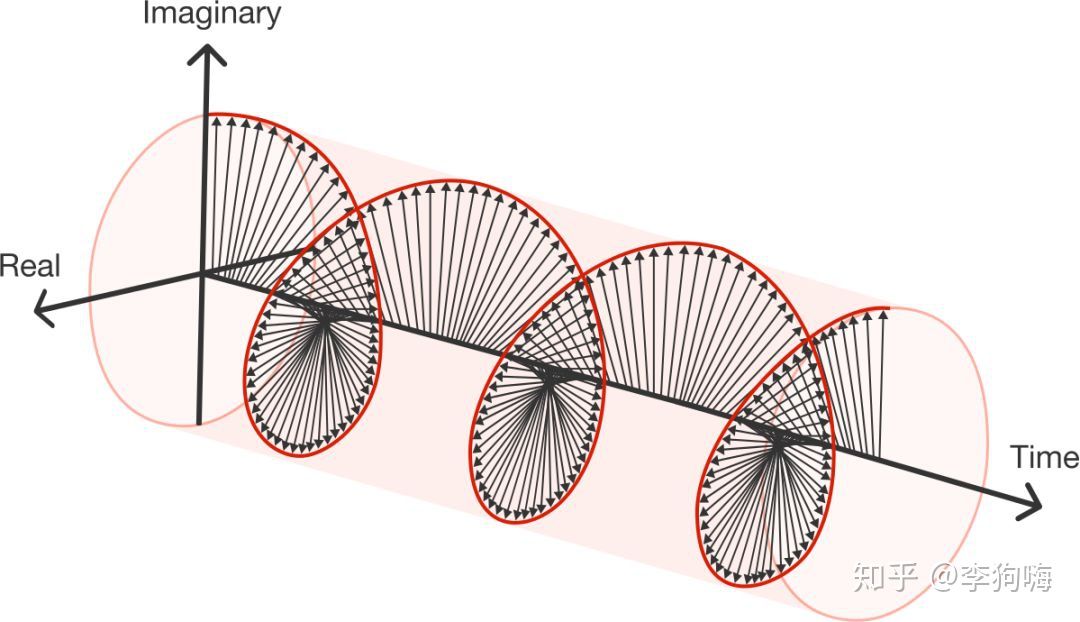
这里只要令 x = π x=\pi x=π ,就有 e π i = c o s π + i ⋅ s i n π = − 1 e^{\pi i} = cos\pi + i\cdot sin\pi = -1 eπi=cosπ+i⋅sinπ=−1 或者 e π i + 1 = 0 e^{\pi i}+1=0 eπi+1=0
推导完毕。
篇外
“数学之王” 传奇:有数字的地方就有欧拉
原创 科学方程式
“走,去柏林。”
1741 年 6 月 19 日,初夏的圣彼得堡乍暖还寒,接到柏林普鲁士腓特烈大帝亲笔邀请信的莱昂哈德・欧拉(Leonhard Euler),终于下定决心,携家人一道启程前往柏林。这一去,就是 25 年,欧拉将其数学生涯中最辉煌的一段时间留在了日耳曼的国度中。
回顾欧拉的一生,虽然他生于瑞士,但其学术生涯是从圣彼得堡全面开始,进而在柏林成就了一代数学大师的地位,暮年他重返圣彼得堡,并最终长眠于此。
两百年多后的今天,当我们再次审视腓特烈大帝的那次 “挖人才” 行为,发现他不仅为柏林科学院请来了 “数学担当”,更成就了一名数学天才向科学巨匠的华丽转变。那一天,不仅对欧拉个人意义重大,也影响了整个科学界的发展。
01 巴塞尔:数学天才的成长之路
1707 年 4 月,瑞士巴塞尔城一个牧师家庭欣喜地迎来了一名小男孩,曾在巴塞尔大学就读的父亲为其取名为:莱昂哈德・欧拉。
9 岁的欧拉就开始阅读牛顿著名的《自然哲学的数学原理》,十岁时,欧拉自学《代数学》。13 岁时他考入名校巴塞尔大学主修哲学和法律,成为不折不扣的 “少年大学生 “,年轻的他还偷偷跑去听数学课。
当时主讲数学的老师是约翰・伯努利 (Johann Bernoulli),发现欧拉的数学天赋后约定每周单独给他上数学课。时间一长,约翰・伯努利就问欧拉,你数学这么好,为啥不来数学系呢?受到鼓励后的欧拉立即师从约翰・伯努利学习数学。
伯努利家族是当时世界著名的数学世家
欧拉是大学里年龄最小的学生,还是升级最快的学生,1726 年就获得硕士学位,同年欧拉发表《论桅杆配置的船舶问题》引起学术界的关注,并因此获得当时世界学术中心 —— 巴黎学院的资助。
他异于常人的智慧,令人叹服的记忆力,不仅帮助他在数学领域一飞冲天,更为后来全领域的科学探索奠定了坚实的基石。
02 圣彼得堡:辉煌数学之旅的开端
在 18 世纪,欧洲许多国家非常重视科学和人才的作用。1725 年,俄国成立皇家科学院(即圣彼得堡科学院),彼得大帝不惜重金聘请全世界优秀的科研人才加入。此时,约翰・伯努利的两个儿子都加入了圣彼得堡科学院,其中丹尼尔・伯努利也向欧拉伸出橄榄枝,邀请他到俄国皇家科学院工作。
1727 年,年仅 20 岁的欧拉带着对数学的无限热爱离开瑞士踏上了前往俄国的行程,在圣彼得堡,欧拉辉煌的数学之旅正式开启。
在圣彼得堡的 14 年间,欧拉发表的多篇数学论文都在数学界都引起了极大震动,其中对巴塞尔问题 (Basel Problem)、哥尼斯堡七桥问题的研究更是让其名声大噪。
巴塞尔问题的精妙解法
意大利数学家彼得罗・门戈利于 1650 年提出巴塞尔问题,这个问题难倒了上百位数学家。1734 年,欧拉给出了巴塞尔问题的精妙解法,让他由此享誉整个欧洲。
巴塞尔问题是求自然数的平方倒数之和的精确值:
∑ n = 1 ∞ 1 n 2 = 1 1 2 + 1 2 2 + 1 3 2 + … \large\displaystyle\sum\limits_{n=1}^{\infty }{\frac{1}{\mathop{n}^{2}}}=\frac{1}{\mathop{1}^{2}}+\frac{1}{\mathop{2}^{2}}+\frac{1}{\mathop{3}^{2}}+\ldots n=1∑∞n21=121+221+321+…
欧拉的独到见解是将 sinc ( π x ) \displaystyle\text{sinc}(\pi x) sinc(πx) 函数写成了根式解的形式,并将有限多项式的观察推广到无穷级数,由此推导出巴塞尔问题的准确值是 π 2 6 \displaystyle\frac{\pi^{2}}{6} 6π2。
sinc ( π x ) = sin ( π x ) π x \large\displaystyle\text{sinc}(\pi x)=\frac{\sin(\pi x)}{\pi x} sinc(πx)=πxsin(πx)
图论、拓扑学、欧拉乘积公式等创新
1735 年,欧拉以其惊人的才智,用时三天计算出一个曾困扰天文学家数月的难题 —— 彗星轨道的计算。接下来一年,欧拉发表了论文《哥尼斯堡的七座桥》,从而开创了数学的一个新分支:图论和几何拓扑。那一年,欧拉年仅 29 岁。
一直到 1737 年,欧拉创新的步伐并未停歇,发表欧拉乘积公式,其对数论、复变函数以及素数分布、黎曼 ζ 函数等领域产生了深远的影响。
-
欧拉乘积公式
ε ( z ) = ∏ p 1 1 − p − z \large\varepsilon(z)=\prod_{p} \frac{1}{1 - p^{-z}} ε(z)=∏p1−p−z1, p p p 为素数, z ∈ C z\in C z∈C。
-
黎曼 ζ 函数
ζ ( z ) = ∑ n = 1 ∞ 1 n z \large\zeta(z)=\sum_{n = 1}^{\infty} \frac{1}{n^{z}} ζ(z)=∑n=1∞nz1
-
黎曼和 - 欧拉积等值定理
ζ ( z ) = ε ( z ) \large\zeta(z)=\varepsilon(z) ζ(z)=ε(z),即
∑ n = 1 ∞ 1 n z = ∏ p 1 1 − p − z \large\sum_{n = 1}^{\infty} \frac{1}{n^{z}}=\prod_{p} \frac{1}{1 - p^{-z}} ∑n=1∞nz1=∏p1−p−z1
1735 年,欧拉为协助地理所编制当时俄国的第一张全境地图,投入了极大精力和细致专注,以至于连续多日的劳累使他高烧不退,最终导致右眼失明。
03 柏林篇章:最美公式铸就数学传奇
尽管在圣彼得堡的成就蒸蒸日上,但俄国内部的权力之争愈演愈烈,此时已结婚生子的欧拉,为避免打压和迫害,内心萌生了离开彼得堡的想法。
受普鲁士国王腓特烈大帝的邀请,1741 年 6 月 19 日,34 岁的欧拉携带家人跨越国界来到柏林科学院,开启了学术生涯的新篇章。25 年的柏林岁月里,欧拉用他近 400 篇论文奠定了其最伟大数学家之一的地位。
1748 年,欧拉出版了一生中影响最大的两本数学专著,一本是关于函数的《无穷小分析引论》。
该书给出了著名的极限公式:
e = lim n → ∞ ( 1 + 1 n ) n \large e=\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^{n} e=limn→∞(1+n1)n
当 𝑛 趋向于无穷大时,e 就是一个非常重要的数学常数,大约等于 2.71828…
而复变函数论里的欧拉公式
e i θ = cos θ + i sin θ \large {{e}^{i\theta }}=\cos \theta +i\sin \theta eiθ=cosθ+isinθ
更是在微积分教程中占据了重要地位。这个公式把微积分的三个极为重要的函数联系在了一起,这些函数成为后代学者们研究了几百年的课题。

另一本则是更为著名的《微分学原理》。在这本书里,欧拉用形式化方法把微积分从几何中解放出来,使其建立在算术化与代数的基础之上,对函数及微分学发展做出极为重要的贡献:
1) 给出了基于量的代数关系下的函数的新定义,并引进现在普遍使用的函数符号;
2) 提出代数函数与超越函数的概念,定了多元函数,并对显函数和隐函数,单值函数与多值函数进行区分;
3) 建立了三角函数与指数函数之间的关系;
4) 首创了对数函数 l o g x logx logx 与 e e e 的现代讲法,并发现 logx 是无穷多值;
5) 提出二阶偏导数的演算,给出了 z / x y = z / y x z/xy=z/yx z/xy=z/yx 成立的条件;
6) 研究二元函数极值,给出了全微分的可积条件;
7) 区分了函数的增量与函数的微分;
8) 把导数作为微积分的基本概念。
由于理念过于超前,欧拉在柏林出版的这些书籍长期以来被作为欧洲学院数学的必学教材。
欧拉发明并在这些书中使用的符号 —— 圆周率的符号 π、函数符号 f (x)、以及三角学符号 sin、cos、tg 等等,成为了全世界通用的数学符号。这或许连欧拉本人都没有想到。
除了出版这两本名著,欧拉在柏林最 “出圈” 的科学研究成果则是其于 1748 提出的 “欧拉恒等式”。
欧拉恒等式将数学中几个看似不相关的常数 —— 自然对数底 e、圆周率 π、虚数单位 i、以及整数 1 和 0,以一种令人难以置信的简洁方式联系起来,它以一种几乎魔法般的方式,将数学中最基本的常数编织在一起,揭示了宇宙秩序的内在和谐。这样简短的公式蕴含了深刻的意义,展示了数学结构的精妙和谐。欧拉恒等式被公布以来,人们丝毫不吝惜溢美之词,将 “上帝赐予的公式”、“人类最美丽的公式” 这些赞美送给了欧拉。
e i π + 1 = 0 \large {{e}^{i\pi }}+1=0 eiπ+1=0
除了具有简洁的形式之美外,欧拉恒等式还为数论和数学分析之间搭建了桥梁,从而使微积分等工具能够应用于数论的研究领域。这让欧拉成为解析数论的重要奠基人之一。1859 年,著名数学家高斯的学生黎曼将欧拉恒等式推广到复数,并提出了黎曼 ζ 函数零点分布的猜想(黎曼猜想),至今仍是数学界未解的重大难题之一。
04 重返圣彼得堡:暮年的辉煌与遗产
岁月流转,1762 年俄国新女皇叶卡捷琳娜二世继位,她非常仰慕欧拉的学术成就。1766 年,年逾 60 的欧拉应叶卡捷琳娜二世之邀重返寒冷的圣彼得堡。尽管视力日渐衰退,他对数学以及物理等多个学科的研究反而愈发勤奋与深刻。
在重返圣彼得堡不久后,欧拉彻底失明,但他凭借超强的记忆力和心算能力,用口述的方式继续以平均每周一篇的速度发表论文。
在 1768 年到 1770 年之间,欧拉发表了他人生中最重要三本书的最后一本《积分学原理》。他把前人的发现加以总结并注入自己的见解,书中包含了欧拉对于积分数学的深度研究内容,还展示了他在常微分方程和偏微分方程理论方面的众多发现。后世数学家评论,《积分学原理》的出版标志着欧拉将牛顿和莱布尼茨发明的微积分方法,推向了新的高度。
欧拉出版《无穷分析引论》(1748)、《微分学》(1755) 和《积分学》(共三卷,1768-1770) 三本书,堪称微积分发展史上里程碑式的著作,在很长时间内一直被作为分析课本的典范在全世界使用。
与在柏林不断地发表原创性成果不同,欧拉第二次返回圣彼得堡后,还凭借一己之力改变了俄国落后的数学研究状况。欧拉在俄国的 31 年里,还为俄国编写了初等数学教程,帮助改革度量衡制度,设计计算税率、年金和养老保险等的公式,他为俄罗斯数学的全面崛起奠定了坚实的基础。在欧拉离世 80 年后,圣彼得堡科学院竟然还在出版他撰写的论文。
1911 年,彼得堡科学院开始整理出版欧拉的著作《欧拉全集》,这是对这位数学巨人学术遗产的全面梳理。目前已出版 80 余卷,还尚未完成此项任务。这个耗费了将近一个世纪时间的庞大的出版项目,充分证明了欧拉与生俱来的过人数学天赋。
05 欧拉已逝,精神永存:数学可以让生活更美好
1783 年 9 月 18 日,欧拉一边喝着茶,一边给小孙女讲解天王星运算轨道的数学计算。突然之间,烟斗从他手中掉了下来。他说了一句 “我死了”,随即欧拉 “停止了生命和计算”,人们在悲痛中与这位伟大的数学巨匠告别。
回顾欧拉光辉的一生,他不仅用自己的天赋和勤奋,将数学在理论上推向了新的高度,更用自己实际行动证明了 “数学可以让生活更美好。” 他用数学设计轮船,启动了波浪动力学。他用数学研究耳朵,探索声波的秘密。他用数学来测量,整合了平面测量学。他用数学算渠道断面,开启了应用流体力学。他用数学来算保险,精准货币,产生了计量经济学。他又用数学算老鹰的飞翔,建立了航空动力学。
欧拉已逝,精神永存。站在欧拉的肩膀上,欧洲又相继诞生了高斯、拉格朗日等伟大的数学巨匠,他们用手中的笔,剥开 “数学王国” 的重重迷雾,引导人类孜孜以求地从自然的不确定性中找寻确定性,人类迎来了数学的 “黄金时代”。
有数字的地方就有欧拉。

参考资料:
- On the Beauty of Math. The Great Mathematician Euler and History| by Marco Tavora Ph.D. | Towards Data Science
https://towardsdatascience.com/on-the-beauty-of-math-f2453be9db84
科普篇:史上最美数学公式 —— 欧拉恒等式

这个公式一共包含 5 个常数与 2 个符号,全都是构成数学的最基本要素,以极其简洁的形式结合在一起。
0 和 1 是最简单的两个实数,也是构造代数的基础,有了它们就可以得到其他任何数字。 任何数与 0 相加等于它本身,任何数与 1 相乘也等于它自身,因此它们也是抽象代数中群、环、域的基本元素。
圆周率 π π π,隐藏着世界上最完美的平面对称图形 —— 圆。 它代表着人类自古以来对数与形的探索,是几何与三角函数的基础。
自然常数 e e e 与微积分相伴而生。 它是微积分与概率论的化身,代表着与工业革命相适应的数学。
虚数单位 i i i,是 − 1 - 1 −1 的平方根,有了它就有了虚数、平面向量与四元数,也因此构成了电子学与量子力学的理论基础。
“ + + +” 是最基础的运算符号,减法是加法的逆运算,乘法是累计的加法,有了加法就能引申出其余的运算。
“ = = =” 是最基本的关系符号,它代表了世上最重要的关系 —— 平衡。
这就是最美公式的构成。
它诞生于群星璀璨的时代,与微积分的发展密不可分。

牛顿和莱布尼茨发明了微积分,但当时的微积分还只是个孩童,真正拉扯它长大成人的,是四大数学家之一的欧拉。正因如此,欧拉也被称为 “分析的化身”。
雅各布・伯努利在研究复利问题时,首先提出了著名的极限,而后,欧拉将其推广,并将该常数命名为 e,也就是自然常数。
艾萨克·牛顿(Isaac Newton,1643年1月4日-1727年3月31日),爵士,英国物理学家、数学家、哲学家。
戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz,1646年7月1日-1716年11月14日),德国哲学家、数学家,是历史上少见的通才,被誉为十七世纪的亚里士多德。
莱昂哈德·欧拉(Leonhard Euler,1707年4月15日—1783年9月18日),瑞士数学家、自然科学家。
雅各布·伯努利(Jakob Bernoulli,1654-1705年),伯努利家族代表人物之一,瑞士数学家。被公认的概率论的先驱之一。他是最早使用“积分”这个术语的人,也是较早使用极坐标系的数学家之一。还较早阐明随着试验次数的增加,频率稳定在概率附近。他还研究了悬链线,还确定了等时曲线的方程。概率论中的伯努利试验与大数定理也是他提出来的。
指数函数 e x e^{x } ex 成为了微积分中最重要的函数,没有之一,因为它是唯一一个(不考虑常数倍)导数和积分都是其自身的函数。
紧随其后的就是余弦函数 c o s x cosx cosx 和正弦函数 s i n x sinx sinx 。
在泰勒公式的加持下,三个函数都有优美的级数展开形式:
e x = 1 + x 1 ! + x 2 2 ! + x 3 3 ! + … \large e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots ex=1+1!x+2!x2+3!x3+…
cos x = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + … \large \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots cosx=1−2!x2+4!x4−6!x6+…
sin x = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + … \large \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots sinx=x−3!x3+5!x5−7!x7+…
布鲁克·泰勒(Brook Taylor,1685年8月18日-1731年12月29日)英国数学家,他主要以泰勒公式和泰勒级数闻名。
将它们联系起来,就得到了欧拉公式:img
欧拉公式推导
一、麦克劳林级数基础
麦克劳林级数是函数在 x = 0 x = 0 x=0 处的泰勒级数展开形式。以下三个函数的麦克劳林级数是后续推导的重要基础:
- 指数函数 e x e^x ex 的麦克劳林级数:
e x = ∑ n = 0 ∞ x n n ! = 1 + x 1 ! + x 2 2 ! + x 3 3 ! + x 4 4 ! + ⋯ e^x=\sum_{n = 0}^{\infty}\frac{x^n}{n!}=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots ex=n=0∑∞n!xn=1+1!x+2!x2+3!x3+4!x4+⋯- 正弦函数 sin x \sin x sinx 的麦克劳林级数:
sin x = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + ⋯ \sin x=\sum_{n = 0}^{\infty}\frac{(-1)^n x^{2n + 1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots sinx=n=0∑∞(2n+1)!(−1)nx2n+1=x−3!x3+5!x5−7!x7+⋯- 余弦函数 cos x \cos x cosx 的麦克劳林级数:
cos x = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ \cos x=\sum_{n = 0}^{\infty}\frac{(-1)^n x^{2n}}{(2n)!}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots cosx=n=0∑∞(2n)!(−1)nx2n=1−2!x2+4!x4−6!x6+⋯二、欧拉公式推导过程
欧拉公式 e i x = cos x + i sin x e^{ix}=\cos x + i\sin x eix=cosx+isinx 可通过麦克劳林级数严格推导,具体步骤如下:
建立 e i x e^{ix} eix 的展开式:
将 e x e^x ex 麦克劳林级数中的 x x x 替换为虚数 i x ix ix,得到
e i x = 1 + i x 1 ! + ( i x ) 2 2 ! + ( i x ) 3 3 ! + ( i x ) 4 4 ! + ( i x ) 5 5 ! + ( i x ) 6 6 ! + ⋯ e^{ix}=1+\frac{ix}{1!}+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+\frac{(ix)^5}{5!}+\frac{(ix)^6}{6!}+\cdots eix=1+1!ix+2!(ix)2+3!(ix)3+4!(ix)4+5!(ix)5+6!(ix)6+⋯利用虚数性质化简:
根据虚数单位的幂次性质 i 2 = − 1 i^2=-1 i2=−1, i 3 = − i i^3 = -i i3=−i, i 4 = 1 i^4 = 1 i4=1,
i 5 = i i^5 = i i5=i, i 6 = − 1 ⋯ i^6=-1\cdots i6=−1⋯ 对上述展开式进行化简:
e i x = 1 + i x 1 ! − x 2 2 ! − i x 3 3 ! + x 4 4 ! + i x 5 5 ! − x 6 6 ! + ⋯ e^{ix}=1+\frac{ix}{1!}-\frac{x^2}{2!}-\frac{ix^3}{3!}+\frac{x^4}{4!}+\frac{ix^5}{5!}-\frac{x^6}{6!}+\cdots eix=1+1!ix−2!x2−3!ix3+4!x4+5!ix5−6!x6+⋯分离实部与虚部:
将实部与虚部分别合并,可得
e i x = ( 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ ) + i ( x 1 ! − x 3 3 ! + x 5 5 ! − ⋯ ) e^{ix}=\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\right)+i\left(\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right) eix=(1−2!x2+4!x4−6!x6+⋯)+i(1!x−3!x3+5!x5−⋯)关联三角函数级数:
对比 cos x \cos x cosx 和 sin x \sin x sinx 的麦克劳林级数表达式,可知:
实部 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ = cos x 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots=\cos x 1−2!x2+4!x4−6!x6+⋯=cosx
虚部 x 1 ! − x 3 3 ! + x 5 5 ! − ⋯ = sin x \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots=\sin x 1!x−3!x3+5!x5−⋯=sinx
由此可得 欧拉公式:
e i x = cos x + i sin x e^{ix}=\cos x + i\sin x eix=cosx+isinx
欧拉公式通过幂级数展开,建立了指数函数与三角函数在复数域的深刻联系,在数学分析、复变函数及工程应用领域具有核心地位。
当 x x x 取特殊值 π π π 时,就化作了最美公式 —— 欧拉恒等式:
e i π = cos ( π ) + i sin ( π ) \large e^{i\pi} = \cos(\pi) + i\sin(\pi) eiπ=cos(π)+isin(π)
e i π = − 1 \large e^{i\pi} = -1 eiπ=−1
e i π + 1 = 0 \large e^{i\pi} + 1 = 0 eiπ+1=0
它融合了数学上最重要的 5 个常数,以极其简洁的方式,连接了不同的数学分支。
同时,也包含了物理学中的圆周运动、简谐振动、机械波、电磁波和概率波等,对后世产生了深远影响。

它仿佛一首完美而简洁的诗,道尽了数学之美。
难怪数学家们评价它为:“神创造的公式,我们只能看它却不能完全理解它”。
篇外:
泰勒级数不同领域的应用
泰勒级数展开在数学、物理学、工程学和计算机科学等领域有广泛的应用。
指数函数 e x e^x ex 可以用于计算复利、放射性衰变、自然生长和衰减过程。在物理学中,它描述量子力学中的波函数演化。
正弦函数 sin x \sin x sinx 和余弦函数 cos x \cos x cosx 都可以用于描述周期性现象,如声波、光波和电磁波。在工程学中,它们用于设计振荡器和滤波器。
自然对数 ln ( 1 + x ) \ln(1+x) ln(1+x) 可以用于计算连续复利。在物理学中,它描述某些类型的热力学过程。
几何级数 1 1 − x \frac{1}{1-x} 1−x1 和反向几何级数 1 1 + x \frac{1}{1+x} 1+x1 都可以用于计算无限级数的和,如在数列求和和概率论中的应用。
幂函数 ( 1 + x ) α (1+x)^{\alpha} (1+x)α 可以用于计算复利和金融数学中的增长模型。在物理学中,它描述某些类型的物理过程,如气体的压强-体积关系。
反正切函数 arctan x \arctan x arctanx 和反正弦函数 arcsin x \arcsin x arcsinx 都可以用于计算三角函数的反函数,解决涉及角度的问题。在电子学中,反正切函数用于设计积分器和微分器电路。
正切函数 tan x \tan x tanx 可以用于计算三角函数,描述角度和边长之间的关系。在物理学中,它描述周期性运动,如简谐振动。
泰勒级数展开形式使得它们在需要近似计算时非常有用,尤其是在数值分析和计算机科学中,可以简化复杂的数学表达式,进行数值计算和模拟。
常见泰勒公式展开
-
e x = ∑ n = 0 ∞ 1 n ! x n \large e^x = \sum_{n=0}^{\infty} \frac{1}{n!} x^n ex=∑n=0∞n!1xn, x ∈ ( − ∞ , + ∞ ) x \in (-\infty, +\infty) x∈(−∞,+∞)
-
sin x = ∑ n = 0 ∞ ( − 1 ) n ( 2 n + 1 ) ! x 2 n + 1 = x − 1 3 ! x 3 + 1 5 ! x 5 + ⋯ \large \sin x = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{2n+1} = x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 + \cdots sinx=∑n=0∞(2n+1)!(−1)nx2n+1=x−3!1x3+5!1x5+⋯, x ∈ ( − ∞ , + ∞ ) x \in (-\infty, +\infty) x∈(−∞,+∞)
-
cos x = ∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! x 2 n = 1 − 1 2 ! x 2 + 1 4 ! x 4 + ⋯ \large \cos x = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} x^{2n} = 1 - \frac{1}{2!} x^2 + \frac{1}{4!} x^4 + \cdots cosx=∑n=0∞(2n)!(−1)nx2n=1−2!1x2+4!1x4+⋯, x ∈ ( − ∞ , + ∞ ) x \in (-\infty, +\infty) x∈(−∞,+∞)
-
ln ( 1 + x ) = ∑ n = 0 ∞ ( − 1 ) n n + 1 x n + 1 = x − 1 2 x 2 + 1 3 x 3 + ⋯ \large \ln(1+x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{n+1} x^{n+1} = x - \frac{1}{2} x^2 + \frac{1}{3} x^3 + \cdots ln(1+x)=∑n=0∞n+1(−1)nxn+1=x−21x2+31x3+⋯, x ∈ ( − 1 , 1 ] x \in (-1, 1] x∈(−1,1]
-
1 1 − x = ∑ n = 0 ∞ x n = 1 + x + x 2 + x 3 + ⋯ \large \frac{1}{1-x} = \sum_{n=0}^{\infty} x^n = 1 + x + x^2 + x^3 + \cdots 1−x1=∑n=0∞xn=1+x+x2+x3+⋯, x ∈ ( − 1 , 1 ) x \in (-1, 1) x∈(−1,1)
-
1 1 + x = ∑ n = 0 ∞ ( − 1 ) n x n = 1 − x + x 2 − x 3 + ⋯ \large \frac{1}{1+x} = \sum_{n=0}^{\infty} (-1)^n x^n = 1 - x + x^2 - x^3 + \cdots 1+x1=∑n=0∞(−1)nxn=1−x+x2−x3+⋯, x ∈ ( − 1 , 1 ) x \in (-1, 1) x∈(−1,1)
-
( 1 + x ) α = 1 + ∑ n = 1 ∞ α ( α − 1 ) ⋯ ( α − n + 1 ) n ! x n \large (1+x)^{\alpha} = 1 + \sum_{n=1}^{\infty} \frac{\alpha(\alpha-1) \cdots (\alpha-n+1)}{n!} x^n (1+x)α=1+∑n=1∞n!α(α−1)⋯(α−n+1)xn, x ∈ ( − 1 , 1 ) x \in (-1, 1) x∈(−1,1)
-
arctan x = ∑ n = 0 ∞ ( − 1 ) n 2 n + 1 x 2 n + 1 = x − 1 3 x 3 + 1 5 x 5 + ⋯ + x \large \arctan x = \sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1} x^{2n+1} = x - \frac{1}{3} x^3 + \frac{1}{5} x^5 + \cdots + x arctanx=∑n=0∞2n+1(−1)nx2n+1=x−31x3+51x5+⋯+x, x ∈ [ − 1 , 1 ] x \in [-1, 1] x∈[−1,1]
-
arcsin x = ∑ n = 0 ∞ ( 2 n ) ! 4 n ( n ! ) 2 ( 2 n + 1 ) x 2 n + 1 = x + 1 6 x 3 + 3 40 x 5 + 5 112 x 7 + 35 1152 x 9 + ⋯ \large \arcsin x = \sum_{n=0}^{\infty} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} = x + \frac{1}{6} x^3 + \frac{3}{40} x^5 + \frac{5}{112} x^7 + \frac{35}{1152} x^9 + \cdots arcsinx=∑n=0∞4n(n!)2(2n+1)(2n)!x2n+1=x+61x3+403x5+1125x7+115235x9+⋯, x ∈ ( − 1 , 1 ) x \in (-1, 1) x∈(−1,1)
-
tan x = ∑ n = 1 ∞ B 2 n ( 2 n ) ! ( ( − 4 ) n ( 1 − 4 n ) ( 2 n − 1 ) ) x 2 n − 1 = x + 1 3 x 3 + 2 15 x 5 + 17 315 x 7 + 62 2835 x 9 + 1382 155925 x 11 + 21844 6081075 x 13 + 929569 638512875 x 15 + ⋯ \large \tan x = \sum_{n=1}^{\infty} \frac{B_{2n}}{(2n)!} \left(\frac{(-4)^n (1-4^n)}{(2n-1)} \right) x^{2n-1} = x + \frac{1}{3} x^3 + \frac{2}{15} x^5 + \frac{17}{315} x^7 + \frac{62}{2835} x^9 + \frac{1382}{155925} x^{11} + \frac{21844}{6081075} x^{13} + \frac{929569}{638512875} x^{15} + \cdots tanx=∑n=1∞(2n)!B2n((2n−1)(−4)n(1−4n))x2n−1=x+31x3+152x5+31517x7+283562x9+1559251382x11+608107521844x13+638512875929569x15+⋯, x ∈ ( − π 2 , π 2 ) x \in (-\frac{\pi}{2}, \frac{\pi}{2}) x∈(−2π,2π)
B n B_n Bn 表示伯努利数
via:
-
歐拉恆等式──最優美的數學定理 | 線代啟示錄
https://ccjou.wordpress.com/2012/05/11/歐拉恆等式-最優美的數學定理/ -
无穷级数求和 7 个公式_如何正确地理解欧拉公式 - 优快云 博客 weixin_39851048 于 2020-11-20 00:56:39 发布
https://blog.youkuaiyun.com/weixin_39851048/article/details/109915175 -
-
e , i , π e, i, \pi e,i,π 及弧度制的详细介绍及直观推导请分别参考:
-
自然底数 e e e:怎么就“自然”了? - 知乎
https://zhuanlan.zhihu.com/p/48391055 -
虚数 i i i: 虚数 i i i 真的很“虚”吗? - 知乎
https://zhuanlan.zhihu.com/p/48392273 -
π \pi π:古人是如何寻找到 π \pi π 的? - 知乎
https://zhuanlan.zhihu.com/p/48307582 -
弧度制:一圈为何是360°? - 知乎
https://zhuanlan.zhihu.com/p/48767522
-
-
傻子都能看懂的 —— 详解欧拉公式推导_欧拉公式推导全过程-优快云博客 越来越胖的 GuanRunwei 已于 2023-12-20 15:20:34 修改
https://blog.youkuaiyun.com/qq_38890412/article/details/117334679 -
“数学之王” 传奇:有数字的地方就有欧拉 原创 科学方程式 2024 年 06 月 19 日 17:11 北京
https://mp.weixin.qq.com/s/NUJ4zu5-V1NDGhKYIhzmVg -
史上最美数学公式 原创 蔡驰南 2024年06月05日 12:38 浙江
https://mp.weixin.qq.com/s/wG6_91ZShQGr-bvHy7zkxg
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








