混淆矩阵及建立在其基础上的评价指标

混淆矩阵

在机器学习中，混淆矩阵也称为误差矩阵，常用来可视化地评估分类模型的性能。在分类问题中，假设共有$K$个类别，混淆矩阵是一个$K$行$K$列的方阵，其每一行代表了样本的真实归属类别，每一行的数据之和表示属于该类别的真实样本总数；每一列代表了样本的预测类别，每一列的数据之和表示被预测为该类别的样本总数。

对于二分类问题，根据样本的真实类别与预测类别的组合，可能产生 4 种不同的结果：真正类（True Positive, TP）、假正类（False Positive, FP）、真负类（True Negative, TN）、假负类（False Negative, FN）。这里的 True 表示样本的预测类别与真实类别相同，即预测正确；False 表示样本的预测类别与真实类别不同，即预测错误；Positive 表示样本的类别标签为正，Negative 表示样本的类别标签为负。

• TP——预测正确（T），预测类别标签为正（P），即将正类正确预测为正类。
• FN——预测错误（F），预测类别标签为负（N），即将正类错误预测为负类。
• FP——预测错误（F），预测类别标签为正（P），即将负类错误预测为正类。
• TN——预测正确（T），预测类别标签为负（N），即将负类正确预测为负类。

令 TP、FP、TN、FN 分别表示其对应的样本数，则样本总数为 TP + FP + TN + FN，其中，预测正确的样本数量是 TP + TN，预测错误的样本数量是 FP + FN，分类结果得到的混淆矩阵如下表所示。
$$\text{TP}+\text{FP}+\text{TN}+\text{FN}=样本总数$$

表 二分类的混淆矩阵

真实类别 $\backslash$ 预测类别	正类 (Positive)	负类 (Negative)
正类 (Positive)	真正类 (TP)	假负类 (FN)
负类 (Negative)	假正类 (FP)	真负类 (TN)

例如，下图给出了一个三分类的混淆矩阵。第一行说明有 49 个真正属于类别 1 的样本被正确预测为类别 1，有 1 个真正属于类别 1 的样本被错误预测为类别 2。

在信息科学相关专业把positive、negative翻译成阳性、阴性的都是没脑子。这不是在做核酸检测。

评价指标

根据混淆矩阵，可以定义正确率和其他常用的评价分类模型性能的标准。

1. 正确率和错误率

正确率（Accuracy）是评价分类器性能的主要指标。对于给定的测试样本集，正确率定义为分类正确的样本数占总样本数的比例。

定义为分类器正确分类的样本数与参与分类的样本总数之比。即

$$\text{Accuracy}=\frac{1}{N}\sum _{i=1}^{N}I(f(x_i;\theta )=y_i)$$

式中，$N$为测试样本总数；$I(\cdot )$为指示函数（Indicative Function），即当$f(x_i;\theta )=y_i$时，$I(f(x_i;\theta )=y_i)=1$，否则，$I(f(x_i;\theta )=y_i)=0$。

对于二分类问题，正确率的计算公式为

$$\text{Accuracy}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{TN}+\text{FN}}$$

错误率（Error Rate）是与正确率相对应的性能指标，正确率越高，则错误率越低；反之，正确率越低，则错误率越高。对于给定的测试样本集，错误率定义为分类器错误分类的样本数与参与分类的样本总数之比。即

$$\text{ErrorRate}=\frac{1}{N}\sum _{i=1}^{N}I(f(x_i;\theta )\ne y_i)=1-\text{Accuracy}$$

对于二分类问题，错误率的计算公式为

$$\text{ErrorRate}=1-\text{Accuracy}=\frac{\text{FP}+\text{FN}}{\text{TP}+\text{FP}+\text{TN}+\text{FN}}$$

2. sensitivity（灵敏度）和specificity（特异性）

Sensitivity（灵敏度）：它衡量的是在所有实际为正类别的样本中，被正确识别为正类别（即预测正确的正样本）的比例。其计算公式为：

$$\text{Sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}}$$

灵敏度等于True Positive Rate（TPR，真正类率）或Recall（查全率）。

Specificity（特异性）：也称为True Negative Rate（TNR，真负类率）。它衡量的是在所有实际为负类的样本中，被正确识别为负类（即预测正确的负样本）的比例。其计算公式为：

$$\text{Specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}}$$

特异性称为True Negative Rate（TNR，真负类率）。

这两个指标帮助了解分类模型在不同类别上的表现情况。高sensitivity意味着模型能够很好地识别出正类别，很少有正例被误判为负例；而高specificity则意味着模型能很好地识别出负类，很少有负例被误判为正例。灵敏度和特异性是一对矛盾的指标。在实际应用中，提高灵敏度可能会导致特异性下降，反之亦然。这是因为：

• 如果一个检测方法过于敏感（即倾向于将更多的样本识别为正例），那么它可能会错误地将一些实际上为负例的样本识别为正例，从而降低特异性。
• 反之，如果一个检测方法过于特异（即倾向于将更多的样本识别为负例），那么它可能会错误地将一些实际上为正例的样本识别为负例，从而降低灵敏度。

因此，在设计和评估诊断测试或分类模型时，需要在这两者之间找到一个平衡点，以确保既能有效识别真正的正例，又能避免错误地将负例识别为正例。

2. ROC 曲线和ROC 曲线下的面积（AUC）

在众多的分类模型中，如逻辑斯谛回归模型、Softmax 回归模型等，为测试样本输出的是预测概率，然后将这个预测概率与预设的一个分类决策阈值（Threshold）进行比较，若预测概率大于阈值则认为样本的类别为正类，反之为负类。这使得模型多了一个超参数，并且这个超参数会影响模型的推广能力。然而，实际上，并不是只有上述这一种方法，还可以根据这个预测概率值，对测试样本进行排序，将“最可能”为正类的样本排在最前面，“最不可能”为正类的样本排在最后面。然后，规定分类操作就是在这个样本序列中以某个截断点（Cut Point）为基准将样本序列划分为两部分，排在前面的那一部分当作正类，排在后面的那一部分当作负类。这样，就可以根据不同的任务需求采用不同的截断点，假如更加强调查准率，则可将截断点移到靠前的位置（即减小 FP）；若更加强调查全率，则可将截断点移到靠后的位置（即减小 FN）。因此，排序本身的性能好坏，体现了综合考虑分类模型在不同任务下的期望推广性能的好坏。受试者工作特征（Receiver Operating Characteristic，ROC）曲线就是从这个角度出发来研究分类模型推广性能的工具。

受试者工作特征（ROC）的概念源于信号探测理论。ROC 曲线与 P-R 曲线类似，可以直观地表示分类模型的性能，两者的区别之处在于 ROC 曲线描述了 FPR - TPR 的关系，而 P-R 曲线描述了 Precision - Recall 的关系。首先根据分类模型的预测结果对样本进行排序；然后从前往后逐个将样本作为正类进行预测，每当预测一个样本，就对已预测的所有样本计算“真正类率”（True Positive Rate, TPR）和“假正类率”（False Positive Rate, FPR）两个重要的值；最后，以 TPR 为纵轴、FPR 为横轴在二维平面上作图，就得到了 ROC 曲线。

TPR 和 FPR 的定义分别为

$$\text{TPR}=\mathrm{Sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}}$$

$$\text{FPR}=1-\mathrm{Specificity}=\frac{\text{FP}}{\text{FP}+\text{TN}}$$

TPR 表示在真实类别为正类的所有样本（TP + FN）中被正确预测为正类的样本（TP）所占的比例，其值等于查全率；FPR 表示在真实类别为负类的所有样本（TN + FP）中被错误预测为正类的样本（FP）所占的比例。

ROC 曲线的横坐标和纵坐标都在 [0,1] 之间，显然 ROC 曲线下面积 AUC 值不大于 1。ROC 曲线具有以下性质：

• (0,0) 点：假正类率 FPR 和真正类率 TPR 都为 0，即分类模型将全部样本都预测为负类样本。
• (0,1) 点：假正类率 FPR 为 0，真正类率 TPR 为 1，即分类模型将全部样本都预测正确，这是“理想模型”。
• (1,0) 点：假正类率 FPR 为 1，真正类率 TPR 为 0，即分类模型将全部样本都预测错误。
• (1,1) 点：假正类率 FPR 和真正类率 TPR 为 1，即分类模型将全部样本都预测为正类样本。
• TPR = FPR 的对角线：分类模型将样本预测为正类样本的结果有一半是正确的，有一半是错误的，表示的是“随机猜测”模型的预测效果。($\mathrm{Sensitivity}=0.5,\mathrm{Specificity}=0.5$)

于是，可以得到基本的结论：若 ROC 曲线在对角线以下，则表示该分类模型的预测效果比“随机猜测”还差；反之，若 ROC 曲线在对角线以上，则表示该分类模型的预测效果比“随机猜测”要好。当然，希望 ROC 曲线尽量位于对角线以上，也就是向左上角（0,1）点凸。

现实中通常利用有限个测试样本来绘制 ROC 曲线，只能获得有限个（FPR, TPR）坐标对，无法绘制光滑的 ROC 曲线。

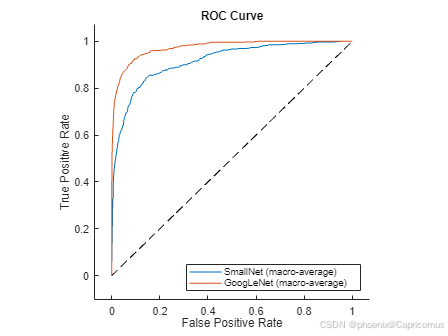
在进行分类模型比较时，若一个分类模型的 ROC 曲线被另一个分类模型的 ROC 曲线完全覆盖，则可以断言后者的性能优于前者；如果两个分类模型的 ROC 曲线发生交叉，则比较难断面这两个分类模型孰优孰劣。为了将 ROC 曲线概括成单一的度量值，通常考虑使用 ROC 曲线下的面积（AUC）作为度量指标。

AUC 的值表示 ROC 曲线下的面积，取值不会大于 1。又由于 ROC 曲线一般都处于 TPR = FPR 这条对角线的上方，所以 AUC 的取值范围一般在 [0.5,1] 之间。使用 AUC 值作为评价指标的原因在于大多数情况下 ROC 曲线并不能清晰地评价哪个分类模型的性能更好，而 AUC 量化了 ROC 曲线的分类能力，AUC 值越大的分类模型，其推广性能越好。

MATLAB

MATLAB在统计学和机器学习工具包中提供了两种画混淆矩阵的函数。