【机器学习】决策树(二)----CART算法

才写完上一篇，就和朋友讨论到了集成学习的厉害，随即就扯到了CART，本来一直不明白CART回归树明明输出的一块一块的区域，为什么还叫回归。。被朋友一图点醒，果然还是要边学理论边实践，才会有更好的理解。

CART算法同样由特征选择、树的生成以及树的剪枝组成。
总的来说就两步：一、基于训练集生成决策树，生成的决策树要尽量大；二、用验证集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

【CART生成】

决策树类型	生成准则
回归树	平方误差最小化(即最小二乘法)
分类树	基尼指数最小化

回归树的生成

假设$X$和$Y$分别为输入变量和输出变量，并且$Y$是连续变量，给定训练数据集$D={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$，我们生成回归树，生成算法的思想就是将输入空间(即特征空间)划分为$M$个单元$R_1,R_2,...,R_M$，每一个单元有一个固定的输出值$c_m$。
下面我们来一步一步的分析这个算法的过程，它的主要思路就是，我们对一个空间遍历所有划分点，求出令两个空间真实输出值与最优输出值平方误差之和最小的那个划分点。然后对划分出的两个空间继续划分，用同样的方式找到最优划分点，重复直至终止条件

生成回归树(最小二乘回归树算法)：

输入：训练数据集$D$
输出：回归树$f(x)$

①先将输入变量排序；

②选择第$j$个变量$x_j$和它的取值$s$作为切分变量和切分点，并定义两个区域：$R_1(j,s)=\{x|x_j\le s\}$和$R_2(j,s)=\{x|x_j> s\}$

③利用平方误差最小准则求这两个区域上的最优输出值$c_1$和$c_2$。对于一个区域$R_m$来说，它的最优输出值$\hat c_m$就是$R_m$上的所有实例$x_i$对应的输出$y_i$的均值；

$\color{blue}{这里针对的是这个切分上两个区域的最优值，最后我们要比较所有切分得}$
$\color{blue}{到的最优值来确定切分点}$
$\color{red}{为什么最优输出值\hat c_m就是R_m上的所有实例x_i对应的输出y_i的均值？用公式证明：}$

$\color{red}{\min\limits_{c_m}\sum\limits_{x_i\in R_m}(y_i-c_m)^2即为：}$

$\color{red}{\frac{\partial\sum\limits_{x_i\in R_m}(y_i-c_m)^2}{\partial c_m}=\sum\limits_{x_i\in R_m}(2c_m-2y_i)=0}$

$\color{red}{\sum\limits_{x_i\in R_m}c_m=\sum\limits_{x_i\in R_m}y_i}$
$\color{red}{假设有N_m个变量在区域R_m中，则上式写为：}$
$\color{red}{N_m\times c_m=\sum\limits_{x_i\in R_m}y_i}$
$\color{red}{c_m=\frac{1}{N_m}\sum\limits_{x_i\in R_m}y_i=\bar y_i}$

④遍历变量$j$，求解$\min\limits_{j,s}[\min\limits_{c_1}\sum\limits_{x_i\in R_1(j,s)}(y_i-c_1)^2+\min\limits_{c_2}\sum\limits_{x_i\in R_2(j,s)}(y_i-c_2)^2]$，即找到最优切分变量$j$和切分点$s$；

⑤根据找到的最优切分变量和切分点(j,s)划分区域$R_1$和$R_2$，并得到这两个区域对应的输出值$\hat c_1$和$\hat c_2$；

$R_1(j,s)=\{x|x_j\le s\}$和$R_2(j,s)=\{x|x_j> s\}$
$\hat c_m=\frac{1}{N_m}\sum\limits_{x_i\in R_m(j,s)}y_i$，$x\in R_m$，$m=1,2$

⑥继续对这两个子区域调用步骤②~⑤，直至满足停止条件；

⑦将输入空间划分为$M$个区域$R_1,R_2,...,R_M$，生成决策树：

$f(x)=\sum\limits_{m=1}^M\hat c_mI(x\in R_m)$

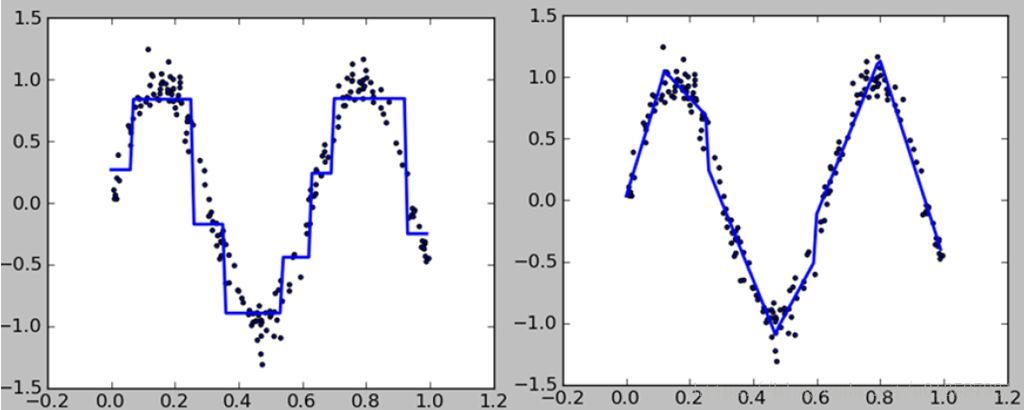
左图蓝线是一棵回归树的拟合，很明显，横平竖直，一条横线就代表了一个区域的输出值。右图是用了集成学习后的多棵回归树。

分类树的生成

分类树用基尼指数选择最优特征，同时决定该特征的最优二值切分点。
回顾一下基尼指数，

基尼指数

输入：训练数据集$D$、特征$A$
输出：特征A对训练数据集D的基尼指数$Gini(D,A)$
$\color{blue}{1.若样本点属于第一个类的概率是p，则概率分布的基尼指数为}$
　　　$Gini(p)=2p(1-p)$
　　　$\color{red}{此处是二分类情况，CART算法中会将特征的多个取值变为one-vs-rest的形式(借用LR和SVM做多分类的一种方法来比喻)变成二分类，来计算某特征所有取值的Gini指数}$
$\color{blue}{2.特征A对数据集D的基尼指数Gini(D,A)}$
　　　$Gini(D,A)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$

生成分类树(基尼指数)：

输入：训练数据集$D$，停止计算的条件；
输出：CART决策树
根据训练数据集，从根节点开始，递归地对每个节点进行以下操作，构建二叉决策树：

①设节点的训练数据集为$D$，计算所有特征和其所有可能切分点对该数据集的基尼指数；

假设该节点训练数据集$D$上有n个特征$A_i\in\{A_1,A_2,...,A_n\}$，对每一个特征而言，又有不同的取值$a_j\in{a_1,a_2,...a_m}$(即切分点)，$m$根据不同特征的可取值数目而定。我们要计算每一个特征的每一种取值的基尼指数。(根据样本点对$A_i=a_j$的测试为“是”或“否”，将数据集分割为两个部分，然后代入公式求解基尼指数)

②在所有可能的特征$A_i$和其所有可能的切分点$a_j$中选择基尼指数最小的特征，及其对应的切分点作为最优特征与最优切分点。根据最优特征与最优切分点，从现节点生成两个子节点，将训练数据集根据特征分配到两个子节点中；

③对这两个子节点递归调用①，②，直至满足停止条件；

④生成CART决策树

$\color{red}{一般算法停止条件为节点中样本个数小于预定阈值，或样本集的基尼指数小于预定}$
$\color{red}{阈值(样本基本属于同一类)，或没有更多特征了。}$

观察两个算法发现，CART生成算法生成的树都是二叉树

【CART剪枝】

CART剪枝和前面的剪枝算法比起来稍微有些难懂，主要在于有很多模糊的地方，尤其是《统计学习方法》中对$g(t)=\frac{C(t)-C(T_t)}{|T_t|-1}$的描述是表示剪枝后整体损失函数减少的程度，让我不能理解为什么要在$T_0$中剪去$g(t)$最小的$T_t$。后来总算理清楚了。
下面让我来理一理这个算法到底是一个什么样的思路。

一、首先什么情况下我们会选择剪枝。

和上一篇剪枝算法一样，我们都需要用到决策树的损失函数这一概念。
　　　　　　　　$C_α(T)=C(T)+α|T|$
我们用$C_α(T)$表示子树$T$的整体损失函数，$C(T)$表示训练数据的预测误差(有多种计算手段，如基尼指数，信息熵，这里用基尼指数应该会更好，因为CART决策树就是根据基尼指数一层一层往下生成的)，$|T|$指的是子树$T$的叶节点个数，可以说是表现了子树$T$的复杂度，而参数$α$则是用来权衡训练数据的拟合程度和模型复杂程度。我们希望剪枝后的损失函数要小于剪枝前的损失函数，这样剪枝才有意义嘛。因此当剪枝后的损失函数要小于剪枝前的损失函数，我们会选择剪枝。
虽然这些在前篇已经阐述了一遍，但这个对理解剪枝算法尤为重要。

二、参数$α$在CART剪枝算法中的重要意义

在前面的剪枝算法中，我们可以发现，算法的输入中是有$α$的，也就是说$α$是一个给定的值。
我们可以看一下，$α$值的变化会造成什么样的影响。当$α$偏大，我们希望损失函数越小越好，因此最优子树$|T_α|$会偏小，极端情况是$α\to\infty$时，根节点组成的单节点树是最优的；当$α$偏小，同理，最优子树|T_α|会偏大，极端情况下是$α=0$时，整体树就是最优的。
具体到CART算法中，我们对每一个内部节点$t$计算它作为单节点树的损失函数$C_α(t)$，和它作为根节点子树(子树$T_t$)的损失函数$C_α(T_t)$。
$C_α(t)=C(t)+α$　　$\color{red}{因为单节点树可以看做只是一个叶子节点，所以|t|为1}$
$C_α(T_t)=C(T_t)+α|T_t|$
下面就是关键所在了，我们是否需要剪枝，要看这个内部节点作为单节点树的损失函数和它作为根节点子树的损失函数的大小关系。
1.若是作为单节点树的损失函数要更小一些，那我当然是把这个内部节点变为叶子节点更好咯，所以要进行剪枝；
2.若是作为根节点子树的损失函数要更小一些，那么保留它继续做一个根节点子树的形态更好，也就是不剪枝。
3.若是两个的损失函数相等，那么根据模型越简单越好的原则，我们希望节点少一点咯，而单节点树明显节点更少，因此选择剪枝。

换成数学语言来说：

当$C_α(t)>C_α(T_t)$时，不剪枝；
当$C_α(t)\le C_α(T_t)$时，剪枝。
$\color{red}{可得：C(t)+α\le C(T_t)+α|T_t|}$　　$\color{red}{α\ge\frac{C(t)-C(T_t)}{|T_t|-1}}$
也就是说，当$α\ge\frac{C(t)-C(T_t)}{|T_t|-1}$时我们可以对$T_t$进行剪枝。

三、CART剪枝算法思想

我们将整体树记作$T_0$，对$T_0$中每一内部节点$t$计算$g(t)=\frac{C(t)-C(T_t)}{|T_t|-1}$，这里《统计学习方法》给出了一个解释，即$g(t)$表示了剪枝后整体损失函数减少的程度。这句话是没有问题的，主要在于为什么要将$α$设置为最小的$g(t)$。原因如下：

假设有$5$个内部节点$t_1,t_2,t_3,t_4,t_5$，我们分别求了它们的$g(t)$，并得到这样的大小关系$g(t_1)< g(t_2)< g(t_3)< g(t_4)< g(t_5)$，那么当我把$α_1$设置为$g(t_1)$时，只有内部节点$t_1$符合剪枝要求，而其他的内部节点并不用剪枝，因此由$t_1$剪枝后得到的子树$T_1$就是$[α_1,α_2)$的最优子树了。($α_2$取开区间的原因就是若是闭区间，对于$α_2$来说节点$t_1$和$t_2$都可以做剪枝啦，我就不知道谁是最优子树啦)

我们通过第一次剪枝得到了子树$T_1$，我们继续对这个子树进行以上步骤，求出每一个内部节点的$g(t)$，找到最小的赋值给$α_2$，在划分出子树$T_2$，就这样递归下去，直到$T_k$是一棵由根节点及两个叶子节点构成的树为止。

最后，我们利用独立的验证数据集，对子树序列$T_0,T_1,...T_n$中各棵子树测试其平方误差或基尼指数。平方误差或基尼指数最小的决策树被认为是最优的决策树。而且每个子树$T_0,T_1,...T_n$都对应着一个参数$α_0,α_1,...α_n$，因此当最优子树$T_k$确定时，对应的$α_k$也确定了，即得到最优决策树$T_α$。

CART剪枝算法

输入：CART算法生成的决策树$T_0$；
输出：最优决策树$T_α$

①设$k=0,T=T_0$；

②设$α=+\infty$；

③自下而上地对各内部节点$t$计算$C(T_t),|T_t|$以及

　　　　　　　　$g(t)=\frac{C(t)-C(T_t)}{|T_t|-1}$
　　　　　　　　$α=min(α,g(t))$

④对$g(t)=α$的内部节点$t$进行剪枝，并对叶节点$t$以多数表决法决定其类，得到树$T$ ；

$\color{blue}{多数表决法在后面集成学习中会提到}$

⑤设$k=k+1,α_k=α,T_k=T$；

⑥如果$T_k$不是由根节点及两个叶节点构成的树，则返回步骤②；否则令$T_k=T_n$；

$\color{red}{注意这里是返回第二步②，不是返回第三步也不是第四步，若是回到第三步，则α会一直}$
$\color{red}{是第一个最小的g(t)，即α_1}$
我买的这本李航老师的《统计学习方法》上是未勘误的版本，老师给出了勘误表，大家可以看一下
http://blog.sina.com.cn/s/blog_7ad48fee01017dpi.html
⑦采用交叉验证法在子树序列$T_0,T_1,...T_n$中选取最优子树$T_α$。

【感想】

对于算法，一定要静下心来慢慢推一遍，少一块拼图，可能就会影响后面的理解。就像CART算法一样，中间有很多疑惑的地方，如果不去弄清楚，则逻辑就会变得不通。至此，机器学习算法中的算法已经复习了五个，后面可以开始集成学习的复习了。此后会多加实践内容，光看理论总是有些空，而且我代码能力也太弱鸡了，必须训练T T