CF 259

C. Little Pony and Expected Maximum

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Twilight Sparkle was playing Ludo with her friends Rainbow Dash, Apple Jack and Flutter Shy. But she kept losing. Having returned to the castle, Twilight Sparkle became interested in the dice that were used in the game.

The dice has m faces: the first face of the dice contains a dot, the second one contains two dots, and so on, the m-th face contains mdots. Twilight Sparkle is sure that when the dice is tossed, each face appears with probability . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.

Input

A single line contains two integers m and n (1 ≤ m, n ≤ 105).

Output

Output a single real number corresponding to the expected maximum. The answer will be considered correct if its relative or absolute error doesn't exceed 10  - 4.

Sample test(s)

input

6 1

output

3.500000000000

input

6 3

output

4.958333333333

input

2 2

output

1.750000000000

Note

Consider the third test example. If you've made two tosses:

1. You can get 1 in the first toss, and 2 in the second. Maximum equals to 2.
2. You can get 1 in the first toss, and 1 in the second. Maximum equals to 1.
3. You can get 2 in the first toss, and 1 in the second. Maximum equals to 2.
4. You can get 2 in the first toss, and 2 in the second. Maximum equals to 2.

The probability of each outcome is 0.25, that is expectation equals to:

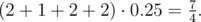
You can read about expectation using the following link: http://en.wikipedia.org/wiki/Expected_value

发现是一道好简单的概率。。。

一个筛子有m个面，第i个面上有i个点，现在投掷n次，问所得到的最大点数的期望。

每次有m种情况，共投掷n次，那么共有m*n种情况。

其中最大点数是1的有1种，最大点数是2的有(2^n-1)种，最大点数是3的有(3^n-2^n)种...最大点数是m的有(m^n-(m-1)^n)种。

那么期望可表示为 。

化简以后便是 m - ( (1/m)^n + (2/m)^n + ...+ ((m-1)/m)^n )。

#include <stdio.h>
#include <iostream>
#include <map>
#include <set>
#include <stack>
#include <vector>
#include <math.h>
#include <string.h>
#include <queue>
#include <string>
#include <stdlib.h>
#include <algorithm>
#define LL long long
#define _LL __int64
#define eps 1e-12
#define PI acos(-1.0)
#define C 240
#define S 20
using namespace std;


double mod_exp(double a, int n)
{
	double ret = 1;

	while(n)
	{
		if(n&1)
			ret = ret * a;
		a = a*a;
		n >>= 1;
	}
	return ret;
}

int main()
{
	int n,m;

	while(~scanf("%d %d",&m,&n))
	{
		double ans = 0;

		for(int i = 1; i <= m-1; i++)
		{
			ans += mod_exp( (i*1.0)/(m*1.0), n);
		}

		ans = m-ans;
		printf("%.12lf\n",ans);
	}
	return 0;
}