该文提出了一种结合曲线自适应和模拟退火的蝗虫优化算法(SA-CAGOA)，旨在解决基础蝗虫算法的局部最优问题和收敛速度。通过引入余弦和圆弧自适应策略改进参数更新，增强全局搜索能力。同时，利用模拟退火的Metropolis准则，允许接受较差解以跳出局部极值。算法在迭代过程中动态调整搜索范围，提高优化性能。实验结果展示了SA-CAGOA的有效性。
基于曲线自适应和模拟退火的蝗虫优化算法
文章目录
摘要：针对蝗虫优化算法容易陷入局部极值点、收敛速度慢、精度较差等缺点，提出曲线自适应和模拟退火蝗虫优化算法。首先，引入曲线自适应代替蝗虫优化算法关键参数的线性自适应，提高了算法的全局搜索能力;其次，在此基础上引入模拟退火算法，对蝗虫算法的劣势解具有一定概率的接收，使算法具有跳出局部最优，实现全局最优的能力。自适应缩小模拟退火中蝗虫位置随机解的范围，有利于进一步提高蝗虫算法的开发能力。
1.蝗虫优化算法
基础蝗虫优化算法的具体原理参考，我的博客：https://blog.youkuaiyun.com/u011835903/article/details/107694862
2. 基于曲线自适应和模拟退火的蝗虫优化算法(SA-CAGOA)
2.1 基于曲线自适应的蝗虫优化算法(CAGOA)
本文提出的 CAGOA 中主要采用两种曲线自适应策略，即余弦自适应(式(4))和圆弧自适应(式(5))。式(4)和(5)分别替代蝗虫优化算法中的线性自适应更新参数 c 的方法，从而形成两种新的 CAGOA，分别简称为 CAGOA1 和 CAGOA2。参数 c 影响着蝗虫的搜索范围，参数由大到小对应蝗虫算法由全局搜索到局部搜索的转变。曲线自适应和线性自适应的不同之处在于参数 c 的下降趋势，线性自适应以相同速率减小，而余弦自适应调整策略在开始和结束时下降速率会很小，下降缓慢，有助于增强蝗虫在开始时的全局搜索和后期的局部搜索能力。除此之外，余弦自适应参数 c 的值在前期比线性自适应的值大，可以加大蝗虫的搜索范围，增强蝗虫勘探能力;后期参数的值比线性自适应小，可以减小蝗虫的搜索范围，增强蝗虫探索能力。
c
=
{
c
o
s
(
π
×
l
/
m
a
x
_
i
t
e
r
+
c
m
a
x
)
×
(
c
m
a
x
+
c
m
i
n
)
/
2
(
c
m
a
x
−
l
)
/
m
a
x
_
i
t
e
r
)
2
(4,5)
c=\left\{\begin{array}{l} cos(\pi \times l/max\_iter+c_{max})\times(c_{max}+c_{min})/2 \\ (c_{max}-l)/max\_iter)^2 \end{array}\right. \tag{4,5}
c={cos(π×l/max_iter+cmax)×(cmax+cmin)/2(cmax−l)/max_iter)2(4,5)
2.2 Metropolis 准则
模拟退火算法采用 Metropolis 接收准则 ，以一定概率接收较差的解，使算法能够跳出局部最优，避免陷入局部搜索。假设物体在状态
i
i
i下的内能为
E
(
i
)
E(i)
E(i)，状态
j
j
j下的内能为
E
(
j
)
E(j)
E(j)。物体在某一温度
T
T
T下从状态
i
i
i 转移到状态
j
j
j，如果内能
E
(
j
)
＜
E
(
i
)
E(j) ＜ E(i)
E(j)＜E(i)，则接收
j
j
j 为当前状态;否则，若概率
P
i
，
j
T
P^T_{i，j}
Pi，jT 大于［0，1)的随机数，则仍接收状态
j
j
j 为当前状态，若概率
P
i
，
j
T
P^T_{i，j}
Pi，jT小于［0，1)的随机数，则保留状态
i
i
i为当前状态。
P
i
，
j
T
P^T_{i，j}
Pi，jT定义 如下:
P
i
j
T
=
{
1
E
(
j
)
⩽
E
(
i
)
e
(
−
E
(
j
)
−
E
(
i
)
K
T
)
others
(6)
P_{i j}^{T}=\left\{\begin{array}{ll} 1 & E(j) \leqslant E(i) \\ e^{\left(-\frac{E(j)-E(i)}{K T}\right)} & \text { others } \end{array}\right. \tag{6}
PijT={1e(−KTE(j)−E(i))E(j)⩽E(i) others (6)
其中:
E
(
i
)
E(i)
E(i)和
E
(
j
)
E(j)
E(j)分别表示固体在状态
i
i
i和
j
j
j下的内能;
K
K
K 为波尔兹曼常数。
2.3 模拟退火蝗虫随机位置
模拟退火在搜索过程引入了随机因素，在模拟退火中蝗虫的随机位置公式如下:
x
i
+
1
=
1
2
(
x
i
−
u
b
−
l
b
l
2
+
(
u
b
−
l
b
)
×
2
l
2
×
rand
)
(7)
x_{i+1}=\frac{1}{2}\left(x_{i}-\frac{u b-l b}{l^{2}}+\frac{(u b-l b) \times 2}{l^{2}} \times \text { rand }\right) \tag{7}
xi+1=21(xi−l2ub−lb+l2(ub−lb)×2× rand )(7)
其中:
x
i
x_i
xi 是蝗虫当前位置解;
x
i
+
1
x_{i+1}
xi+1 为蝗虫随机的下个位置解;
L
L
L是蝗虫的迭代次数;
u
b
、
l
b
ub、lb
ub、lb 分别为蝗虫位置的上界和下界;
r
a
n
d
rand
rand是 0 到 1 的随机数。式(7)中蝗虫随机位置范围随蝗虫迭代次数的增加而减小，这有利于提高蝗虫后期的开发能力。
2.4 SA-CAGOA 的实现步骤
a)随机生成个 N 蝗虫的初始化种群、初始化种群位置
X
i
X_i
Xi 、参数
c
m
a
x
、
c
m
i
n
c_{max} 、c_{min}
cmax、cmin 和最大迭代次数
m
a
x
i
t
e
r
a
t
i
o
n
max_{iteration}
maxiteration;
b)计算种群每个个体的适应度值，并保存适应度值最好个体的值到变量 fitness;
c)用式(4)或(5)更新参数
c
c
c;
d)用式(3)更新蝗虫的位置并计算每个蝗虫的适应度值;
e)设置初始温度
T
0
T_0
T0 ，结束温度
T
T
T，退火系数
r
r
r;
f)在得到蝗虫解的邻域内用式(7)随机选择新解，计算两
个解的适应度值，并根据 Metropolis 准则更新解;
g)若步骤 f)中得到的蝗虫适应度有更好的值，则更新变量 fitness;
h)判断算法是否达到终止条件，若达到，则终止循环返回结果 fitness，否则转到步骤 c)。
在上述的实现步骤 c)中，当使用式(4)更新参数 c，即采用余弦自适应策略时，形成的最终优化算法这里简称为 SA-CA-GOA1;而当使用式(5)更新参数 c，即采用圆弧自适应策略时，则形成的最终优化算法这里简称为 SA-CAGOA2。
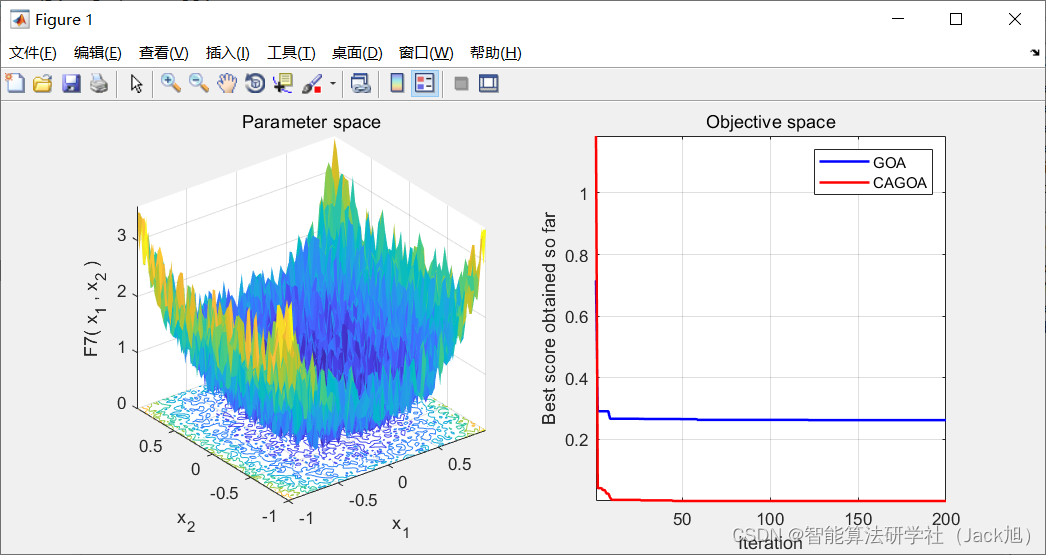
3.实验结果
4.参考文献
[1]李洋州,顾磊.基于曲线自适应和模拟退火的蝗虫优化算法[J].计算机应用研究,2019,36(12):3637-3643.
扫一扫
116
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
