【剪枝】——BIT-PRUNING一种稀疏的无乘法点积方法

论文：https://openreview.net/pdf?id=YUDiZcZTI8

摘要

点积是神经网络中的一个核心构建模块。然而，点积中的乘法（mult）消耗了大量的能量和空间成本，这对于在资源受限的边缘设备上部署提出了挑战。在这项研究中，我们通过利用无乘法、稀疏的点积来实现节能的神经网络。我们首先将整数权重和激活之间的点积重新公式化为由加法后跟位移（add-shift-add）组成的等效操作。在这种公式化中，加法操作的数量等于二进制格式中整数权重的位数。利用这一观察结果，我们提出了位剪枝（Bit-Pruning），它在训练期间移除每个权重值中不必要的位，以减少add-shift-add的能量消耗。 位剪枝可以看作是软重量剪枝，因为它剪掉了位而不是整个权重元素。在广泛的实验中，我们证明了使用位剪枝训练的稀疏无乘法网络比使用重量剪枝训练的稀疏乘法网络具有更好的准确性-能量折衷

简介

我们首先将整数权重和激活之间的点积(mult-add)重新公式化为由加法后跟位移和加法(add-shift-add)组成的等效操作。在这种公式化中，第一个加法操作的数量等于二进制格式中权重元素的位数。根据这一观察结果，我们提出了位剪枝(Bit-Pruning)，它在训练期间以数据驱动的方式移除不必要的add(因此移除权重中不必要的位)，以减少add-shift-add操作中的能量消耗。由于在二进制格式中优化困难，我们在具有位稀疏正则化(促进权重在二进制格式中稀疏)的高精度可微分mult-add网络上优化参数。训练后，获得的位稀疏mult-add网络被转换为由稀疏add组成的等效add-shift-add网络，以便在支持非结构化稀疏性的DNN加速器上进行高效推理。原理图

3 位剪枝

原始的卷积中的weight用2的幂次方表示，可以转换为：

这是通过使用加法沿着二进制向量Bj,m累积输入X·,u，然后使用移位乘以2m，最后通过加法聚合所有M位的结果来计算的

add-shift-add网络的二进制张量B被训练为具有权重W（图2）的高精度mult-add网络，并通过对权重W施加位稀疏正则化Lbit来实现B的稀疏化：

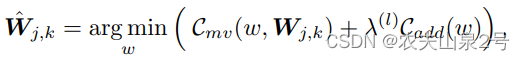
4 实验

在CIFAR-10和CIFAR-100上训练的ResNet18的准确性/能量折衷，用于不同的激活量化级别。比较了位剪枝（add-shift-add）（BP）和重量剪枝（mult-add）（WP）。位剪枝始终使用8位宽的二进制张量B，而重量剪枝使用与激活相同的量化级别来量化权重。提供了add-shift-add表示中的Weight-Pruning（WP(add)）和mult-add表示中的Bit-Pruning（BP(mult)）的结果。原始密集mult-add网络的乘加累积（MAC）约为0.55×106，根据表1，4位、8位和32位网络的估计能量消耗分别为26µJ、107µJ和1721µJ。

imagenet

请注意，位剪枝网络在mult-add表示中并未显示效率（BP(mult)），而重量剪枝网络在add-shift-add表示中也未显示效率（WP(add)）。这是因为位剪枝网络更喜欢二进制格式中稀疏的权重（图6d），这不一定是零，相反，重量剪枝网络更喜欢小权重，这不一定是二进制格式中稀疏的（图6c）