函数极限

在极限中，张宇老师引入了超实数的概念

一、定义

二、三大性质

1. 唯一性

如果$\underset{x\to x_0}{\lim }f(x)$，那么极限唯一。

2. 局部有界性

3. 局部保号性

三、无穷小

$\underset{x\to x_0}{\lim }f(x)=0$

1. 无穷小的性质

• 有限个无穷小的和是无穷小
• 有界函数与无穷小的乘积是无穷小
• 有限个无穷小的乘积是无穷小

2. 无穷小的比阶

3.常用的等价无穷小

四、无穷大

只要知道定义即可

五、计算

（一）方法

1. 极限四则运算法则

非常非常重要的结论

• $\lim \frac{f(x)}{g(x)}=A$，且 $\lim g(x)=0$，则$\lim f(x)=0$
• $\lim \frac{f(x)}{g(x)}=A\ne 0$，且 $\lim f(x)=0$，则$\lim g(x)=0$

2. 洛必达

2.1. 定义

2.2. 由洛必达得出两个重要的等价替换

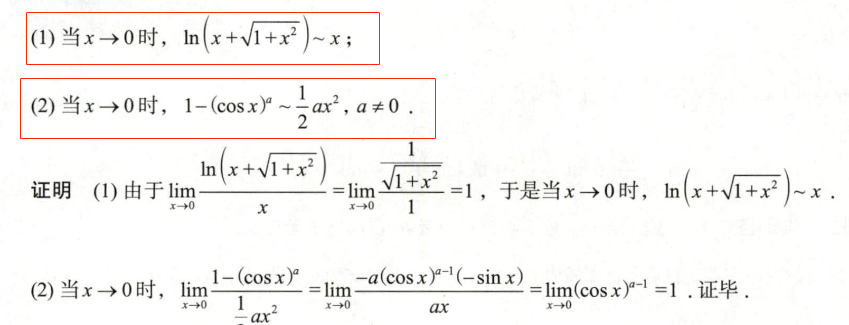
2.3. 洛必达判断大小关系

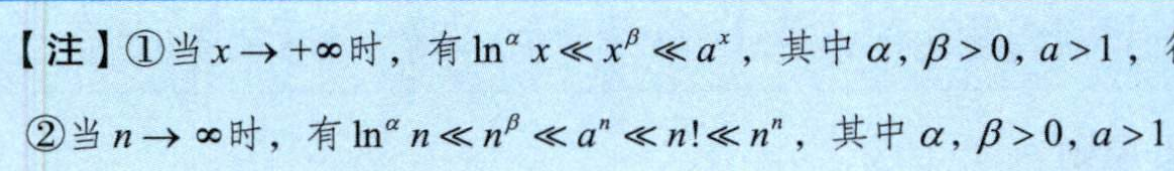
3. 泰勒公式

3.1. 公式

泰勒补充：

3.2. 展开原则

4. 夹逼准则

（二）七种未定式的计算

六、函数的连续与间断

本质上是极限的计算

1. 连续点的定义

设函数f(x)在点x₀的某一邻域内有定义，且有$\underset{x\to x_0}{\lim }f(x)=f(x_0)$，则称f(x)在点x₀处连续。

2. 间断点的定义与分类

以下设函数f(x)在点x₀的某去心邻域内有定义 要考虑双侧， 这是讨论间断点的前提，就比如在开区间（a，b）讨论a点的是否间断，没有意义

2.1. 可去间断点（第一类间断点）

若$\underset{x\to x_0}{\lim }f(x)=A\ne f(x_0)$(甚至在该点可以无定义，如 $\frac{1}{x}$)，则 x = x₀ 称为可去间断点 .

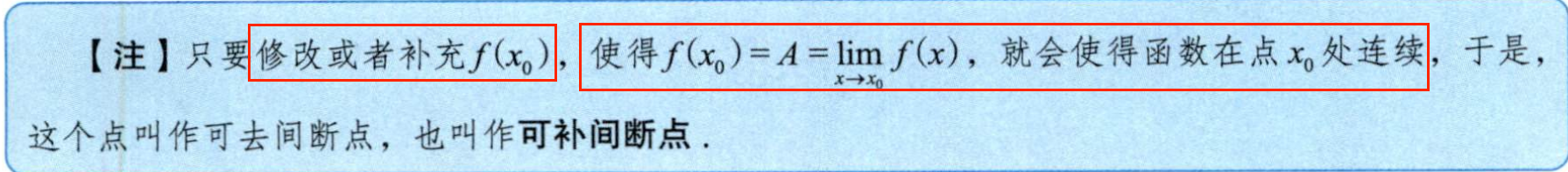
2.2. 跳跃间断点（第一类间断点）

2.3. 无穷间断点（第二类间断点）

2.4. 振荡间断点 （第二类间断点）

$\underset{x\to x_0}{\lim }f(x)振荡不存在，则称x=x_0为振荡间断点$。