尝试用double FFT的方法对变速箱的转速进行识别

本文链接：https://blog.youkuaiyun.com/twicave/article/details/148996968

这种信号分析模式我忘记出处了，应该还能找到，回头增补上来。原理很简单，因为频谱中的转速体现为边频带，所以，这种方法是在析取边频带的拼点。因为FFT对周期性信号非常敏感。边频带虽然对变速箱信号会发生混叠，无法清晰识别，但是对FFT而言可以轻松析取。

注意析取时，至少需要排除：0Hz和原始采样信号的周期那个频点，这两个频点要丢弃掉。

0.两次FFT之后的频谱谱线频率

直接读数，还是要x2
FFT每一个刻度之间的谱线频率间隔是：(ptps/saps)
假定我们识别谱线间隔是ptps/saps/2,这是最低频信号，实际建模试一下，参见附录A，

结论是：

FFT无论做几遍，频率成分都可以直接读取。频率轴的刻度在多次FFT变换中保持不变。

1.工况1 - double FFT

最低速部分能识别到5Hz。此时的采样长度是大概200ms。这个没有意义。我试试对采样数据做插值。

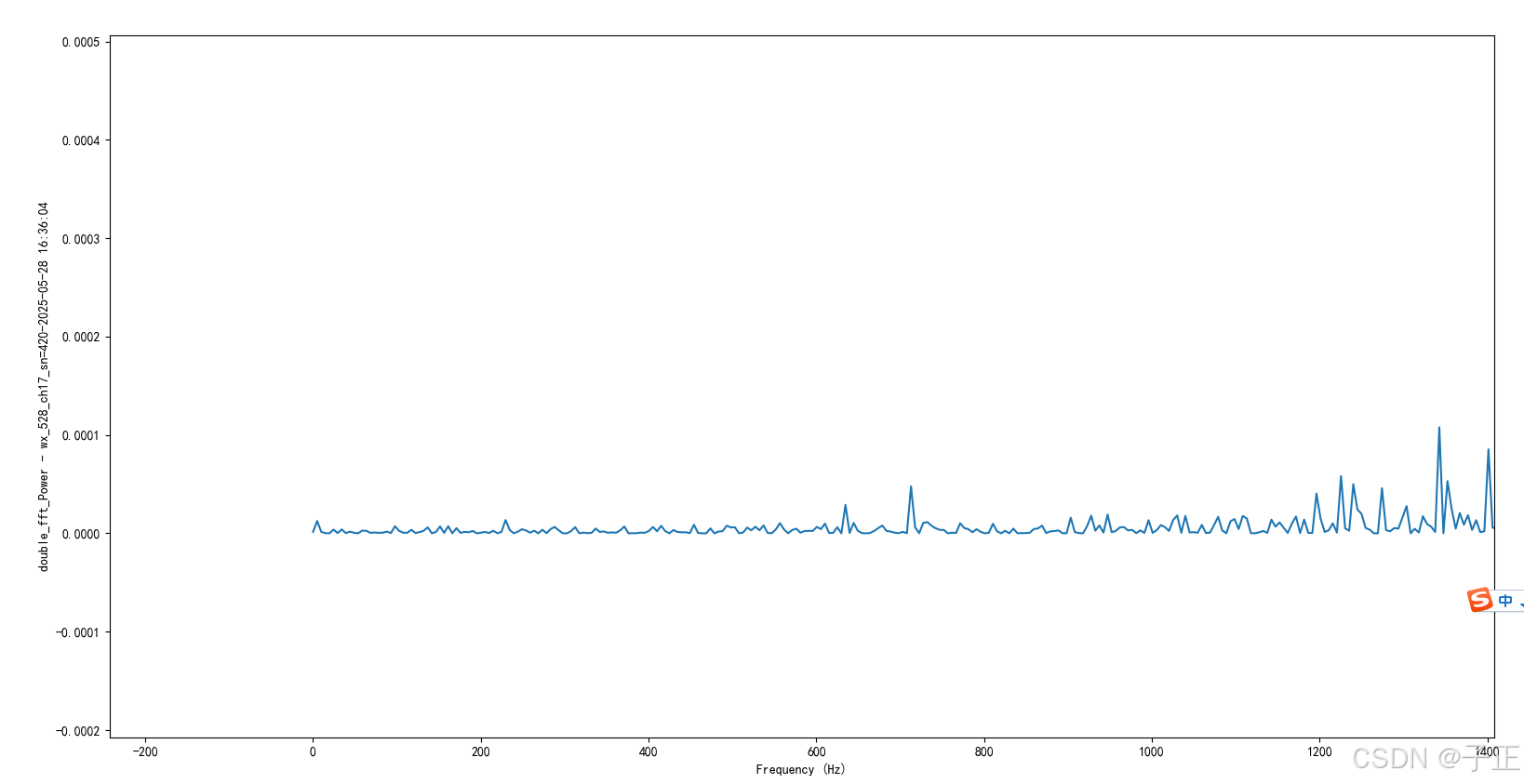
1.1 此时的代码：

        window = np.hamming(len(x_axis))
        windowed_data = floatSample * window
        fft_1st = np.fft.fft(windowed_data)
        windowed_data = fft_1st * window
        fft_2nd = np.fft.fft(windowed_data)
        fft_result = fft_2nd
        n = len(windowed_data)
        sampling_freq = 1//x_axis[1]  # 根据实际采样频率调整
        freqs = np.fft.fftfreq(n, 1/sampling_freq)
        power_spectrum = np.abs(fft_result)**2 / (sampling_freq * n)
        plt.plot(freqs[:n//2], power_spectrum[:n//2])
        plt.xlabel('Frequency (Hz)')
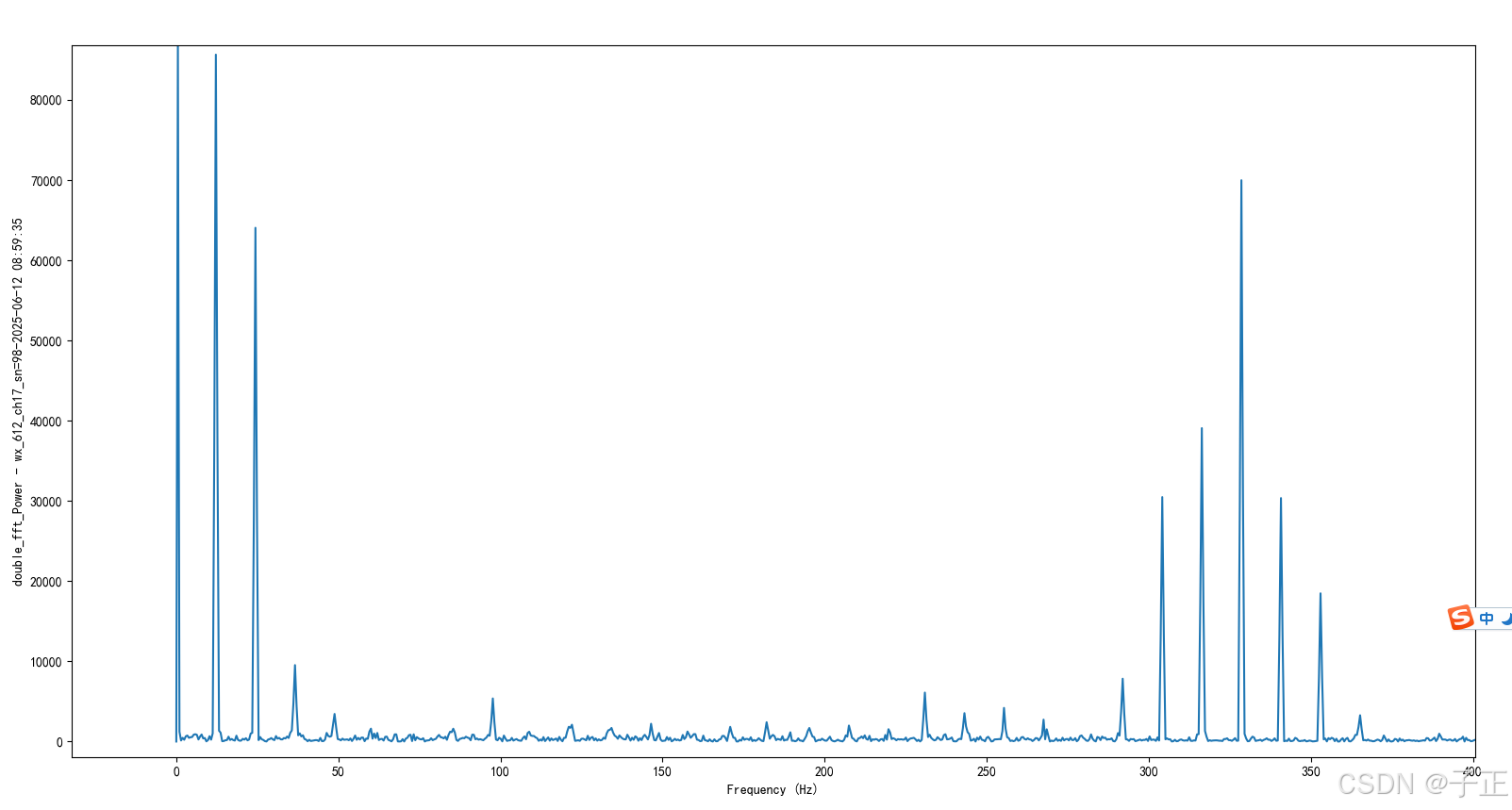
        plt.ylabel(f'double_fft_Power - {memo}-{timeSample}')
        plt.show()

2.工况1 - 前后补零至1:10之后的double FFT.

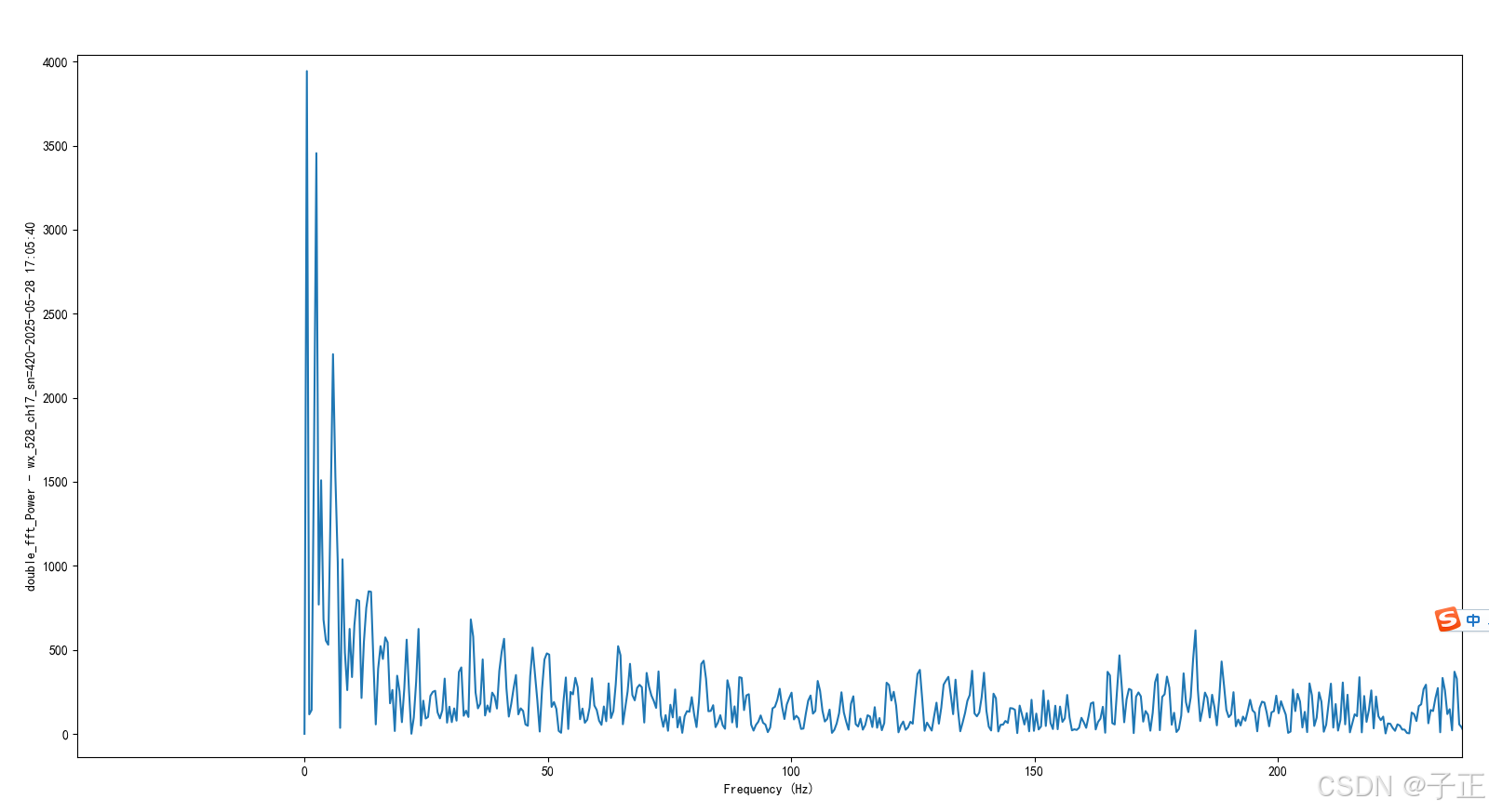
此时的虚拟采样时常已经扩大至2s，频谱分辨率是0.5Hz
输出已经抹掉了0Hz，
第一低频高峰是2.438Hz，对应的还是200ms(1/2.438e-3*2)，可忽略。
第二峰值：其他锋线【3.40Hz, 5.85Hz(max), 7.79Hz，9.26Hz】
按5.85Hz计算，此时转频 = 5.85*60 = 351rpm，此时似乎工作在25Hz电源频率。
3.40*60= 204Hz，它很像是电源的某种分频。4倍频。考虑此时25Hz的话，是电源的2倍频。
- 7.79Hz此时就很像电机的转差率谱线，此时的电机转差率是：0.0835
- 此时电机的基础转速应该是：701rpm
- 这和5.85Hz是匹配的。

在10Hz高频方向两个平顶锋，频点分别是：【10.96Hz, 13.41Hz】

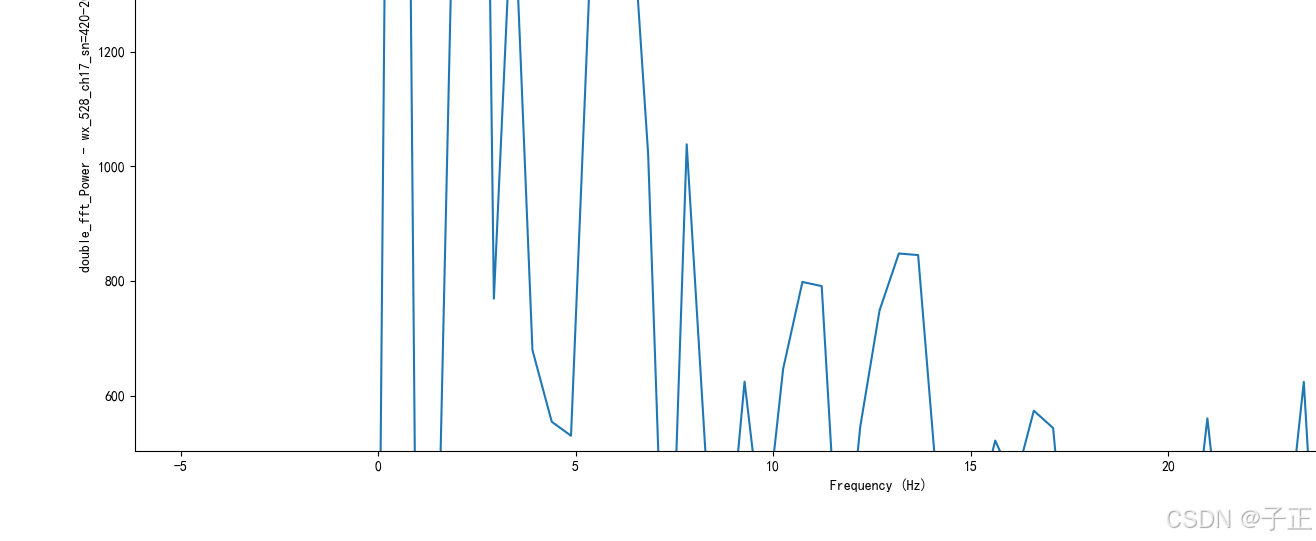
2.1 此时代码

第一轮fft不加窗大概也可以，第二轮必须加窗。

 # 计算补零参数
 target_length = 20480
 pad_total = target_length - len(x_axis)
 pad_before = pad_total // 2          # 前补零数
 pad_after = pad_total - pad_before   # 后补零数


 #double fft
 window = np.hamming(len(x_axis))
 windowed_data = floatSample * window
 # 执行补零
 arr_padded = np.pad(windowed_data, (pad_before, pad_after), 'constant', constant_values=0)
 plt.plot(arr_padded)
 plt.show()
 x_axis = [1/saps*sn for sn in range(0, len(u16Sample)*10)]
 window = np.hamming(len(x_axis))        
 fft_1st = np.abs(np.fft.fft(arr_padded))
 windowed_data = fft_1st * window
 
 fft_2nd = np.fft.fft(windowed_data) #fft必修加窗，第一次补0时可能不用。
 fft_result = fft_2nd
 fft_result[0] = 0
 n = len(windowed_data)
 sampling_freq = 1//x_axis[1]  # 根据实际采样频率调整
 freqs = np.fft.fftfreq(n, 1/sampling_freq)
 #power_spectrum = np.abs(fft_result)**2 / (sampling_freq * n)
 plt.plot(freqs[:n//2], np.abs(fft_result)[:n//2])
 plt.xlabel('Frequency (Hz)')
 plt.ylabel(f'double_fft_Power - {memo}-{timeSample}')
 plt.show()

3.校验：

这款振动信号的电机是：735rpm, 50Hz输入，30kW电机
变速比：50:1
所以735/50 = 14.7 Hz

所以，这种方法是有效的。

4.复核

4.1 一次严重噪声下的数据，同一设备。

这相当于有一个强的外部激励源作用下：

低频第一谱线：0.00Hz，忽略。
第2谱线：12.2Hz,如果换算成输出电机频率 = 12.2*60=732Hz，与电机额定转频很接近。
另一种计算方法是：先计算变速比：12.2Hz*50 *60=频率是20Hz

附录A FFT*2频率轴可以直接读数的证明

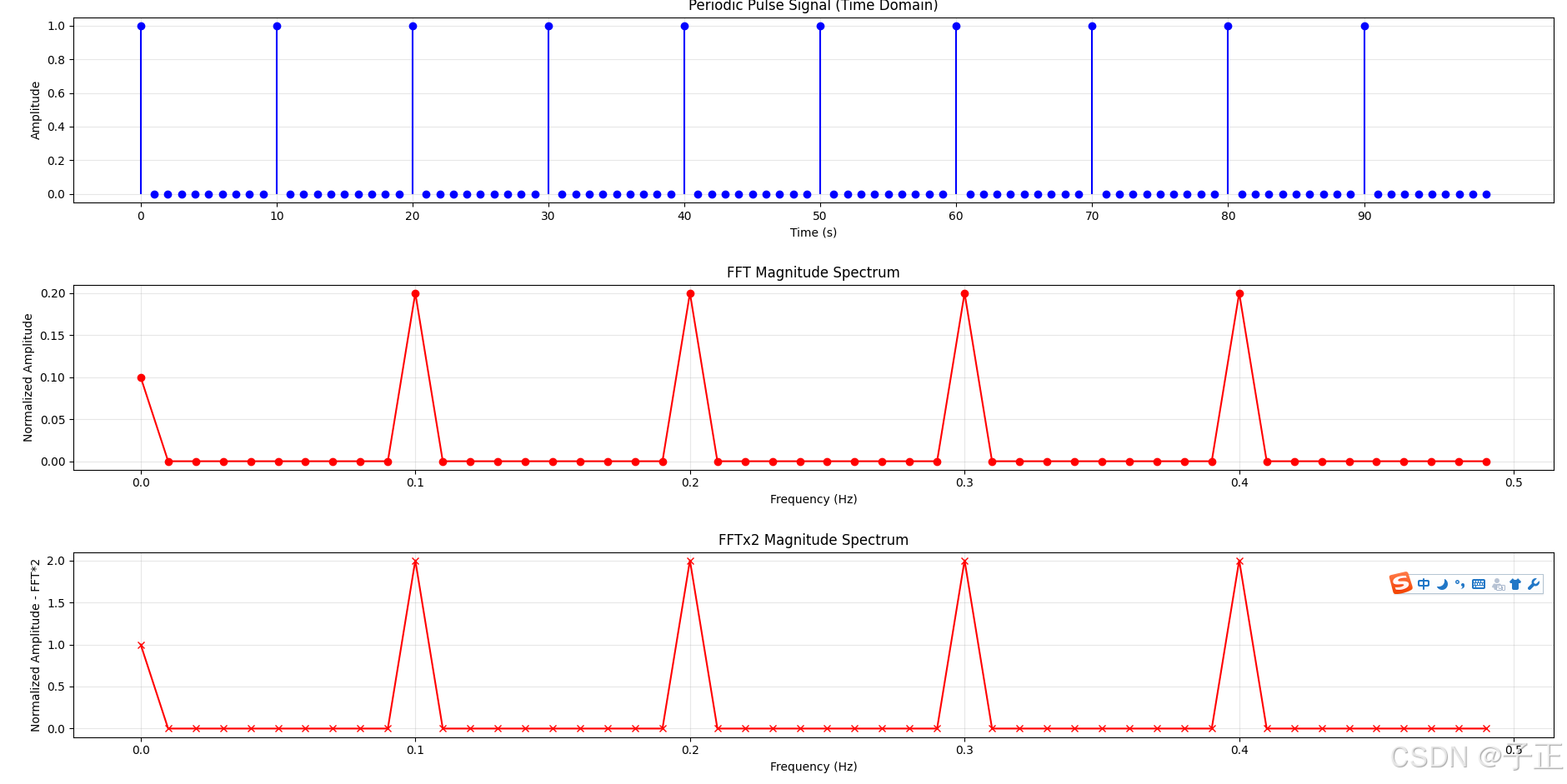
源码：

import numpy as np
import matplotlib.pyplot as plt

# 参数设置
fs = 1  # 采样率 = 1 Hz (每秒1个点)
N = 100  # 总点数 = 100
pulse_interval = 10  # 脉冲间隔 = 10个点

# 1. 生成脉冲信号
t = np.arange(N)  # 时间序列 [0, 1, 2, ..., 99] 秒
signal = np.zeros(N)
signal[::pulse_interval] = 1  # 每10个点设置一个脉冲（索引0,10,20,...,90）

# 2. 计算FFT
fft_result = np.fft.fft(signal)  # 复数频谱
freq = np.fft.fftfreq(N, d=1/fs)  # 频率轴 (Hz)
magnitude = np.abs(fft_result) / N * 2  # 幅度谱归一化 <cite data-id='30008'>30008</cite>
magnitude[0] /= 2  # 直流分量特殊处理 

# 3. 二次FFT
fft_result2 = np.fft.fft(fft_result)  # 复数频谱
magnitude2 = np.abs(fft_result2) / N * 2  # 幅度谱归一化 <cite data-id='30008'>30008</cite>
magnitude2[0] /= 2  # 直流分量特殊处理 

# 3. 可视化
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(12, 8))

# 时域信号
ax1.stem(t, signal, linefmt='b-', markerfmt='bo', basefmt=" ")
ax1.set_title("Periodic Pulse Signal (Time Domain)")
ax1.set_xlabel("Time (s)")
ax1.set_ylabel("Amplitude")
ax1.grid(alpha=0.3)
ax1.set_xticks(np.arange(0, N, 10))

# 频域幅度谱
positive_freq_mask = (freq >= 0) & (freq <= fs/2)  # 取正频率部分 (0~0.5 Hz)
ax2.plot(freq[positive_freq_mask], magnitude[positive_freq_mask], 'r-o')
ax2.set_title("FFT Magnitude Spectrum")
ax2.set_xlabel("Frequency (Hz)")
ax2.set_ylabel("Normalized Amplitude")
ax2.grid(alpha=0.3)
ax2.set_xticks(np.arange(0, 0.51, 0.1))

ax3.plot(freq[positive_freq_mask], magnitude2[positive_freq_mask], 'r-x')
ax3.set_title("FFTx2 Magnitude Spectrum")
ax3.set_xlabel("Frequency (Hz)")
ax3.set_ylabel("Normalized Amplitude - FFT*2")
ax3.grid(alpha=0.3)
ax3.set_xticks(np.arange(0, 0.51, 0.1))

plt.tight_layout()
plt.show()