量化不确定性的伟大探索：熵与香农的四大天才之举

关于贝叶斯主义那曲折动人的历史，需要讲一点关于 17 世纪的闲话很有好处，那正是布莱兹·帕斯卡和皮埃尔·德·费马终于尝试将概率这个概念数学化的时代。

来源 | 《贝叶斯的博弈：数学、思维与人工智能》

作者 | 黄黎原（Lê Nguyên Hoang）

译者 | 方弦

1

香农熵

量化不确定性可能看起来没什么用，甚至很荒谬。但是，掌握不确定性曾经在人类历史上肩负着重任：破译纳粹密码。在第二次世界大战期间，英国人艾伦·图灵和美国人克劳德·香农曾经为了交换密码学知识碰过面。香农和图灵当时似乎并没有怎么讨论密码学，但两人都理解了对不确定性进行量化的重要性。为此，图灵在战争期间引入了班伯里的计算，用以推断数段不同密文通过同一个恩尼格玛密码机配置加密得到的可能性的置信度。香农在这条道路上走得更远。

在 1948 年，香农发表了人类历史上最具影响力的论文之一，题为《通信的数学原理》（“A Mathematical Theory of Communication”）。这篇卓越的论文提出，可以利用概率分布来为某个信源发送的消息建模。用贝叶斯的术语来说，这就相当于考虑这个信源之后会发送的消息的先验概率分布。比如说，纳粹士兵很有可能在发送的消息中某处插入“希特勒万岁”，使用德语词汇，或者只发送“一切如常”的德语翻译。纳粹发送的消息是随机的，但远非任意的。

香农的第一个天才之举，就是将消息中的信息量等同于在贝叶斯置信度的视角下这一消息的稀有性。比如说“Lê”这个名字在欧洲就包含了许多信息，几乎可以等同于我。这是因为这个名字在欧洲非常罕见，正是这种稀有性让它能够传递大量信息。

反之，同一个名字在越南河内就几乎不包含任何信息，它能指向叫这个名字的几千甚至数十万越南人。这个词如此常见的事实意味着它带有的信息量很少。也就是说，一条消息中包含的信息只能相对于某个情景来衡量，更准确地说，是相对于某个用于评判信息出现概率的贝叶斯置信度体系而言。没有语境和质疑，概率检验就出问题。

香农的第二个天才之举，就是利用对数来量化消息中的信息量。为什么是对数？那是因为两条独立消息的信息量就是每条消息的信息量之和，但两条独立信息同时出现的概率是两者概率的乘积。要将乘积变成求和，我们必须用到相关的数学工具。这一工具就是对数。

更准确地说，对于出现概率为 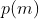 的信息 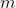，香农将其信息量定义为 。也就是说，这样的信息含有的信息量就是令 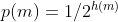 的指数 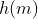。所以，出现概率非常小的信息拥有的信息量  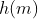很大。最后，香农推断出了信源的期望信息量  的公式，也就是这个信源发出的消息的平均信息量  ：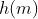

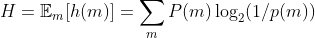
香农希望将  这个数量称为信源的期望信息量或不确定性函数。但最终他听从了约翰·冯·诺伊曼给他的建议：“你应该将它叫作熵，理由有两个。第一，你的这个不确定性函数在统计物理学中也会用到，用的就是这个名字，所以，它已经有名字了。第二，更重要的是，没有人真正知道熵是什么，所以在你任何论辩里都可以先发制人。”

熵的名字来源于物理学家鲁道夫·克劳修斯。通过引入名为熵的物理量，克劳修斯成功将这一原则转化为数学公式。热水和凉水混合起来会得到温水，其实就是说封闭系统的熵会上升。克劳修斯将后者提升到了“热力学第二定律”这个高度。

然而克劳修斯的熵仍然相当晦涩，没有被人理解。路德维希·玻尔兹曼的天才之处在于通过原子假设来定义熵，也由此砌下了统计力学的第一块砖。玻尔兹曼为他的定义感到非常自豪，甚至将它写在了自己的墓碑上面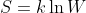：。这个方程说的是什么？首先要明白，我们有关热力学的测量仪器无法测量围绕着我们的  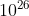个粒子的位置和速度，毕竟要做到这一点可需要千亿亿亿字节。与之相反，我们测量的热力学物理量，比如压力、温度、容积或质量，都概括了大量粒子的行为。我们说这些量是宏观量，与之相对的是直接来自粒子的微观量。

玻尔兹曼的智慧就在于注意到在宏观量已知的前提下，熵正好能够量化微观上的不确定性。更准确地说，玻尔兹曼证明了克劳修斯研究的熵 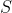 实际上相当于与宏观量相符合的微观状态个数  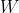的对数，两者之间只差了一个乘法常数 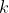，我们把它叫作玻尔兹曼常数。克劳修斯预言熵这个物理量的增加不可避免，但它不过是一种在完成宏观测量之后对依旧存在的微观不确定性的量化。

但香农的熵是不是真的与玻尔兹曼的熵一样？答案是肯定的，实际上，前者是后者的推广。为了理解这一点，我们必须意识到，在给定宏观量测量值的前提下，对于可能出现的不同微观状态，我们都拥有它的先验置信度。但玻尔兹曼证明了，在热力学平衡中与宏观量相容的所有 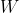 个微观状态出现的可能性都相等。因此，每个微观状态出现的概率都是 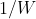。将香农方程中的  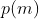换成 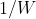 的话，我们就能得出在  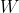个微观状态等可能出现的情况下，热力学系统的熵就是 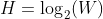。如果要使这些量的单位符合物理量的国际单位制的话，就必须乘以一个常数 。

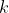香农确确实实推广了玻尔兹曼的熵。

2

香农的最优压缩

香农的第三个天才之举，就是理解了熵实际上衡量的是什么。看上去要多奇怪有多奇怪的是，熵衡量的实际上是消息的最优压缩。也就是说，它衡量的是将消息储存在硬盘上需要的最少比特数，或者说通过带宽有限的电缆传输这一消息所需的最短时间。香农实际上证明了我们无论如何都无法超越通过香农熵计算出来的根本限制。

为了理解香农熵和数据压缩之间的关系，我们考虑一下“猜猜是谁？”这个桌上游戏。在这个游戏中，每位玩家先在一组人物头像中选择一个，然后猜测对方选择的是哪一个头像。为此，玩家必须对另一位玩家提出如下形式的判断题：那个头像是男人吗？那个人戴眼镜吗？那个人头发长吗？玩家之间交替提问和回答，首先猜到对方选择的头像的人就胜出。

香农在 1948 年的论文中证明了，如果一共有 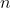 个头像可以选择，而且对手以随机等概率的方式选择了其中一个，那么平均来说必须至少问出  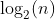道判断题才能确定对手选择的头像。此外，假设我们知道对手更经常选择男性头像而不是女性头像，而且更偏向于选择戴眼镜的头像，也就是说，如果我们对于对手的选择持有某种有根据的贝叶斯信念的话，那么香农的论文就证明了平均所需的问题数目至少等于对应的香农熵。

更厉害的是，香农熵对应着一种理想状态，其中对手给出的答案序列决定了他对头像选择的最优编码。更准确地说，香农提出的编码方法相当于给头像贴上由一串 0 和 1 组成的标签，0 代表否定回答，1 代表肯定回答。这样一来，如果对手对前两个问题的回答分别为“是”和“否”的话，那么最优编码的开头首先是 1，接下来是 0。于是，头像的身份就可以用一串 0 和 1 来代表，香农将其称为二进制数字（binary digit），或简称为比特（bit）。

香农在更普遍的情况下证明了所有通信都可以归结为一串由 0 和 1 组成的序列，因此通信能够通过数字化获益良多。这个结论可能今天看起来很显然，但当时并非如此，很多人仍然在模拟技术上押注。通过 1948 年的这篇论文，香农开启了数字时代。

2

香农冗余度

香农的第四个天才之举，就是证明了如何通过不完美的信道通信。在实践中，当人们用电信号将消息从 A 传递到 B 时，这一信号可能会轻易受到各种干扰。也许会变成 0，反之亦然。为了处理这个问题，香农的想法就是引入贝叶斯置信度，用以推断消息可能受到的干扰。然后香农证明了，只要这些贝叶斯置信度是正确的，那么这个非完美信道就等价于另一个完美信道，而这个完美信道的带宽等于非完美信道的带宽减去信道不完美性在某种意义上的熵。因此，只要加上足够多的冗余，任何信息都可以通过非完美信道传递。香农甚至对所需冗余进行了量化：消息在通过非完美信道传递时，所需冗余量应该大约等于消息受到的干扰的熵。

这些结论可能非常难以理解，但冗余是一个我们非常熟悉的现象，虽然人们一直都没有意识到这一点。当你跟朋友在吵闹的酒吧里讨论的时候，你们几乎不可能听到对方所说的全部内容。虽然如此，一般来说，我们也不需要听到对方所说的全部内容才能理解对方在说什么。这是因为，日常语言中的大部分词语对于句子含义的影响是次要的。即使把那些次要的句子成分去掉，“你轻松猜我话”（你也能轻松猜到我想说的话）。

法语拥有非常多的冗余，这也就解释了为什么英语文章通常比其法语译文更短，也解释了为什么法国人说话比英国人快。传递信息的带宽实际上差不多，因为即使法国人每秒说出的音节数比英国人更多，但比起英语，法语中每个音节包含更多的冗余，也就是包含更少的信息。

在今天，香农的所有概念，无论是比特、香农熵、信道容量还是冗余量，都已经成了信息技术的核心工具。但它们的应用远远超越了技术的领域。当然，我们不仅会在统计物理中遇到这些概念，它们被用于研究气体的状态演变；而且我们还会在语言学中看到，它们也被用于理解语言的演化，甚至在（地外）生物学中被用于探测智慧生命，因为它们的通信中包含的冗余可能与成年人类或海豚的交流中的冗余类似。一般正是语言的这种冗余性让我们能够补充别人的语句。地外生命所说的句子很可能也是如此，因为这些智慧生命大概也要想办法通过不完美的信道来交流。

  推荐阅读

《贝叶斯的博弈：数学、思维与人工智能》

作者：黄黎原

译者：方弦

法国数学类科普书、大学数学参考及教材类图书畅销书目，在机器学习、人工智能、逻辑学和哲学等众多领域中，探索贝叶斯定理蕴藏的智慧与哲理。

贝叶斯定理一旦与算法相结合，就不再是一套枯燥的数学理论或认识论，而变成了应用广泛的知识宝库，催生了众多现代数学定理，以及令人称道的实践成果。

02

《趣学贝叶斯统计：橡皮鸭、乐高和星球大战中的统计学》

作者：[美] 威尔·库尔特（Will Kurt）

译者：王凌云

本书用十余个趣味十足、脑洞大开的例子，将贝叶斯统计的原理和用途娓娓道来。你将从直觉出发，自然而然地习得数学思维。读完本书，你会发现自己开始从概率角度思考每一个问题，并能坦然面对不确定性，做出更好的决策。

03

《谁在掷骰子？不确定的数学》

作者：[英] 伊恩•斯图尔特

译者：何生

几个世纪以来，在好奇心以及精确预测未来的“野心”驱动下，具有开拓意识的数学家希望从概率论和统计学着手，减少各种“不确定性”。但他们发现，某些问题始终难以解决，而直觉也在不断误导人类。

本书探讨了关于“不确定性”的有趣故事和相关科学知识。知名科普作家伊恩·斯图尔特巧妙地建立起一个易于理解、充满想象力的数学框架，从概率论、统计学、贝叶斯方法、混沌理论等角度展现了“不确定性”在金融市场、天气预报、人口普查、医学、量子物理学和宇宙学等诸多领域中的重要作用，展望了与不确定性问题紧密相关的科学门类的广阔研究前景。

04

《贝叶斯数据分析（第2版）》

作者：约翰·K. 克鲁施克（John K. Kruschke）

译者：王芳

1.美国加州大学伯克利分校博士，特罗兰研究奖获得者，美国印第安纳大学心理学和脑科学名誉教授、统计学副教授约翰·K. 克鲁施克，拥有近25年的统计学教学经验总结！

2.极佳的贝叶斯统计入门书籍！如果你认为统计学很难，或许是因为你在入门时错过了本书。

3.原著豆瓣高达9.4分！全面覆盖实用的贝叶斯统计知识，可读性强！