为什么用卷积层而不用全连接层

全连接神经网络中使用了全连接层,在全连接层中,相邻层的神经元全部连接在一起,输出的数量可以任意指定.

全连接层存在什么问题呢?那就是数据的形状被忽视了,比如,输入数据是图像是,图像通常是长,宽,通道方向上的高三维形状,但是,在向全连接层输入时,需要将三维数据拉平为1维数据,比如下面的的网络:

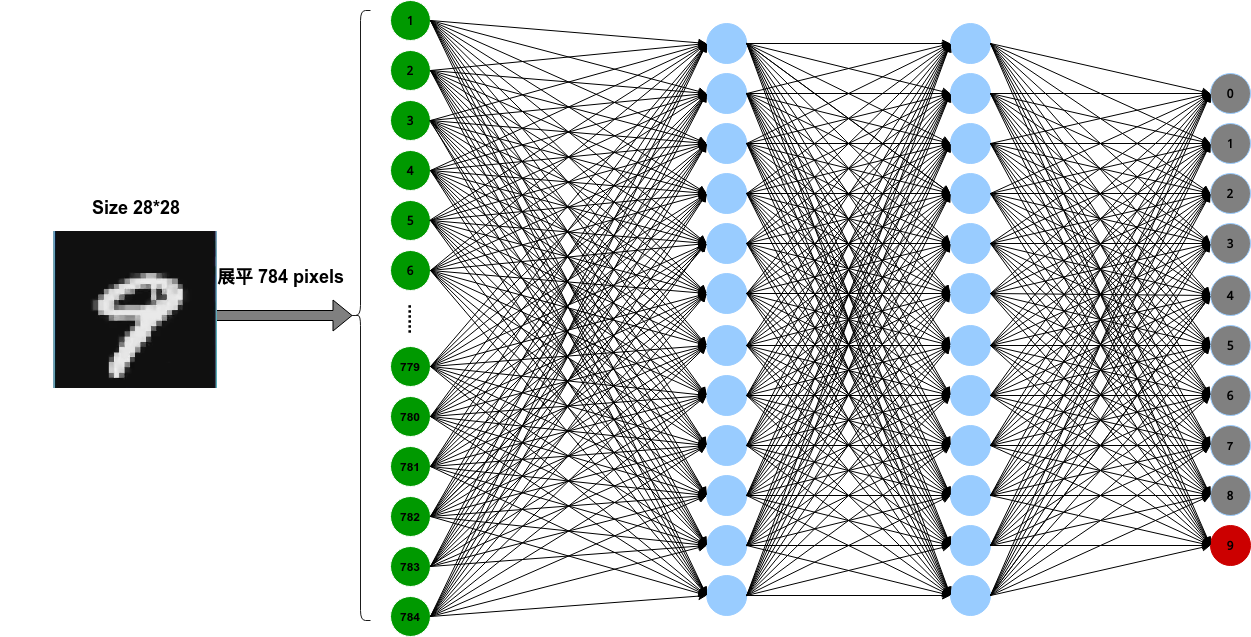
输入图像是1通道,长,宽均为28像素的形状,但是却被排列成了1列,784个数据的形式输入到最开始的网络层.

图像是三维形状,这个形状中应该含有重要的空间信息,比如,空间上临近的像素为相似的值,RGB的各个通道之间分别有密切的关联性,相距较远的像素之间没有什么关联等,3维形状中可能隐藏有值得提取的本质模式,但是,因为全连接层会忽视形状,将全部的输入数据作为相同的神经元(同一维度的神经元)处理,所以无法利用与形状相关的信息.

而卷积层可以保持形状不变,当输入数据是图像时,卷积层会以三维的数据形式接受输入数据,并且同样以3维数据的形式输至下一层,因此,在CNN中,可以正确理解具有形状的数据.

如下图:

 

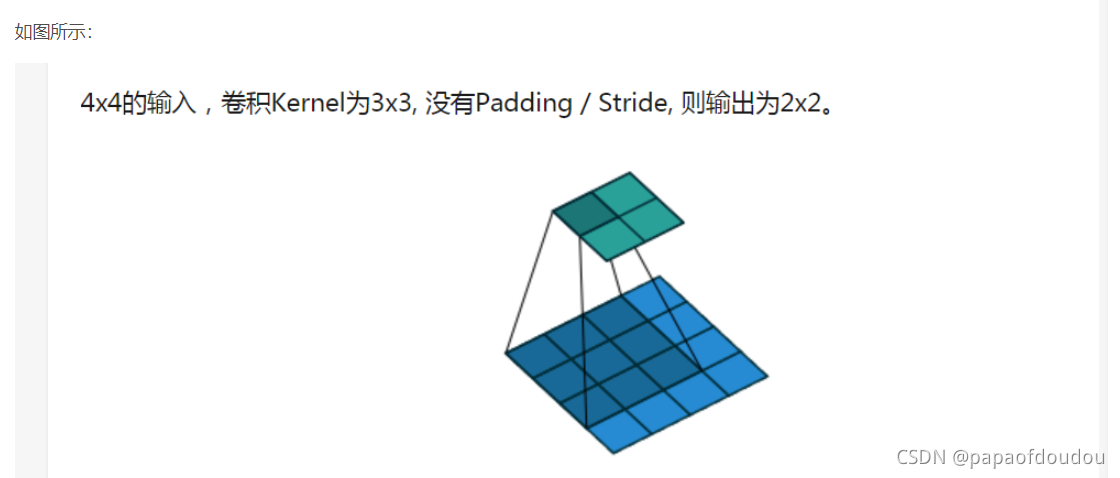
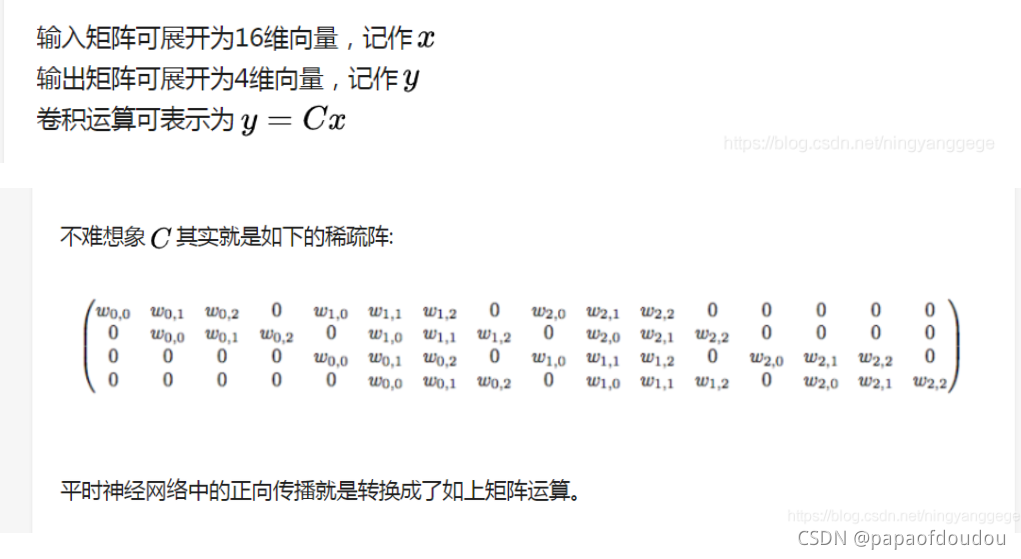
不但可以保留形状信息,而且会有效减小参数数量和链接数量,全连接的情况下,需要16*4=64个参数,但是经过卷积处理后,只需要9个参数需要学习,其它都为0.

卷积核和上一层的关系可以用下面的网络图来表示，注意局部连接和权值共享，每个输出像素都是3*3的连接，需要9个参数，而非卷积需要的4*4个连接，16个参数。另一方面降低了模型的复杂度，也就减小了过拟合的风险。

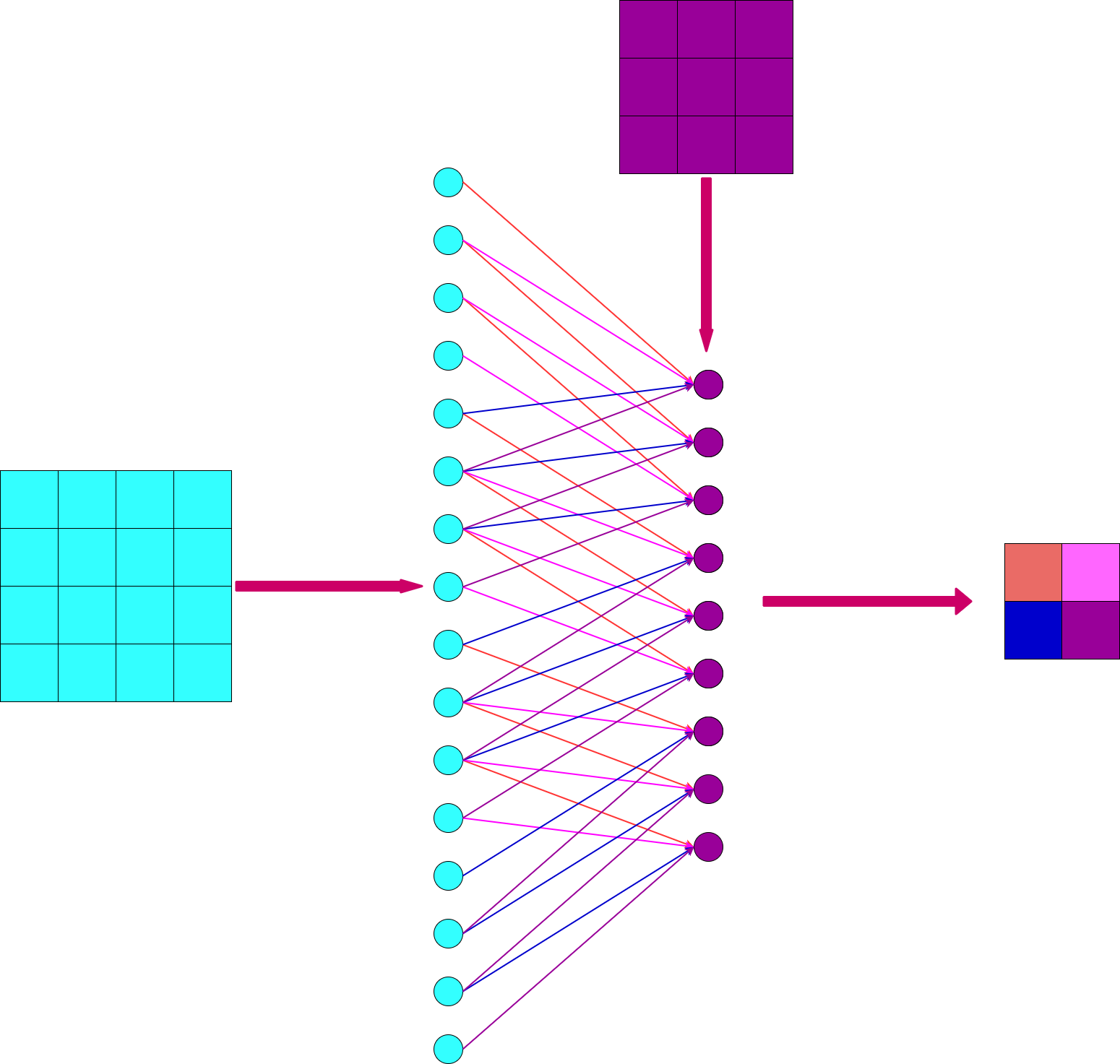
可以看到,在不加padding的情况下,输入图像边缘的四个像素只有一个连接.

这里说明一下为什么要引入卷积运算，尽管前面的矩阵乘法其实已经可以解决很多问题了，但是一旦到了图像领域，对一个 1920*1080 的图像做乘法，就是一个 [1, 2,073,600] 的列向量了，这个运算量已经不算小了，而用卷积操作，计算量就会大大缩减；另一方面，如果把一个二维的图像压缩成一个一维的向量，其实就丢失了像素点在上下左右方向相互关联的信息，例如一个像素点和周围的颜色通常比较相近，这些信息很多时候是很重要的图像信息。

卷积神经网络的特点：

1、它的神经元之间的连接是非全连接的；

2、它在同一层中某些神经元之间的连接的权重是共享的。

这种非全连接和权值共享的网络结构降低了网络模型的复杂度，减少了权值的数量，这种网络结构对平移、旋转、倾斜、比例缩放等具有高度不变性。

---

结束!