LBP算子介绍

原创已于 2025-11-07 20:10:36 修改 · 726 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #算法 #python #计算机视觉 #特征提取

于 2025-11-07 17:32:13 首次发布

计算机视觉（特征提取）专栏收录该内容

3 篇文章

订阅专栏

前言

LBP（Local Binary Pattern）

中文名称为局部二值模式，它是一种用来描述局部特征纹理的算子。它的核心是解决图像纹理相关的识别、分类、分割、与异常检测问题。

这里主要讲的内容为LBP的基本原理和其计算提取特征步骤、改进方法和相关代码实现。

LBP算子的核心思想

原始LBP算子的核心思想和原理是

在算子定义的邻域内（如3*3），以领域中心像素为基准，用周围的8个像素的灰度值与其进行比较，若周围某个像素的灰度值大于中心像素标记为1，反之为0。这样我们就能通过比较在这个3*3的邻域内得到八个由0和1组成的数，接下来从领域的左上角开始顺时针对这些数字进行排列，得到一个二进制数字。这个二进制数字就是中心像素的LBP值。中心像素的LBP值反映了该像素周围区域的纹理信息。

LBP值计算图解

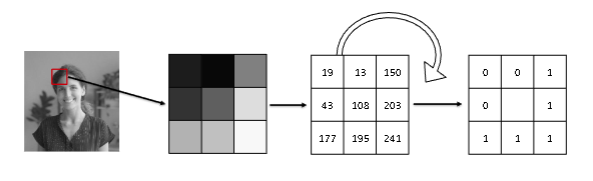
图片来源：华为人才在线

LBP算子使用的具体步骤

对一幅图像进行特征向量的提取，可以分为四个步骤：

1.提取每个像素的LBP值。

首先图像的每个像素的灰度值提出来，在每个3*3的领域中，然后将中心像素灰度值与周围8个像素的灰度值进行比较。大于中心像素灰度值的标记为1反之标记为0。再将标记后的八个由0和1组成的数自左上角开始顺时针进行排序得到一个二进制数。最后将这个二进制数转换为十进制。以此得到该像素的LBP值。

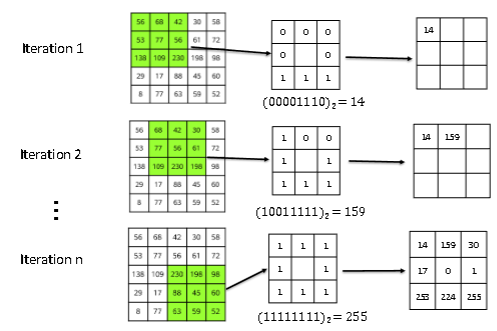
图像来源华为人才在线

2.将图像分为多个块（Block）。

得到LBP特征图像后，将LBP特征图像划分为多个块（Block），通常情况会将LBP特征图像分为8行8列，共64块区域。

通过灵活的对块大小的定义可以更便捷的提取特征图像里的特征。

其主要优点为：增强局部特征表达能力、保留空间结构信息、提升分类或识别性能、适应多尺度分析需求。

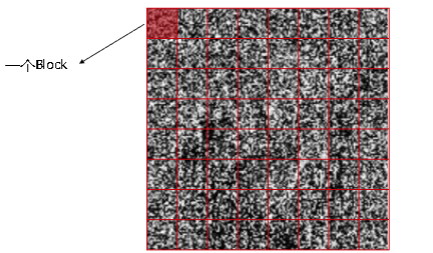
图片来源：华为人才在线

3.统计每个块（Block）中LBP的直方图。

计算各区域特征图像的直方图时，横轴代表LBP值。以原始LBP算子为例，其LBP值为8位二进制数，因此直方图横轴取值范围为0到255，共256个区间（Bin）。纵轴表示各LBP值出现的频数。为便于后续处理，通常会对纵轴进行归一化处理。最终得到的1×256维数据即为该区块的LBP描述子。

a.直方图是什么？

是统计离散数据分布的工具，此处专门统计“一个块（Block）中所有像素的LBP值编码的分布情况”

具体来说：Block 内每个像素都有一个 LBP 编码（如 8 位编码对应 0-255 共 256 种可能），直方图会统计每种编码出现的次数（或归一化后的频率），最终形成一个长度为 “编码种类数” 的数值序列（即直方图向量）

b.LBP描述子是什么？

本质是表征图像特征的结构化数据，是计算机能理解、可计算的 “特征语言”。

在 LBP 的 Block 直方图步骤中，描述子就是 “每个 Block 对应的 LBP 直方图向量”—— 比如 8 位经典 LBP 的直方图有 256 个维度，每个维度的值代表该 Block 内对应 LBP 编码（0-255）出现的次数 / 频率，向量整体就承载了这个 Block 的纹理特征。

c.该步骤的核心目的

降维与信息聚合：单个像素的 LBP 编码是离散的点特征，直接用所有像素的编码进行后续计算（如匹配）会产生巨大计算量。通过 Block 直方图，将一个 Block 内成百上千个像素的编码，聚合为一个固定长度的向量，大幅降低数据维度。

增强鲁棒性：单个像素的 LBP 编码易受噪声、微小位移影响（比如像素轻微偏移可能导致编码突变）。直方图统计的是 “编码分布”，对局部微小变化不敏感，能提升特征的稳定性。

提供可比特征：直方图向量是结构化数据，可通过计算向量间的距离（如欧氏距离、余弦距离），快速判断两个 Block（或两幅图像的 Block 集合）的纹理相似度 —— 这是后续分类、识别任务的核心基础。

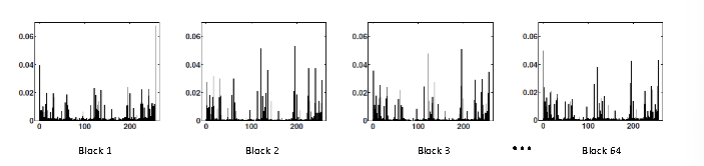
图片来源：华为人才在线

4.将所有直方图连接成特征向量。

将所有的Block的描述子，按空间的顺序依次排列成一行，形成LBP特征向量。特征向量可供Adaboost等机器学习进行训练。

流程示意图：

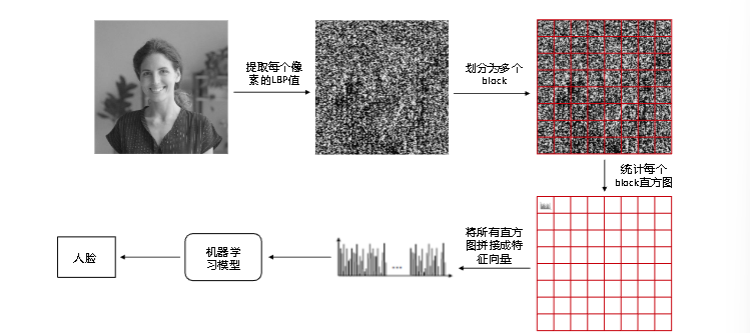
图片来源：华为人才在线

原始LBP算子的特点（AI）

优势特点

编码简单，计算高效：基于 3×3 窗口内 8 个邻域像素与中心像素的灰度比较，生成 8 位二进制编码（共 256 种模式），计算逻辑直观，时间复杂度低，适合实时性要求较高的场景。
对光照变化鲁棒：因依赖相对灰度关系而非绝对灰度值，当图像整体光照均匀变化时，LBP 编码能保持稳定，在光照不稳定的场景（如户外监控）中优势明显。

局限特点

对旋转敏感：邻域像素的比较按固定方向（如顺时针）进行，图像旋转后，编码会完全改变，无法适应旋转场景下的纹理识别需求。
窗口尺度固定：仅采用 3×3 局部窗口，只能捕捉微小区域的纹理细节，对大尺度纹理或需要多尺度分析的场景（如复杂纹理的图像分类）表现力不足。
特征维度冗余：256 维的直方图包含大量稀疏模式（部分编码出现频率极低），且未考虑模式的语义关联性（如旋转后的相似模式被视为不同类），导致特征维度高、信息利用率低。

LBP算子的改进（AI）

为了克服原始 LBP 算子的局限、提升其性能，可从旋转不变性、尺度适应性、特征精简性、多模态融合等维度进行改进，以下是关键改进方向及方法：

1. 解决 “旋转敏感” 问题：旋转不变 LBP（RI-LBP）

原理：对原始 LBP 编码进行循环移位，取所有移位结果中的最小值作为最终编码。例如，原始编码10100001循环移位后可能得到01010001、10100010等，取其中最小的十进制值作为该纹理的旋转不变编码。
优势：图像旋转后，同一纹理的编码保持一致，大幅提升对旋转场景的鲁棒性（如旋转后的人脸识别、纹理分类）。

2. 解决 “尺度固定” 问题：多尺度与圆形 LBP

多尺度 LBP：采用不同大小的邻域窗口（如 3×3、5×5、7×7）分别计算 LBP，再将多尺度的直方图拼接，捕捉不同尺度的纹理细节（适用于复杂纹理的图像分类，如区分不同粗细的织物）。
圆形 LBP（Circular LBP）：突破正方形窗口限制，按圆形邻域选取像素（如半径为R的圆上均匀取P个像素），通过双线性插值处理非整数坐标的像素灰度。例如，LBPP,R表示在半径R的圆上取P个像素的 LBP，可灵活适配不同尺度的纹理（如大纹理用P=16,R=8，细纹理用P=8,R=2）。

3. 解决 “特征冗余” 问题：统一模式 LBP（Uniform LBP）

原理：统计 LBP 编码中跳变次数（0→1 或 1→0 的次数），若跳变次数≤2，则定义为 “统一模式”，否则为 “非统一模式”。例如，8 位 LBP 中，00000000（0 次跳变）、00000001（1 次跳变）、00000011（1 次跳变）等属于统一模式，其余为非统一模式。
优势：将原始 256 种模式精简为约 59 种统一模式（+1 种非统一模式汇总），大幅降低特征维度，同时保留纹理的主要语义信息（实验表明，90% 以上的自然纹理由统一模式构成）。

4. 多模态与空间增强：融合其他特征与空间结构

多通道 LBP：在彩色图像中，对 RGB 三个通道分别计算 LBP，或在灰度图像中结合梯度、边缘等特征，形成多通道 LBP 直方图，丰富特征表达（如用于彩色纹理分类、复杂场景的目标检测）。
空间金字塔 LBP：将图像划分为多个层级的块（如先分大区块，再细分小区块），每个块计算 LBP 直方图后拼接，增强对空间结构的捕捉能力（适用于需要空间信息的任务，如人脸识别、场景分类）。

5. 结合机器学习优化：特征降维与选择

对 LBP 直方图进行主成分分析（PCA）或线性判别分析（LDA），进一步降维并突出类间差异，提升后续分类 / 识别的效率与准确率。
采用稀疏编码或深度学习（如将 LBP 作为 CNN 的输入或特征层），让模型自动学习更具判别力的 LBP 特征表示。

这些改进方法可根据具体任务需求组合使用（如 “旋转不变 + 统一模式 + 圆形 LBP”），从而在旋转鲁棒性、尺度适应性、计算效率、特征判别力等方面全面提升 LBP 算子的性能。

代码实现：（python）

ef LBP(image):
    width,height = image.shape             #获取图像的长宽
    res = np.zeros((width-2,height-2))     #存放返回的LBP特征值
    xx = [-1,  0,  1, 1, 1, 0, -1, -1]
    yy = [-1, -1, -1, 0, 1, 1,  1,  0]   #xx, yy 用于获取相对中心点的位置，得到邻接点坐标值.
    for i in range(1,width-1):
        for j in range(1,height-1):
            temp = ""                    #存放当前像素值的LBP特征值
            for m in range(8):
                Xtemp = xx[m] + i    
                Ytemp = yy[m] + j        #分别获得对应坐标点
                if image[Xtemp, Ytemp] > image[i, j]:   #像素比较
                    temp = temp + '1'
                else:
                    temp = temp + '0'
            res[i - 1][j - 1] =int(temp,2)  #将二进制字符串转换为十进制整数，写入结果
    print('二进制数为：{}'.format(temp))
    print('转换后的十进制为：{}'.format(res[0,0]))
    print(res)
    return res