LBP算子分类和基本思想
1. LBP算子的背景
LBP算子又称为Local Binary Pattern,是一种用来描述图像局部纹理特征的算子,由于其具有灰度不变性、旋转不变性等显著优点,得以被广泛应用。LBP的另一个优点就是思想比较好理解,并且计算过程不复杂,简单易懂,这样产生的时间复杂度在可计算范围内。LBP多用于人脸识别方面,由于其对纹理识别很精细,相比较于缺陷检测,也是一个很好的方向,由于作者最近再做关于图像缺陷检测方面的文章,为了能够熟记其思想并准确掌握,决定用写博客的方式巩固,若哪位仁兄发现写的不好的地方,请及时纠正!!!
2. LBP的几种分类
- 基本LBP算子
LBP算子的基本思想就是最大化每个像素点与周围像素点之间的关系,或是大于或是小于,这样可以让局部特征更明显的表现。主要思想:设(x,y)是我们要处理的像素矩阵中的任意一个像素点,就像下面这个表格,选择3*3矩阵对中心像素点进行处理。
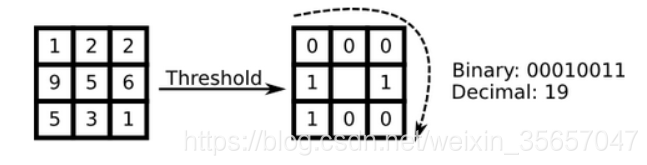
如上表所示,分别将(x,y)周围的像素点与(x,y)进行比较,假设记(x,y)点像素值为γ,如果周围像素值小于γ,则标记其在矩阵中的位置信息为0,否则标记为1(这里的0,1标记不是唯一的,也可以小于标记为1,大于标记为0)。这样就能得到一个0、1值得矩阵,也就是二值矩阵。
可以看到,经过比较赋值之后的二值矩阵可以构成一个8位得二进制数,我们可以按照丛左上角为最高位,右下角作为最低为的标准,那么我们把这个二进制数值叫做LBP特征值,那么以8位作为最基本的周围像素点取值标准,如上图,生成的二进制数组就是00010011,得到的LBP特征值就是19。
- 圆形LBP算子
上述LBP算子方法很简单,但是缺点也很明显,就是覆盖区域是固定的,只是周围的8个,对于求多个尺度多个方向的纹理需要就显得十分笨拙,为了适应不同尺度的纹理特征,并达到灰度和旋转不变性的要求,由此提出了圆形(circle)LBP算子,这是一种根据半径和角度设计的LBP算子,可以得到多种尺度、角度的纹理特征。
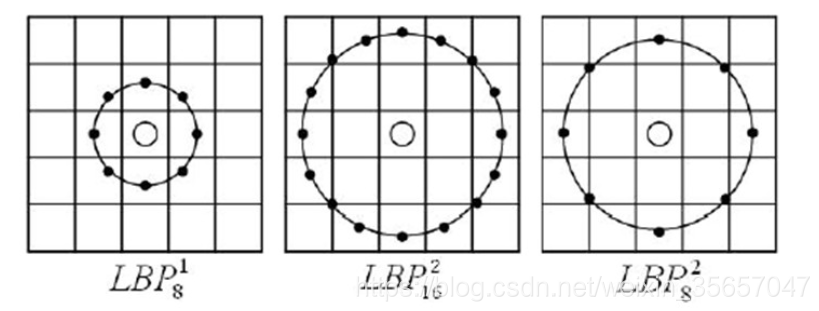
其基本思想如上图,根据半径和方向选择中心点周围的像素点的值
,以上图第一个图为例子,我们将半径选为1,周围像素点个数选择8个(可以选择任意多个),方向是Π/4,那么这里面的周围像素值的计算就要用到插值法,我采用的是双线性插值求像素值。
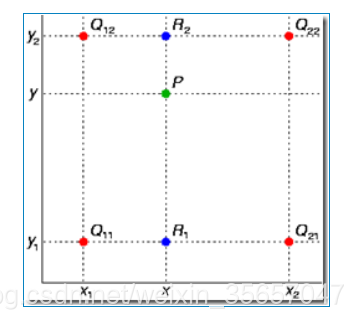
如上图所示,P点就是我们要求的像素点,而P点并不在像素矩阵上,所以我们采用周围像素值估计中心像素值法,周围位于矩阵上的像素点分别是Q12,Q22,Q11,Q21,我们设Q11=(x1,y1),Q12=(x1,y2),Q21=(x2,y1),Q22=(x2,y2),首先X方向进行线性插值,得到
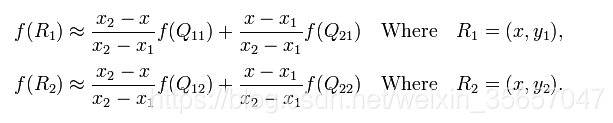
我们现在已经计算出R1和R2两个点的像素值,再用一个插值法就能得到P点像素值,
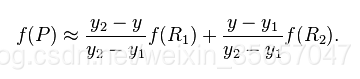
这样我们就可以计算出P点的像素值,由于我们采用上述方法直接计算的话,过程十分繁琐并且计算量比较大,所以我们可以采用坐标系统的方法,选择一个坐标系统,将P点周围的四个值当作(0,0),(0,1),(1,0),(1,1),然后我们可以这样计算:
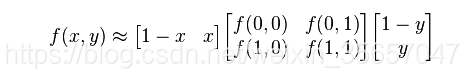
上面就是双线性插值计算的方法,先计算X或者Y轴都可以。 - 等价模式LBP算子
一个LBP算子可以产生很多种不同的二进制模式,对于上述我们采用的半径为1,采样点8的LBP算子,会产生2^8个模式,对于采用数2的n次幂,会产生这样就会产生冗余信息,同样对于纹理的识别和提取也是非常不利的,所以我们会采用一种叫做等价模式的方法对产生的所有模式进行缩减,Ojala最先提出等价模式的思想。Ojala等认为,在实际图像中,绝大多数LBP模式最多包含两次从1到0或从0到1的跳变。因此,Ojala将“等价模式”定义为:当某个LBP所对应的循环二进制数从0到1或从1到0最多两次跳变时,该LBP所对应的二进制数组就称为一个等价模式类。例如00000000,11111111都是0次跳变,而01111110,00001000都是两次跳变。除邓加模式类以外的模式都归为另一类,称为混合模式类。
通过这种方式进行改进之后,可以很有效的减少二进制模式类,模式数量由2^n减少到n(n-1)+2,这样可以很有效的减少冗余度,这使得特征向量的维数变少,减少高频噪声带来的影响,鲁棒性增强。 - 旋转不变LBP算子
由上诉可知,上面的LBP算子具有灰度不变性,这是由于每个像素点的LBP特征值跟周围像素点有必要关系的,所以即使亮度值发生变化,不会改变周围像素值对中心像素点的影响,但是却不具备旋转不变性,由此提出来了一种基于旋转不变的LBP算子。
旋转不变LBP算子的特征如下图所示:
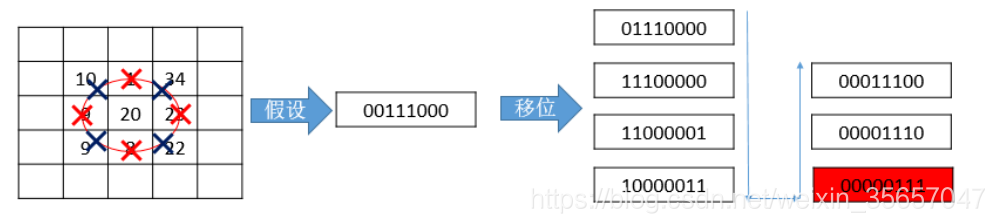
假设我们产生的二进制数组是00111000,那么我们可以经过移位操作,选择移位过程中最小的那个数,来代表最终的特征,如上图,最后的特征值就是00000111。
3. LBP实现算法
- 基本LBP
void Normal_LBP(Mat& src, Mat &dst) //通常LBP图
{
// 循环处理图像数据
for (int i = 1; i < src.rows - 1; i++)
{
for (int j = 1; j < src.cols - 1; j++)
{
uchar tt = 0;
int tt1 = 0;
uchar u = src.at<uchar>(i, j);
if (src.at<uchar>(i - 1, j - 1) > u) { tt += 1 << tt1; }
tt1++;
if (src.at<uchar>(i - 1, j) > u) { tt += 1 << tt1; }
tt1++;
if (src.at<uchar>(i - 1, j + 1) > u) { tt += 1 << tt1; }
tt1++;
if (src.at<uchar>(i, j + 1) > u) { tt += 1 << tt1; }
tt1++;
if (src.at<uchar>(i + 1, j + 1) > u) { tt += 1 << tt1; }
tt1++;
if (src.at<uchar>(i + 1, j) > u) { tt += 1 << tt1; }
tt1++;
if (src.at<uchar>(i + 1, j - 1) > u) { tt += 1 << tt1; }
tt1++;
if (src.at<uchar>(i - 1, j) > u) { tt += 1 << tt1; }
tt1++;
dst.at<uchar>(i - 1, j - 1) = tt;
}
}
}
- 圆形LBP
void Circle_LBP(Mat& src, Mat &dst, int radius, int neighbors) //圆形算子LBP函数
{
for (int n = 0; n < neighbors; n++)
{
// 采样点的计算
float x = static_cast<float>(-radius * sin(2.0*CV_PI*n / static_cast<float>(neighbors)));
float y = static_cast<float>(radius * cos(2.0*CV_PI*n / static_cast<float>(neighbors)));
// 上取整和下取整的值
int fx = static_cast<int>(floor(x));
int fy = static_cast<int>(floor(y));
int cx = static_cast<int>(ceil(x));
int cy = static_cast<int>(ceil(y));
// 小数部分
float ty = y - fy;
float tx = x - fx;
// 设置插值权重
float w1 = (1 - tx) * (1 - ty);
float w2 = tx * (1 - ty);
float w3 = (1 - tx) * ty;
float w4 = tx * ty;
// 循环处理图像数据
for (int i = radius; i < src.rows - radius; i++)
{
for (int j = radius; j < src.cols - radius; j++)
{
// 计算插值
float t = static_cast<float>(w1*src.at<uchar>(i + fy, j + fx) + w2 * src.at<uchar>(i + fy, j + cx) + w3 * src.at<uchar>(i + cy, j + fx) + w4 * src.at<uchar>(i + cy, j + cx));
// 进行编码
dst.at<uchar>(i - radius, j - radius) += ((t > src.at<uchar>(i, j)) || (std::abs(t - src.at<uchar>(i, j)) < std::numeric_limits<float>::epsilon())) << n;
}
}
}
}
- 等价模式LBP
void getUniformPatternLBPFeature(Mat &src, Mat &dst, int radius, int neighbors)
{
//基于Uniform Pattern形式的LBP圆形算法,这是一种
//具有旋转不变性,尺度不变性,并且另一个很好的特点是不基于亮度值改变
//补充,还包含旋转不变性
//等价模式+旋转不变+LBP
//Mat src = _src.getMat();
//LBP特征图像的行数和列数的计算要准确
//_dst.create(src.rows - 2 * radius, src.cols - 2 * radius, CV_8UC1);
dst.create(src.rows - 2 * radius, src.cols - 2 * radius, CV_8UC1);
//dst.create(src.rows - radius, src.cols - radius, CV_8UC1);
//选择在像素矩阵的基础上沿边界去掉2*radius,防止溢出
dst.setTo(0); //将dst矩阵像素值都设为0
//LBP特征值对应图像灰度编码表,直接默认采样点为8位
//直接对256中编码表进行压缩存储,可以分为无跳变、1次跳变、2次跳变、和其他情况(归一),这样
//简化下来,可以压缩到59种模式,减少冗余
uchar temp = 1;
uchar table[256] = { 0 };
for (int i = 0; i < 256; i++)
{
if (getHopTimes(i) < 3)
{
table[i] = temp;
temp++;
}
}
//是否进行UniformPattern编码的标志
bool flag = false;
//计算LBP特征图,一共有8个点(默认设置),一共八个角度
for (int k = 0; k < neighbors; k++)
{
if (k == neighbors - 1)
{
flag = true;
}
//计算采样点对于中心点坐标的偏移量rx,ry
//坐标确定公式,横纵坐标分别是:R * cos(角度) R * sin(角度)
float rx = static_cast<float>(radius * cos(2.0 * CV_PI * k / neighbors));
float ry = -static_cast<float>(radius * sin(2.0 * CV_PI * k / neighbors));
//为双线性插值做准备
//对采样点偏移量分别进行上下取整
//floor函数是向下取整,ceil函数是向上取整
int x1 = static_cast<int>(floor(rx));
int x2 = static_cast<int>(ceil(rx));
int y1 = static_cast<int>(floor(ry));
int y2 = static_cast<int>(ceil(ry));
//根据公式进行映射计算,分别将求得像素点周围最近的四个点来进行双线性插值估算,这时
//将四个点分别映射到(0.0),(0.1),(1.0),(1.1)这四个位置上
//将坐标偏移量映射到0-1之间
//rx和ry分别为其坐标的整数
float tx = rx - x1;
float ty = ry - y1;
//根据0-1之间的x,y的权重计算公式计算权重,权重与坐标具体位置无关,与坐标间的差值有关
float w1 = (1 - tx) * (1 - ty);
float w2 = tx * (1 - ty);
float w3 = (1 - tx) * ty;
float w4 = tx * ty;
//循环处理每个像素
for (int i = radius; i < src.rows - radius; i++)
{
for (int j = radius; j < src.cols - radius; j++)
{
//获得中心像素点的灰度值
uchar center = src.at<uchar>(i, j);
//根据双线性插值公式计算第k个采样点的灰度值
float neighbor = src.at<uchar>(i + x1, j + y1) * w1 + src.at<uchar>(i + x1, j + y2) * w2
+ src.at<uchar>(i + x2, j + y1) * w3 + src.at<uchar>(i + x2, j + y2) *w4;
//LBP特征图像的每个邻居的LBP值累加,累加通过与操作完成,对应的LBP值通过移位取得
dst.at<uchar>(i - radius, j - radius) |= (neighbor > center) << (neighbors - k - 1);
//进行LBP特征的UniformPattern编码
if (flag)
{
dst.at<uchar>(i - radius, j - radius) = table[dst.at<uchar>(i - radius, j - radius)];
}
}
}
}
}
- 旋转不变LBP
//进行旋转不变处理
for (int i = 0; i < dst.rows; i++)
{
for (int j = 0; j < dst.cols; j++)
{
unsigned char currentValue = dst.at<uchar>(i, j);
unsigned char minValue = currentValue;
for (int k = 1; k < neighbors; k++)
{
//循环左移
unsigned char temp = (currentValue >> (neighbors - k)) | (currentValue << k);
if (temp < minValue)
{
minValue = temp;
}
}
dst.at<uchar>(i, j) = minValue;
}
}
总结
上述过程就是我所学习到的东西,分享给大家,希望有帮助!!!




















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








