本文探讨了求解线性方程组Ax=b的情况，包括齐次线性方程组和非齐次线性方程组。当b=0时，若A的秩R(A)=n，方程有唯一零解；若R(A)<n，方程有无穷多解。对于非齐次线性方程组，当R(A)=R(B)时有解，且R(A)=R(B)=n时解唯一，R(A)=R(B)<n时解无穷。求解过程包括将方程化为阶梯型，求特解和零空间。
b=0时，为齐次线性方程组。R（A）=n时，即A的行列式D不为0，有唯一零解；R(A)<n时，即D=0，无穷多解。
b不为0，非齐次线性方程组，R(A）=R(B)增广矩阵时，方程有解，否则方程无解。R(A)=R(B)=n，有唯一零解；R(A)=R(B)<n，无穷解。
求解Ax=b：可解性和解的结构
对于求解Ax=b，首先我们要判断：
① 是否有解？
② 若有解，解是否唯一？
先化为阶梯型：
求解Ax=b的过程：
① 求出一个特解(Particular solution)：
设所有自由变量(Free variable)为０；
解出Ax=b的主变量(Pivot variable。
② 求出零空间
③ Ax=b的解为特解+零空间。
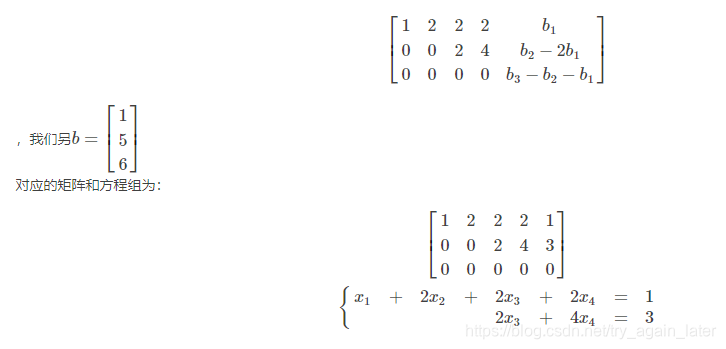
1、求特解：
2、第二步：求出零空间。
A求出简化行阶梯形式R得到
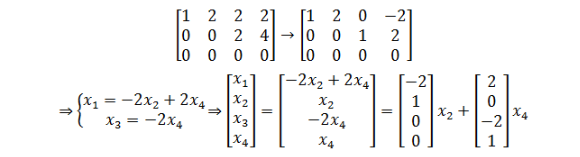
重点参考：
https://www.cnblogs.com/bigmonkey/p/9662057.html
https://blog.youkuaiyun.com/MadBam_boo/article/details/80138638
https://blog.youkuaiyun.com/stranger_man/article/details/80852095
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
