Zero-Inflated Log-Normal Loss

在营销LTV预测任务中，用户的价值呈现出如下特点：

1. 零膨胀（Zero-inflation）：大量用户的LTV为零（比如没有转化、没有付费）
2. 偏态分布：有转化的人群中，LTV的非零值分布通常呈现出右偏重尾（分布的右侧有更长的尾巴，且均值 > 中位数 > 众数），即呈对数正态分布（Log-Normal）

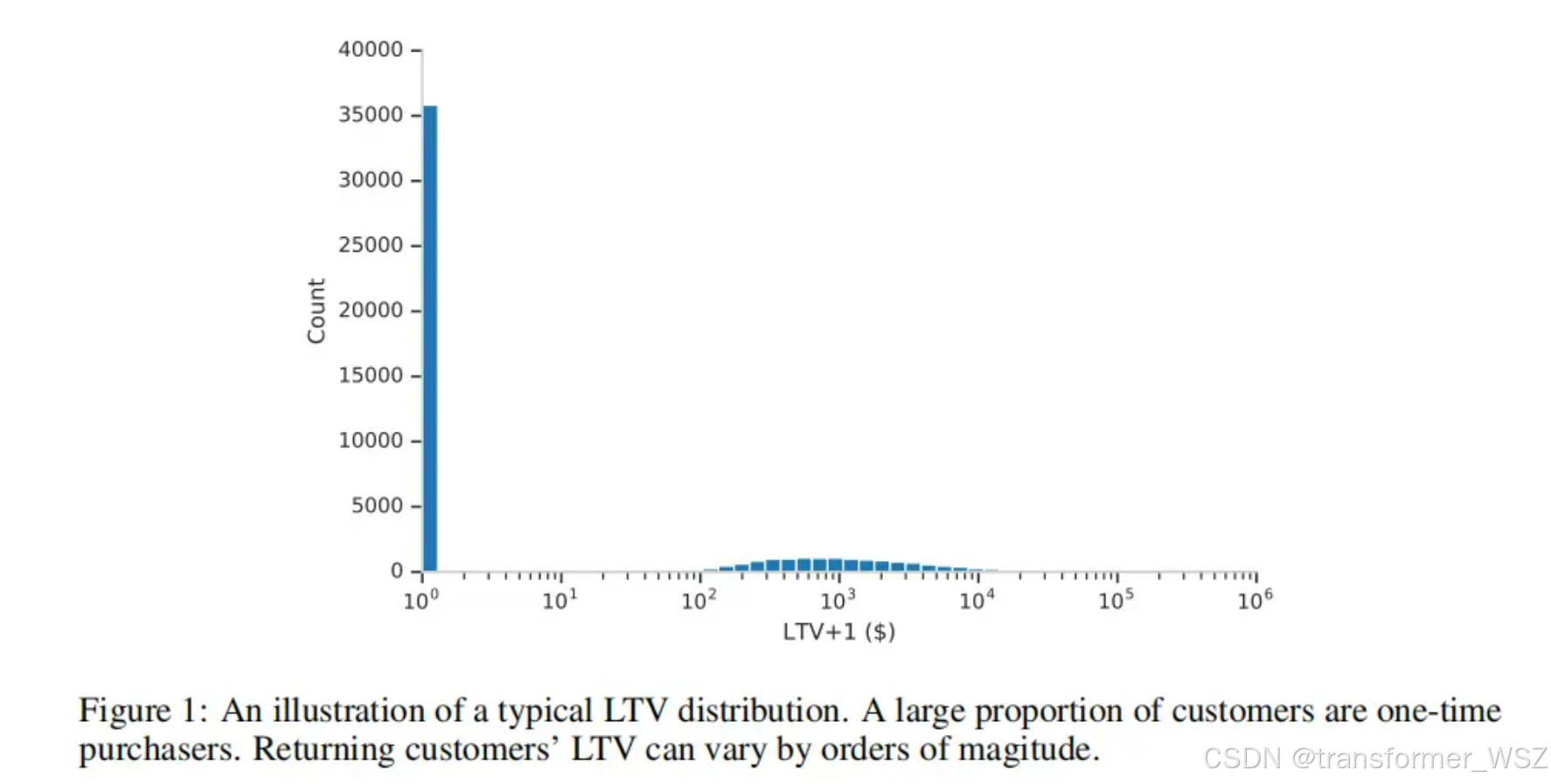
针对这种数据分布，Google提出了ZILN Loss，用于更真实地拟合这类零膨胀、长尾的数据。

LTV建模如下两个任务：用户是否付费、付多少费，分别对应上述两个问题。

$$pred\_ltv(x)=pay\_prob(x)\times pay\_amount(x)$$

问题1是个二分类任务，问题2则是个回归任务：

L ZILN  ( x ; p , μ , σ ) = L CrossEntropy  ( 1 { x > 0 } ; p ) + 1 { x > 0 } L Lognormal  ( x ; μ , σ ) L Lognormal  ( x ; μ , σ ) = log ⁡ ( x σ 2 π ) + ( log ⁡ x − μ ) 2 2 σ 2 \begin{aligned} L_{\text {ZILN }}(x ; p, \mu, \sigma) &= L_{\text {CrossEntropy }}\left(\mathbb{1}_{\{x>0\}} ; p\right)+\mathbb{1}_{\{x>0\}} L_{\text {Lognormal }}(x ; \mu, \sigma) \\ L_{\text {Lognormal }}(x ; \mu, \sigma) &= \log (x \sigma \sqrt{2 \pi})+\frac{(\log x-\mu)^2}{2 \sigma^2} \end{aligned} LZILN ​(x;p,μ,σ)LLognormal ​(x;μ,σ)​=LCrossEntropy ​(1{x>0}​;p)+1{x>0}​LLognormal ​(x;μ,σ)=log(xσ2π ​)+2σ2(logx−μ)2​​

具体到模型建模，就是学习$p$、$mu$、$sigma$：

以下是tensorflow的实现代码：

def zero_inflated_lognormal_loss(labels: tf.Tensor,
                                 logits: tf.Tensor) -> tf.Tensor:
  """Computes the zero inflated lognormal loss.

  Usage with tf.keras API:

  model = tf.keras.Model(inputs, outputs)
  model.compile('sgd', loss=zero_inflated_lognormal)

  Arguments:
    labels: True targets, tensor of shape [batch_size, 1].
    logits: Logits of output layer, tensor of shape [batch_size, 3].

  Returns:
    Zero inflated lognormal loss value.
  """
  # [0, 1.2, 3, 0], 0表示未付费，1.2表示付费金额
  labels = tf.convert_to_tensor(labels, dtype=tf.float32)
  positive = tf.cast(labels > 0, tf.float32)

  logits = tf.convert_to_tensor(logits, dtype=tf.float32)
  logits.shape.assert_is_compatible_with(
      tf.TensorShape(labels.shape[:-1].as_list() + [3]))

  # p
  positive_logits = logits[..., :1]
  classification_loss = tf.keras.losses.binary_crossentropy(
      y_true=positive, y_pred=positive_logits, from_logits=True)

  # mu, sigma
  loc = logits[..., 1:2]
  scale = tf.math.maximum(
      tf.keras.backend.softplus(logits[..., 2:]),
      tf.math.sqrt(tf.keras.backend.epsilon()))
  # 下面两行可以直接改成：log_prob(labels[labels>0])
  safe_labels = positive * labels + (
      1 - positive) * tf.keras.backend.ones_like(labels)
  regression_loss = -tf.keras.backend.mean(
      positive * tfd.LogNormal(loc=loc, scale=scale).log_prob(safe_labels),
      axis=-1)

  return classification_loss + regression_loss

---

参考

• LTV预估的一些思考
• Google用户付费预估深度模型笔记