机器学习详解(25):批标准化、层标准化、组标准化和实例标准化

在深度学习的训练过程中，标准化技术对于模型性能和训练稳定性至关重要。随着网络层数的增加和模型复杂度的提升，不同的标准化方法应运而生，每种方法都针对特定的问题和应用场景。

1 标准化

为了能够在不同的深度学习任务中选择最合适的标准化策略，提升模型性能并加速训练收敛。了解四种常用的标准化工作原理、适用场景和实际应用非常有必要。

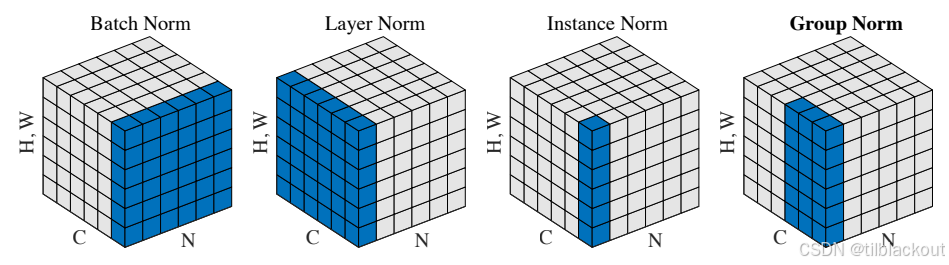
1.1 Batch Normalization(批标准化)

批标准化是在每个mini-batch内对特征进行标准化。具体来说，对于网络中的每一层，BN会计算当前batch中所有样本在每个特征维度上的均值和方差，然后使用这些统计量对特征进行标准化。标准化公式为：
$$\hat{x}=\frac{x-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$$

• ${\mu }_B$和${\sigma }_B^2$分别是当前batch的均值和方差，$ϵ$ 是防止除零的小常数。

问题

• Batch Size依赖性：当batch size较小时，batch内的统计量估计不准确，会导致训练不稳定。
• 训练与推理不一致：训练时使用batch统计量，推理时使用全局统计量，这种差异可能导致性能下降。
• 分布式训练复杂性：在多GPU训练中，需要跨设备同步统计量，增加了通信开销和实现复杂度。

1.2 Layer Normalization(层标准化)

层标准化是为了解决BN在序列模型中的问题而提出的。与BN不同，LN对每个样本的所有特征维度计算均值和方差，然后进行标准化。对于输入 $x\in {\mathbb{R}}^H$，层标准化的计算公式为：
$$\hat{x}=\frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}$$

• $\mu$和${\sigma }^2$是同一样本内所有特征的均值和方差。

层标准化主要解决了以下问题：

• 序列长度变化：在RNN和Transformer等序列模型中，输入序列长度可能不同，LN能够很好地处理这种变化。
• Batch Size无关性：LN的计算完全独立于batch size，使得单样本推理和小batch训练都能保持稳定。
• 训练推理一致性：由于只依赖单个样本的统计量，训练和推理时的行为完全一致。

1.3 Group Normalization(组标准化)

组标准化旨在结合BN和LN的优势。GN将通道分成若干组，然后在每组内计算均值和方差进行标准化。

对于输入特征图，GN首先将C个通道分成G组，每组包含$\frac{C}{G}$个通道，然后在每组内计算统计量：
$$\hat{x}=\frac{x-{\mu }_g}{\sqrt{{\sigma }_g^2+ϵ}}$$

• ${\mu }_g$和${\sigma }_g^2$是组内的均值和方差。

组标准化主要解决了以下问题：

• 小Batch训练：在目标检测、图像分割等任务中，由于内存限制，batch size通常很小，GN在这种情况下表现优异。
• 视觉特征相关性：通过对相关通道进行分组，GN能够更好地利用视觉特征间的相关性，特别适合卷积神经网络。

1.4 Instance Normalization(实例标准化)

实例标准化对每个样本的每个通道分别计算均值和方差进行标准化。可以看作是Group Normalization的特殊情况，其中每个通道自成一组。

对于输入特征图 $x\in {\mathbb{R}}^{N\times C\times H\times W}$，它的公式为：
$$\hat{x}\ast nchw=\frac{x\ast nchw-{\mu }_{nc}}{\sqrt{{\sigma }_{nc}^2+ϵ}}$$

• ${\mu }_{nc}$和${\sigma }_{nc}^2$是第n个样本第c个通道的均值和方差： $${\mu }_{nc}=\frac{1}{HW}\sum _{h=1}^H\sum _{w=1}^W{x}_{nchw}$$, $${\sigma }_{nc}^2=\frac{1}{HW}\sum _{h=1}^H\sum _{w=1}^W(x_{nchw}-{\mu }_{nc}{)}^2$$

实例标准化主要解决了以下问题：

• 风格独立性：通过对每个通道单独标准化，IN能够去除特定的风格信息，保留内容信息，这对风格迁移任务极其重要。
• 对比度标准化：IN能够标准化每个通道的对比度，使得网络更关注相对特征而非绝对数值。
• 快速风格化：在实时风格迁移中，IN能够快速消除原始图像的风格，为应用新风格提供干净的基础。
• 领域适应：在某些计算机视觉任务中，IN有助于减少不同数据源之间的域差异。

2 例子

假设我们在训练CNN做图像分类，输入了一个包含2张图片的batch：样本1为一张猫的图片，样本2为一张狗的图片。这两张图片经过几层卷积后，到达某个卷积层的输出，形状为 [2, 4, 2, 2]：2个样本，4个通道(特征图)，特征图大小(2×2)。

原始数据示例：

猫图片(样本1)的4个特征图：
特征图1: [[1, 2],     特征图2: [[5, 6],     特征图3: [[9, 10],     特征图4: [[13, 14],
         [3, 4]]              [7, 8]]              [11, 12]]             [15, 16]]

狗图片(样本2)的4个特征图：
特征图1: [[17, 18],   特征图2: [[21, 22],   特征图3: [[25, 26],   特征图4: [[29, 30],
         [19, 20]]            [23, 24]]            [27, 28]]            [31, 32]]

这里的数字代表该位置的特征激活值，不同的图片会在这些特征图上有不同的激活模式。

四种标准化方法的具体处理

批标准化

相同位置的数据一起计算均值和方差：

特征图1位置[0,0]: 猫图片=1, 狗图片=17 → 计算均值(1+17)/2=9, 用来标准化这个位置的特征
特征图1位置[0,1]: 猫图片=2, 狗图片=18 → 计算均值(2+18)/2=10, 用来标准化这个位置的特征
... 以此类推每个位置

所有图片在相同特征图的相同位置进行比较，标准化后每个位置的特征值都相对于该位置在整个batch中的分布。

• 训练阶段，BN 用 batch 内的统计量是为了拟合真实分布；推理阶段改用训练时累计下来的全局均值和方差，是为了保持推理结果一致性和稳定性。
  • 推理时只能处理一张图(或小batch)，样本太少，统计量不稳定

层标准化

把每个样本的所有数据放在一起计算均值和方差：

猫图片所有特征: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
计算这16个数的均值μ₁和方差σ₁，然后用 (x - μ₁)/σ₁ 标准化猫图片的所有特征

狗图片所有特征: [17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32]
计算这16个数的均值μ₂和方差σ₂，然后用 (x - μ₂)/σ₂ 标准化狗图片的所有特征

每张图片的所有特征都相对于这张图片的整体激活水平进行标准化，猫图片和狗图片分别独立处理。

组标准化

把通道分成几组，每组内部计算均值和方差。假设分成2组：组1=[特征图1,特征图2], 组2=[特征图3,特征图4]：

猫图片-组1特征: [1, 2, 3, 4, 5, 6, 7, 8]  (特征图1和特征图2的所有数据)
计算均值μ₁₁和方差σ₁₁，标准化这8个数

猫图片-组2特征: [9, 10, 11, 12, 13, 14, 15, 16]  (特征图3和特征图4的所有数据)
计算均值μ₁₂和方差σ₁₂，标准化这8个数

组1可能包含低级特征(边缘、纹理)，组2可能包含高级特征(形状、模式)，这样可以保持不同类型特征的相对独立性。

实例标准化

对每个样本的每个通道分别计算均值和方差：

猫图片-特征图1: [1, 2, 3, 4] → 计算均值μ₁₁=2.5, 方差σ₁₁, 标准化这4个数
猫图片-特征图2: [5, 6, 7, 8] → 计算均值μ₁₂=6.5, 方差σ₁₂, 标准化这4个数
猫图片-特征图3: [9, 10, 11, 12] → 计算均值μ₁₃=10.5, 方差σ₁₃, 标准化这4个数
猫图片-特征图4: [13, 14, 15, 16] → 计算均值μ₁₄=14.5, 方差σ₁₄, 标准化这4个数

狗图片同样每个特征图单独处理...

每个通道的特征都相对于该通道在当前样本中的分布进行标准化，完全独立于其他通道和其他样本。

3 方法对比与选择指南

下面是这三种标准化的对比：

特征维度	Batch	Layer	Group	Instance
标准化范围	在batch维度上，对每个特征通道进行标准化	在特征维度上，对每个样本的所有特征进行标准化	在通道组维度上，对每个样本的通道分组进行标准化	在每个通道维度上，对每个样本的每个通道单独标准化
计算统计量	使用整个batch的均值和方差	使用单个样本的均值和方差	使用单个样本中每个组的均值和方差	使用单个样本中每个通道的均值和方差
主要优势	在大batch场景下效果最佳，广泛验证	适合序列模型，不受序列长度影响	平衡了BN和LN的优势，适合视觉任务	完全去除风格信息，适合风格迁移和生成任务

常用场景的选择如下：

应用场景	Batch Normalization	Layer Normalization	Group Normalization	Instance Normalization
CNN图像分类	首选(大batch时)	效果一般	推荐(小batch时)	不推荐
目标检测	可用但batch size通常较小	不推荐	强烈推荐	不推荐
图像分割	可用但batch size限制	不推荐	强烈推荐	不推荐
风格迁移	不推荐	不推荐	可用	强烈推荐
图像生成（GAN）	可能影响生成质量	推荐	推荐	推荐(特别是生成器)
超分辨率	可用	可用	推荐	推荐
Transformer	不适合	标准选择	可用但不常见	不推荐
RNN/LSTM	不适合变长序列	推荐	可用但不常见	不推荐
扩散模型	可用但不常见	可用	广泛使用	推荐
领域适应	可用	可用	推荐	推荐
强化学习	取决于具体算法	通常更稳定	视觉RL中推荐	特定任务中推荐

• 批归一化：适合CNN图像分类等任务，batch size较大、数据分布稳定的场景
• 层归一化：适合NLP和Transformer模型中，尤其是序列长度变化大、batch size小的情况
• 组归一化：适合生成模型、风格迁移、batch size很小时，稳定性强、效果好
• 实例归一化：适合风格迁移、图像生成、艺术化处理等任务，能够有效去除图像的风格信息而保留内容结构，特别适用于需要标准化图像对比度和亮度、消除域差异的场景

4 总结

随着深度学习技术的不断发展，标准化方法也在持续演进。理解这些方法的原理和适用场景，将有助于在复杂的实际应用中做出最佳选择，从而构建更加高效和稳定的深度学习模型。