UVA10012 How Big Is It?【全排列+回溯】

Ian’s going to California, and he has to pack his things, including his collection of circles. Given a set of circles, your program must find the smallest rectangular box in which they fit.
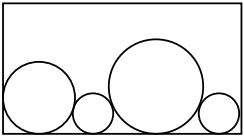
    All circles must touch the bottom of the box. The figure below shows an acceptable packing for a set of circles (although this may not be the optimal packing for these particular circles). Note that in an ideal packing, each circle should touch at least one other circle (but you probably figured that out).

Input
The first line of input contains a single positive decimal integer n, n ≤ 50. This indicates the number of lines which follow. The subsequent n lines each contain a series of numbers separated by spaces. The first number on each of these lines is a positive integer m, m ≤ 8, which indicates how many other numbers appear on that line. The next m numbers on the line are the radii of the circles which must be packed in a single box. These numbers need not be integers.
Output
For each data line of input, excluding the first line of input containing n, your program must output the size of the smallest rectangle which can pack the circles. Each case should be output on a separate line by itself, with three places after the decimal point. Do not output leading zeroes unless the number is less than 1, e.g. 0.543.
Sample Input
3
3 2.0 1.0 2.0
4 2.0 2.0 2.0 2.0
3 2.0 1.0 4.0
Sample Output
9.657
16.000
12.657

问题链接：UVA10012 How Big Is It?
问题简述：（略）
问题分析：
    给定m个圆的半径，求其排列的最小长度。
    这个问题首先用置换函数枚举所有的圆排列顺序（全排列），然后计算其最小长度。这个题解没有剪枝，需要改进。
    计算的关键是算出圆心的距离，如下图所示：

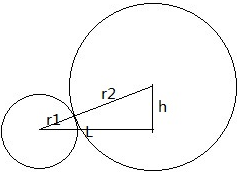
其中，h=r2-r1，L = sqrt( (r1+r2)^2-(r1-r2)^2)
程序说明：（略）
参考链接：（略）
题记：（略）

AC的C++语言程序如下：

/* UVA10012 How Big Is It? */

#include <bits/stdc++.h>

using namespace std;

const int M = 8;
double r[M], center[M], res, res2, ans;
int m;

void search(int k)
{
    if(k != m) {
        double tmp;
        res = 0;
        for(int i = 0; i < k; i++) {
            tmp = 2 * sqrt(r[i] * r[k]);
            tmp += center[i];
            tmp = max(tmp, r[k]);
            res = max(res, tmp);
        }

        center[k] = res;
        res2 = max(res2, center[k] + r[k]);
        search(k + 1);
    }
}

void cal()
{
    ans = 1e60;
    do {
        res2 = r[0] * 2;
        center[0] = r[0];
        search(1);
        ans = min(ans, res2);
    } while(next_permutation(r , r + m));
}

int main()
{
    int n;
    scanf("%d", &n);
    while(n--) {
        scanf("%d", &m);
        for(int i = 0; i < m; i++)
            scanf("%lf", &r[i]);

        sort(r, r + m);

        if(m == 1)
            ans = r[0] * 2;
        else
            cal();

        printf("%.3lf\n", ans);
    }

    return 0;
}