一文彻底搞懂Transformer - FFNN（前馈神经网络）

多层感知机

FFNN模型表达式： FFNN(x) = max(0, xW1 + b1)W2 + b2 (2)

在前馈神经网络中，权重（W）和偏置（b）是两个非常重要的参数，它们决定了神经元之间的连接强度和神经元的输出。

权重（W）：权重是神经网络中的连接参数，用于描述不同神经元之间的连接强度。在神经网络的前向传播过程中，输入数据会与权重进行加权求和，从而影响神经元的输出。权重的大小和正负决定了输入数据对输出数据的影响程度。

偏置（b）：偏置是神经网络中的一个附加参数，用于调整神经元的输出。偏置的作用类似于线性方程中的截距项，它使得神经元的输出可以偏离原点。偏置的存在使得神经网络能够学习更加复杂的函数关系。

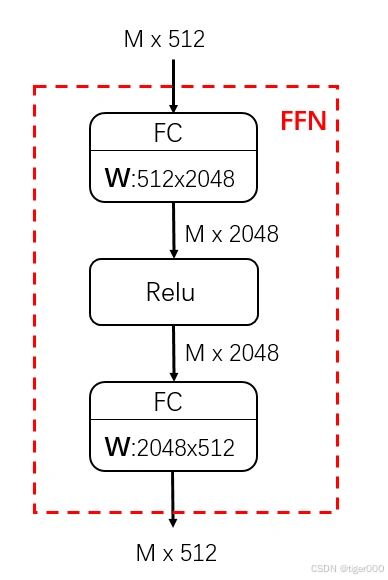
因为 FFN 层由两个线性变换层（FC）和一个非线性激活函数（ReLU）组成，通过在两个 FC 中间添加非线性变换（这是非常常见的操作），可以增加模型的表达能力，使模型能够捕捉到复杂的特征和模式。

但很多时候512维不够用，我们希望模型可以提取出更多维度的特征，于是，通过 FFN 两个相邻 FC 层的运算，可以将 512 维扩展到2048维（ FFN 的隐层），随后再降维到512维作为 FFN 的输出。

这种维度的一升一降，带来了两个变化：

增加了两个可学习的权值矩阵，也就是上面表达公式中的两个 W 矩阵。通过和权值矩阵的相乘将输入 512 维度向量映射到隐层的 2048 维度空间中，使得输入数据可以完成更加丰富的特征表达和运算。

虽然FFN的输入输出维度都是512，但是输出的512维度特征和输入的512为特征是不一样的。输出的512维度特征是在隐层空间（2048）的基础上进一步融合得到的。可以说，输出的512维比输入的512维具有更加丰富和准确的特征表示。