平面三连杆机械臂ik(SO-ARM100可用此简化逆解控制)

原创已于 2025-06-27 17:25:09 修改 · 391 阅读

·

4

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#平面 #机器人

于 2025-06-05 14:56:07 首次发布

常规三连杆

$x_e = l_1\cos \theta_1+l_2\cos( \theta_1+\theta_2)+l_3\cos ( \theta_1+\theta_2+\theta_3)$

$y_e = l_1\sin \theta_1+l_2\sin ( \theta_1+\theta_2)+l_3\sin ( \theta_1+\theta_2+\theta_3)$

$\phi_e = \theta_1+\theta_2+\theta_3$

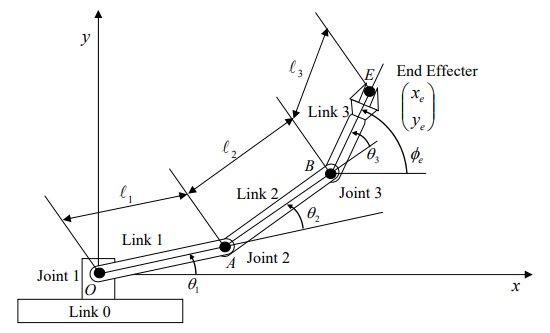
上述公式实现正解（Forward Kinematic）

为解决其逆运动学问题，运动学结构重绘于下图。问题在于找到三个关节角度θ1、θ2、θ3，使末端执行器到达期望位置和姿态(xe,ye,ϕe)。我们采用两步法：首先，根据(xe,ye,ϕe)求解腕部位置（点B）；然后，根据腕部位置求解θ1、θ2；角度θ3可直接由腕部位置确定

$x_w = x_e-l_3\cos\phi_e$

$y_w = y_e-l_3\sin\phi_e$

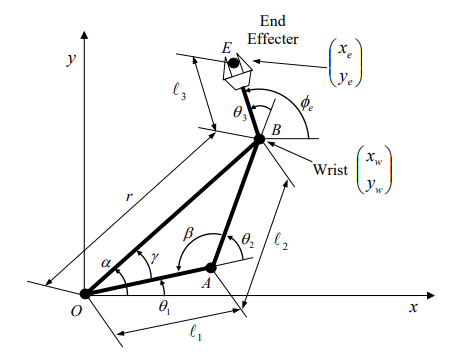
接着

$\alpha = \tan^{-1}\frac{y_w}{x_w}$

根据余弦定理可得：

$l^2_1+l^2_2-2l_1l_2\cos\beta = r^2$

$\theta_2 = 180^{\circ}-\beta = \pi-\cos^{-1}\frac{l^2_1+l^2_2-x^2_w-y^2_w}{2l_1l_2}$

$\theta_1 = \alpha-\gamma = tan^{-1}\frac{y_w}{x_w}-cos^{-1}\frac{l^2_1-l^2_2+x^2_w+y^2_w}{2l_1\sqrt{x^2_w+y^2_w}}$

$\theta_3 = \phi_e-\theta_1-\theta_2$

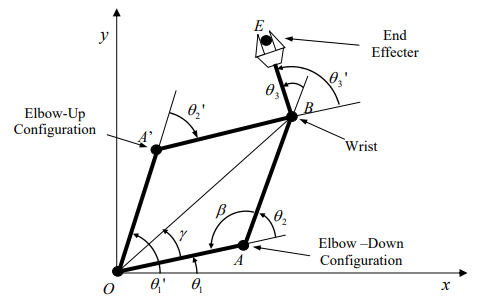
而另一个解可得：

$\theta'_1 =\alpha+\gamma$

$\theta'_2 =-\theta_2$

$\theta'_3 = \phi_e-\theta_1'-\theta_2'$

SO-ARM100（微变化的三连杆）

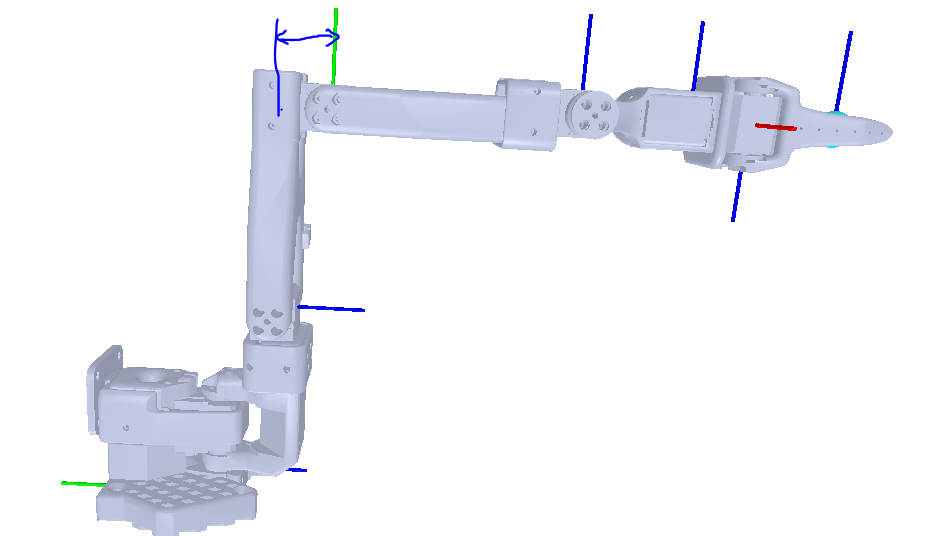
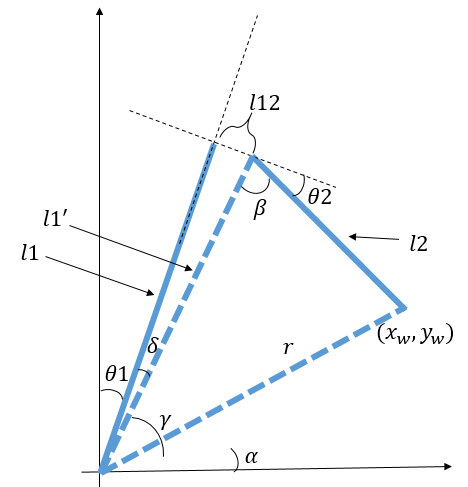
此机械臂在第二第三关节中间有一段固定偏移。下述定义的关节角与上方不一致，这个定义直接符合上述机械臂里的角度定义，无需额外转换。

$l'_1= \sqrt{l_1^2+l_{12}^2}$

$\theta_2 = 90^{\circ}-\delta+\beta = \pi/2+\tan^{-1}\frac{l_{12}}{l_1}-\cos^{-1}\frac{l'^2_1+l^2_2-x^2_w-y^2_w}{2l'_1l_2}$

$\theta_1 = 90-\alpha-\gamma-\delta$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。