pytorch搭建WGAN

最新推荐文章于 2025-06-02 09:04:10 发布

弱小的皮卡龙

最新推荐文章于 2025-06-02 09:04:10 发布

阅读量1.1k

点赞数

CC 4.0 BY-SA版权

分类专栏： Gans 文章标签： pytorch WGAN Wasserstein

本文链接：https://blog.youkuaiyun.com/tgj2094942564/article/details/119990494

DCGAN只是在网络结构上做了相应的改进，但是实质上并没有解决gan中的本质缺陷
Wasserstein GAN（下面简称WGAN）成功地做到了以下爆炸性的几点：

彻底解决GAN训练不稳定的问题，不再需要小心平衡生成器和判别器的训练程度
基本解决了collapse mode的问题，确保了生成样本的多样性
训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程，这个数值越小代表GAN训练- 得越好，代表生成器产生的图像质量越高

该论文的公式较多，本文只做简单的描述即可

原始GAN中判别器要最小化如下损失函数，尽可能把真实样本分为正例，生成样本分为负例

根据原始GAN定义的判别器loss，我们可以得到最优判别器的形式；而在最优判别器的下，我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布与生成分布[公之间的JS散度。我们越训练判别器，它就越接近最优，最小化生成器的loss也就会越近似于最小化和之间的JS散度。

问题就出在这个JS散度上。我们会希望如果两个分布之间越接近它们的JS散度越小，但是JS散度的问题在于，当两个分布没有接触时或者接触可以忽略，JS值会固定为log2，导致梯度消失

而Wesserstein GAN提出了新的解决方案，引入了Wesserstein 距离，表示将生成分布 “搬” 运成真实分布的最小“开销”
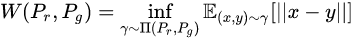
在这里插入图片描述

Wasserstein距离相比KL散度、JS散度的优越性在于，即便两个分布没有重叠，Wasserstein距离仍然能够反映它们的远近

最后得到判别器的损失函数为：
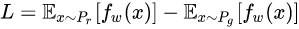
在这里插入图片描述
尽可能取到最大，此时就会近似真实分布与生成分布之间的Wasserstein距离（忽略常数倍数[公式]）。注意原始GAN的判别器做的是真假二分类任务，所以最后一层是sigmoid，但是现在WGAN中的判别器做的是近似拟合Wasserstein距离，属于回归任务，所以要把最后一层的sigmoid拿掉。

生成器的损失函数为：
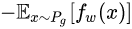
在这里插入图片描述
公式15是公式17的反，可以指示训练进程，其数值越小，表示真实分布与生成分布的Wasserstein距离越小，GAN训练得越好。

import torch
import torch.nn as nn

import torch.optim as optim
import torchvision
import torchvision.datasets as datasets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter

class Discriminator(nn.Module):
    def __init__(self, channels_img, features_d):
        super(Discriminator, self).__init__()
        self.disc = nn.Sequential(
            # input: N x channels_img x 64 x 64
            nn.Conv2d(
                channels_img, features_d, kernel_size=4, stride=2, padding=1
            ),
            nn.LeakyReLU(0.2),
            # _block(in_channels, out_channels, kernel_size, stride, padding)
            self._block(features_d, features_d * 2, 4, 2, 1),
            self._block(features_d * 2, features_d * 4, 4, 2, 1),
            self._block(features_d * 4, features_d * 8, 4, 2, 1),
            # After all _block img output is 4x4 (Conv2d below makes into 1x1)
            nn.Conv2d(features_d * 8, 1, kernel_size=4, stride=2, padding=0),
        )

    def _block(self, in_channels, out_channels, kernel_size, stride, padding):
        return nn.Sequential(
            nn.Conv2d(
                in_channels