Norm,也即 Normalization,已经是深度神经网络模型中非常常规的操作了,但它背后的实现,原理和作用等,其实我们可以理解的更细致,本文会以最常用的 BatchNorm 和 LayerNorm 为例(其他 Norm 方法大同小异),通过 Q&A 的形式,去深入理解关于 Norm 的细节知识点。
BN 在训练和测试时的差异
BN 中的移动平均 Moving Average 是怎么做的?
移动平均中 Momentum 参数的影响
Norm 中的标准化、平移和缩放的作用
不同 Norm 方法中都有哪些参数要保存?
BN 和 LN 有哪些差异?
为什么 BERT 使用 LN,而不使用 BN?
如何去理解在哪一个维度做 Norm?
所有文字不如代码准确,决定先上一个简化版的MyBN1d和MyLN镇楼:
MyBN1d:
import torch.nn as nn
import torch
class MyBN1d(nn.Module):
def __init__(self, momentum=0.1, eps=1e-5, feat_dim=2):
super(MyBN1d, self).__init__()
# 更新self._running_xxx时的动量
self._momentum = momentum
# 防止分母计算为0
self._eps = eps
# running_mean和running_var都是要存在模型weights里,但是不需要更新参数,所以self.register_buffer
self.register_buffer('_running_mean', torch.zeros(1,feat_dim,1))
self.register_buffer('_running_var', torch.ones(1,feat_dim,1))
# weight和bias都是需要训练时候更新参数的
self._weight = nn.Parameter(torch.ones(1,feat_dim,1))
self._bias = nn.Parameter(torch.zeros(1,feat_dim,1))
def forward(self, x):
if self.training: #self.training是nn.Module自带参数,net.train()和net.eval()会改变这个值
# x_mean = x.mean([0,2])
# x_var = x.var([0,2], correction=0) #correction=0表示分母是不是归一化
x_mean = x.mean(dim=(0,2), keepdims=True)
x_var = x.var(dim=(0,2), keepdims=True, correction=0)
# 对应running_mean的更新公式,下面注释是备用写法
# self._running_mean = (1-self._momentum)*self._running_mean + self._momentum*x_mean
# self._running_var = (1-self._momentum)*self._running_var + self._momentum*x_var
self._running_mean -= self._momentum*(x_mean-self._running_mean)
self._running_var -= self._momentum * (x_mean - self._running_var)
# [None,:,None]不常看有点恶心,相当于x_mean.unsqueeze(0).unsqueeze(2),也就是把一个shape是(feat_dim)的Tensor变成了(1,feat_dim,1),以下是备用写法
# x_hat = (x-x_mean[None,:,None])/torch.sqrt(x_var[None,:,None]+self._eps)
x_hat = (x-x_mean)/torch.sqrt(x_var+self._eps)
else:
# 注意上面训练的时候不要用running_mean做差输出
# x_hat = (x-self._running_mean[None,:,None])/torch.sqrt(self._running_var[None,:,None]+self._eps)
x_hat = (x-self._running_mean)/torch.sqrt(self._running_var+self._eps)
return self._weight*x_hat + self._bias
#CV中的feat_num, num_features, hidden_size都是指中间那个维度
feat_dim=3
x = torch.randn(2,feat_dim,5)
bn1d = nn.BatchNorm1d(feat_dim)
out_bn1d = bn1d(x)
print(out_bn1d)
mybn1d = MyBN1d(feat_dim=feat_dim)
out_mybn1d = mybn1d(x)
print(out_mybn1d)
'''
两个输出都是一样的:
tensor([[[-0.9176, 1.4579, 0.2473, 0.7218, 1.0444],
[-0.7802, 0.3168, 0.8793, -0.4985, 2.3281],
[ 1.6315, 0.4317, 0.1170, -0.3623, -1.5179]],
[[ 0.8724, 0.0181, -0.9045, -0.7437, -1.7963],
[ 0.0180, -0.1456, -0.6095, -1.5661, 0.0578],
[-1.6694, 0.4632, -0.6507, 0.9601, 0.5968]]],
grad_fn=<NativeBatchNormBackward0>)
tensor([[[-0.9176, 1.4579, 0.2473, 0.7218, 1.0444],
[-0.7802, 0.3168, 0.8793, -0.4985, 2.3281],
[ 1.6315, 0.4317, 0.1170, -0.3623, -1.5179]],
[[ 0.8724, 0.0181, -0.9045, -0.7437, -1.7963],
[ 0.0180, -0.1456, -0.6095, -1.5661, 0.0578],
[-1.6694, 0.4632, -0.6507, 0.9601, 0.5968]]],
grad_fn=<AddBackward0>)
'''
MyLN:
import torch
from torch import nn
class MyLN(nn.Module):
def __init__(self, normalized_shape, # 在哪个维度上做LN
eps: float = 1e-5, # 防止分母为0
elementwise_affine: bool = True): # 是否使用可学习的缩放因子和偏移因子
super(MyLN, self).__init__()
# 需要对哪个维度的特征做LN, torch.size查看维度
self.normalized_shape = normalized_shape # [c,w*h]
self.eps = eps
self.elementwise_affine = elementwise_affine
# 构造可训练的缩放因子和偏置
if self.elementwise_affine:
self.weight = nn.Parameter(torch.ones(normalized_shape)) # [c,w*h]
self.bias = nn.Parameter(torch.zeros(normalized_shape)) # [c,w*h]
def forward(self, x: torch.Tensor): # [b,c,w*h]
# 需要做LN的维度和输入特征图对应维度的shape相同
assert self.normalized_shape == x.shape[-len(self.normalized_shape):] # [-2:]
# 需要做LN的维度索引
dims = [-(i + 1) for i in range(len(self.normalized_shape))] # [b,c,w*h]维度上取[-1,-2]维度,即[c,w*h]
# 计算特征图对应维度的均值和方差
mean = x.mean(dim=dims, keepdims=True) # [b,1,1]
mean_x2 = (x ** 2).mean(dim=dims, keepdims=True) # [b,1,1]
var = mean_x2 - mean ** 2 # [b,c,1,1]
x_norm = (x - mean) / torch.sqrt(var + self.eps) # [b,c,w*h]
# 线性变换
if self.elementwise_affine:
x_norm = self.weight * x_norm + self.bias # [b,c,w*h]
return x_norm
if __name__ == '__main__':
x = torch.randn(2,3,5)
my_ln = MyLN(x.shape[1:])
print(my_ln(x))
ln = nn.LayerNorm(x.shape[1:])
print(ln(x))
'''
两个输出都是一样的:
tensor([[[-0.4581, 1.5668, 0.6686, -0.4423, -0.7992],
[ 0.1808, 0.7245, 0.3380, -1.1207, 1.3641],
[ 0.4380, -2.3911, -0.1461, -0.7776, 0.8543]],
[[ 1.3458, 0.4072, -2.2993, -0.7033, -0.7776],
[ 0.3645, 0.2430, 0.0801, 0.5956, 0.5822],
[ 0.1153, 0.9114, -0.0091, 1.0779, -1.9336]]],
grad_fn=<AddBackward0>)
tensor([[[-0.4581, 1.5668, 0.6686, -0.4423, -0.7992],
[ 0.1808, 0.7245, 0.3380, -1.1207, 1.3641],
[ 0.4380, -2.3911, -0.1461, -0.7776, 0.8543]],
[[ 1.3458, 0.4072, -2.2993, -0.7033, -0.7776],
[ 0.3645, 0.2430, 0.0801, 0.5956, 0.5822],
[ 0.1153, 0.9114, -0.0091, 1.0779, -1.9336]]],
grad_fn=<NativeLayerNormBackward0>)
'''关于weight和bias的shape一些思考,所以就是BN的shape就是(1,feat_num,1),LN的shape就是normlized_shape,就是要把最后几维给对齐了:
'''
import torch
a = torch.arange(30).reshape(2,3,5)
b = torch.arange(3) #这样广播是不work的
c = a*b
print(c.shape)
'''
'''
import torch
a = torch.arange(30).reshape(2,3,5)
b = torch.arange(5) #这样广播work
c = a*b
print(c.shape)
'''
import torch
a = torch.arange(30).reshape(2,3,5)
b = torch.arange(3).reshape(3,1) #这样广播也work
c = a*b
print(c.shape)

BN在训练和测试时的差异
对于 BN,在训练时,是对每一个 batch 的训练数据进行归一化,也即用每一批数据的均值和方差。
而在测试时,比如进行一个样本的预测,就并没有 batch 的概念,因此,这个时候用的均值和方差是在训练过程中通过滑动平均得到的均值和方差,这个会和模型权重一起,在训练完成后一并保存下来。
对于 BN,是对每一批数据进行归一化到一个相同的分布,而每一批数据的均值和方差会有一定的差别,而不是用固定的值,这个差别实际上也能够增加模型的鲁棒性,并会在一定程度上减少过拟合。
但是一批数据和全量数据的均值和方差相差太多,又无法较好地代表训练集的分布,因此,BN 一般要求将训练集完全打乱,并用一个较大的 batch 值,去缩小与全量数据的差别。
卷积层使用 Batch Normalization#
卷积层, 例如对于图像的卷积的时候, 我们往往不会考虑每一个像素, 注意, 实际上, 往往每一个像素是作为一个特征, 并且还有其 𝑅𝐺𝐵 值, 这样特征就更多了, 但是, 我们考虑对于图像来说, 不同位置的像素特征本质上属性是相同的, 这里参考 Feature Map(特征图), 我们将一个特征图内的所有特征做相同的归一化, 也就是说, 上述的 𝛾 与 𝛽 函数对于每个 Feature Map是相同的, 对不同的Feature Map 是不同的, 个人觉得 Feature Map的大小和CNN 的channels 大小相同, 或者说是 channels 的另一种说法. 我们可以从下面的例子看出他们之间的关系.
import torch
from torch import nn
# 随机生成一个Batch的模拟,100张16通道784像素点的数据
# 均匀分布U(0~1)
x = torch.rand(100, 16, 784)
# Batch Normalization层,因为输入是将高度H和宽度W合成了一个维度,所以这里用1d
layer = nn.BatchNorm1d(16) # 传入通道数, 本质就是 Feature Map的大小, 在100*784个数上算均值方差,得到长度为16的均值方差,这个16刚好就是running_mean,running_var的形状
# 随着 CNN 层数的前进, 这里变成上一层 CNN 中核的个数
out = layer(x)
x = torch.randn(1, 16, 7, 7) # 1张16通道的7乘7的图像
# Batch Normalization层,因为输入是有高度H和宽度W的,所以这里用2d
layer = nn.BatchNorm2d(16) # 传入通道数
out = layer(x)class _NormBase(Module):
"""Common base of _InstanceNorm and _BatchNorm"""
_version = 2
__constants__ = ["track_running_stats", "momentum", "eps", "num_features", "affine"]
num_features: int
eps: float
momentum: float
affine: bool
track_running_stats: bool
# WARNING: weight and bias purposely not defined here.
# See https://github.com/pytorch/pytorch/issues/39670
def __init__(
self,
num_features: int,
eps: float = 1e-5,
momentum: float = 0.1,
affine: bool = True,
track_running_stats: bool = True,
device=None,
dtype=None
) -> None:
factory_kwargs = {'device': device, 'dtype': dtype}
super(_NormBase, self).__init__()
self.num_features = num_features
self.eps = eps
self.momentum = momentum
self.affine = affine
self.track_running_stats = track_running_stats
if self.affine:
self.weight = Parameter(torch.empty(num_features, **factory_kwargs))
self.bias = Parameter(torch.empty(num_features, **factory_kwargs))
else:
self.register_parameter("weight", None)
self.register_parameter("bias", None)
if self.track_running_stats:
self.register_buffer('running_mean', torch.zeros(num_features, **factory_kwargs))
self.register_buffer('running_var', torch.ones(num_features, **factory_kwargs))
self.running_mean: Optional[Tensor]
self.running_var: Optional[Tensor]
self.register_buffer('num_batches_tracked',
torch.tensor(0, dtype=torch.long,
**{k: v for k, v in factory_kwargs.items() if k != 'dtype'}))
else:
self.register_buffer("running_mean", None)
self.register_buffer("running_var", None)
self.register_buffer("num_batches_tracked", None)
self.reset_parameters() 
def reset_running_stats(self) -> None:
# 将预测过程中的 running_mean 和 running_var 初始化为标注正态分布
if self.track_running_stats:
# running_mean/running_var/num_batches... are registered at runtime depending
# if self.track_running_stats is on
self.running_mean.zero_() # type: ignore[union-attr]
self.running_var.fill_(1) # type: ignore[union-attr]
self.num_batches_tracked.zero_() # type: ignore[union-attr,operator] 

def forward(self, input: Tensor) -> Tensor:
self._check_input_dim(input)
# exponential_average_factor is set to self.momentum
# (when it is available) only so that it gets updated
# in ONNX graph when this node is exported to ONNX. 滑动平均系数,
if self.momentum is None:
exponential_average_factor = 0.0
else:
exponential_average_factor = self.momentum
if self.training and self.track_running_stats:
# TODO: if statement only here to tell the jit to skip emitting this when it is None
if self.num_batches_tracked is not None: # type: ignore[has-type]
# 记录 batch 的个数, 也就是 running mean 的个数
self.num_batches_tracked = self.num_batches_tracked + 1 # type: ignore[has-type]
# 使用累计滑动平均, 或者指数滑动平均
if self.momentum is None: # use cumulative moving average
exponential_average_factor = 1.0 / float(self.num_batches_tracked)
else: # use exponential moving average
exponential_average_factor = self.momentum
r"""
Decide whether the mini-batch stats should be used for normalization rather than the buffers.
Mini-batch stats are used in training mode, and in eval mode when buffers are None.
"""
# 这里主要是判断 evaluation 阶段是否使用 mini-batch 计算得到的running mean 与 running variance
if self.training:
bn_training = True
else:
bn_training = (self.running_mean is None) and (self.running_var is None)
r"""
Buffers are only updated if they are to be tracked and we are in training mode. Thus they only need to be passed when the update should occur (i.e. in training mode when they are tracked), or when buffer stats are used for normalization (i.e. in eval mode when buffers are not None).
"""
return F.batch_norm(
input,
# If buffers are not to be tracked, ensure that they won't be updated
self.running_mean
if not self.training or self.track_running_stats
else None,
self.running_var if not self.training or self.track_running_stats else None,
self.weight,
self.bias,
bn_training,
exponential_average_factor,
self.eps,
)
BN中的移动平均Moving Average是怎么做的?
训练过程中的每一个 batch 都会进行移动平均的计算 [1] :
moving_mean = moving_mean * momentum + batch_mean * (1 - momentum)
moving_var = moving_var * momentum + batch_var * (1 - momentum)式中的 momentum 为动量参数,在 TF/Keras 中,该值为 0.99,在 Pytorch 中,这个值为 0.9 初始值,moving_mean=0,moving_var=1,相当于标准正态分布。
在实际的代码中,滑动平均的计算会以下面这种更高效的方式,但实际上是等价的:
moving_mean -= (moving_mean - batch_mean) * (1 - momentum)
moving_var -= (moving_var - batch_var) * (1 - momentum)

移动平均中Momentum参数的影响
整个训练阶段滑动平均的过程,(moving_mean, moving_var)参数实际上是从正态分布,向训练集真实分布靠拢的一个过程。
理论上,训练步数越长是会越靠近真实分布的,实际上,因为每个 batch 并不能代表整个训练集的分布,所以最后的值是在真实分布附近波动。
一个更小的 momentum 值,意味着更大的更新步长,对应着滑动平均值更快的变化,能更快地向真实值靠拢,但也意味着更大的波动性,更大的 momentum 值则相反。
训练阶段使用的是(batch_mean, batch_var),所以滑动平均并不会影响训练阶段的结果,而是影响预测阶段的效果 。
如果训练步数很短,一个大的 momentum 值可能会导致(moving_mean, moving_var)还没有靠拢到真实分布就停止了,这样对预测阶段的影响是很大的,也会是欠拟合的一个状态。如果训练步数足够,一个大的 momentum 值对应小的更新步长,最后的滑动平均的值是会更接近真实值的。
如果 batch size 比较小,那单个 batch 的(batch_mean, batch_var)和真实分布会比较大,此时滑动平均单次更新的步长就不应过大,适用一个大的 momentum 值,反之可类比分析。

Norm中的标准化、平移和缩放的作用
对于一般的神经网络,它有这样一些问题 [2] :
其一,上层参数需要不断适应新的输入数据分布,降低学习速度。
其二,下层输入的变化可能趋向于变大或者变小,导致上层落入饱和区,使得学习过早停止。
其三,每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能的谨慎。
Norm 的使用,可以很好的改善这些问题,它包括两个操作:标准化 + 平移和缩放(注:本文中所有的 Norm 也都代指这两个操作)。
首先,抛开神经网络的背景,标准化这个操作,可以消除不同数据之间由于量纲/数量级带来的差异,而且它是一种线性变换,并不会改变原始数据的数值排序关系。
经过标准化,每层神经网络的输出变成了均值为 0,方差为 1 的标准分布,不再受到下层神经网络的影响(注意是数据分布不受影响,但具体的值肯定还是依赖下层神经网络的输出),可以有效改善上述的几个问题。
那平移和缩放的作用在哪里呢?主要还是为了:保证模型的表达能力不因为标准化而下降。
在 Norm 中引入的两个新参数 γ 和 β,可以表示旧参数作为输入的同一族函数,但是新参数有不同的学习动态。在旧参数中,x 的均值和方差取决于下层神经网络的复杂关联;但在新参数中,x 的均值和方差仅由 γ 和 β 来确定,去除了与下层计算的密切耦合。新参数很容易通过梯度下降来学习,简化了神经网络的训练。
如果直接只做标准化不做其他处理,神经网络是学不到任何东西的,因为标准化之后都是标准分布了,但是加入这两个参数后就不一样了。
先考虑特殊情况,如果 γ 和 β 分别等于此 batch 的标准差和均值,那么 y 不就还原到标准化前的 x 了吗,也即是缩放平移到了标准化前的分布,相当于 Norm 没有起作用。这样就保证了每一次数据经过 Norm 后还能保留学习来的特征,同时又能完成标准化这个操作,从而使当前神经元的分布摆脱了对下层神经元的依赖。
注:该问题主要参考 [2],讲解非常清晰和系统,非常值得一看。
------------
我们可以看到,第一步的变换将输入数据限制到了一个全局统一的确定范围(均值为 0、方差为 1)。下层神经元可能很努力地在学习,但不论其如何变化,其输出的结果在交给上层神经元进行处理之前,将被粗暴地重新调整到这一固定范围。
沮不沮丧?沮不沮丧?
难道我们底层神经元人民就在做无用功吗?
所以,为了尊重底层神经网络的学习结果,我们将规范化后的数据进行再平移和再缩放,使得每个神经元对应的输入范围是针对该神经元量身定制的一个确定范围(均值为 β 、方差为γ ^2 )。rescale 和 reshift 的参数都是可学习的,这就使得 Normalization 层可以学习如何去尊重底层的学习结果。
除了充分利用底层学习的能力,另一方面的重要意义在于保证获得非线性的表达能力。Sigmoid 等激活函数在神经网络中有着重要作用,通过区分饱和区和非饱和区,使得神经网络的数据变换具有了非线性计算能力。而第一步的规范化会将几乎所有数据映射到激活函数的非饱和区(线性区),仅利用到了线性变化能力,从而降低了神经网络的表达能力。而进行再变换,则可以将数据从线性区变换到非线性区,恢复模型的表达能力。
------------

不同Norm方法中都有哪些参数要保存?
BN 的参数包括:
1)每个神经元在训练过程中得到的均值和方差,通过移动平均得到,在pytorch中是track_running_stats这个参数
2)每个神经元上的缩放参数 γ 和平移参数 β,分别对应weights和bias,在pytorch中是affine这个参数
LN 只包括上面的第 2 部分参数,因为它和 batch 无关,无需记录第 1 部分参数。

BN和LN有哪些差异?
下图蓝色是BN,黄色是LN

1)两者做 Norm 的维度不一样,BN 是在 Batch 维,而 LN 一般是在最后一维。
2)BN 需要在训练过程中,滑动平均累积每个神经元的均值和方差,并保存在模型文件中用于推理过程,而 LN 不需要。
3)因为 Norm 维度的差异,使得它们适用的领域也有差异,BN 更多用于 CV 领域,LN 更多用于 NLP 领域。

为什么Transformer/BERT使用LN,而不使用BN?
最直白的原因,还是因为用 LN 的效果更好,这个在 Transformer 论文中作者有说到。但背后更深层次的原因,这个在知乎上有广泛的讨论 [3],不过并没有一个统一的结论,这里我摘录两个我相对认可的回答 [4][5] :
图像数据是自然界客观存在的,像素的组织形式已经包含了“信息”,而 NLP 数据不一样,网络对 NLP 数据学习的真正开端是从'embedding'开始的,而这个'embedding'并不是客观存在,它也是通过网络学习出来的。
下面只从直观理解上从两个方面说说个人看法:
1. layer normalization 有助于得到一个球体空间中符合 0 均值 1 方差高斯分布的 embedding,batch normalization不具备这个功能;
2. layer normalization 可以对 transformer 学习过程中由于多词条 embedding 累加可能带来的“尺度”问题施加约束,相当于对表达每个词一词多义的空间施加了约束,有效降低模型方差。batch normalization 也不具备这个功能。
emmbedding 并不存在一个客观的分布,那我们需要考虑的是:我们希望得到一个符合什么样分布的 embedding?
很好理解,通过 layer normalization 得到的 embedding 是以坐标原点为中心,1 为标准差,越往外越稀疏的球体空间中。
说简单点,其实深度学习里的正则化方法就是“通过把一部分不重要的复杂信息损失掉,以此来降低拟合难度以及过拟合的风险,从而加速了模型的收敛”。Normalization 目的就是让分布稳定下来(降低各维度数据的方差)。
不同正则化方法的区别只是操作的信息维度不同,即选择损失信息的维度不同。
在 CV 中常常使用 BN,它是在 NHW 维度进行了归一化,而 Channel 维度的信息原封不动,因为可以认为在 CV 应用场景中,数据在不同 channel 中的信息很重要,如果对其进行归一化将会损失不同 channel 的差异信息。
而 NLP 中不同 batch 样本的信息关联性不大,而且由于不同的句子长度不同,强行归一化会损失不同样本间的差异信息,所以就没在 batch 维度进行归一化,而是选择 LN,只考虑的句子内部维度的归一化。可以认为 NLP 应用场景中一个样本内部维度间是有关联的,所以在信息归一化时,对样本内部差异信息进行一些损失,反而能降低方差。
总结一下:选择什么样的归一化方式,取决于你关注数据的哪部分信息。如果某个维度信息的差异性很重要,需要被拟合,那就别在那个维度进行归一化。

如何去理解在哪一个维度做Norm?
以 BERT 每一层 bert_tensor 的维度:[batch_size, seq_len, hidden_size] 为例,直接说「BatchNorm就对应dim=0,LayerNorm就对应dim=-1」这样歧义比较大。准确一点来说:
- BatchNorm是每次拿着dim=0和dim=1的batch_size*seq_len个数算均值方差,这batch_size*seq_len个数组成的平面要垂直于边hidden_size;如果换成CV的输入[bs,c,w*h],那么就是dim=0和dim=2的bs*w*h个数算均值方法,可以直接用pytorch里x.mean(dim=(0,2),keepdims=True)这个方法
- LayerNorm在normalize_shape=(hidden_size)是每次拿着dim=-1的hidden_size个数算均值方差(叫做Norm也行),这hidden_size个数滑动组成的平面要垂直于边batch_size,Transformer中用的是这一种
- LayerNorm在normalize_shape=(seq_len,hidden_size)是每次拿着seq_len*hidden_size个数算均值方差(叫做Norm也行),这seq_len*hidden_size个数组成的平面要垂直于边batch_size
如果用下面这个图来看,[batch_size, seq_len, hidden_size]=[N,H*W,C]。图片里的C是channel个数,或者叫feature_nums,放在文本里就是hidden_size;图片里的H*W是一张图的像素个数,放在文本里就是seq_len,一句话有几个词;图片和文本里的batch_size分别表示有几张图和几句话
BN和LN在pytorch里的实现接口是不相同的:BN初始化时传入的是feature_nums;到了LN初始化时传入的却是normalized_shape,个人理解这么设计原因是normalized_shape有时候可以倒着数传个多维的进去,BN八成是没这个场景;本质上说feature_num和normalized_shape其实都是normalized_shape,只不过没有见过BN里normalized_shape退化成一维IN的场景

BN 是在 batch_size*hidden_size 平面做 Norm(算均值方差),则:
for j in range(hidden_size):
Norm([[bert_tensor[k][i][j] for i in range(seq_len)] for k in range(batch_size)])LN是在 hidden_size 维做 Norm(算均值方差),这是典型Transformer场景,则:
for i in range(batch_size):
for j in range(seq_len):
Norm([bert_tensor[i][j][k] for k in range(hidden_size)])
LN其实也可以拿个hidden_size*seq_len个数一起算均值方差。。。
也就是说,对哪个维度做 Norm,就在其他维度不动的情况下,基于该维度下的所有元素计算均值和方差,然后再做 Norm。
LayerNorm在transformer里是作用在embedding_dim那个维度上的。但是torch.LayerNorm不像softmax的实现指定dim,而是指定了dim的倒数的shape,容易晕,贴个code清醒一下:
import torch
from torch import nn
def layer_norm_process(input: torch.tensor, normalize_shape, eps=1e-5):
# pytorch实现中还有elementwise_affine,为true的情况下用来学习weight和bias
normalize_shape_len = len(normalize_shape)
# layernorm传入的是倒数几维要Normalize的shape
assert input.size()[-normalize_shape_len:] == normalize_shape
# 如果normalized_shape是3,那么torch.var_mean的dim就是-1
var_mean = torch.var_mean(input, dim=tuple([i for i in range(-normalize_shape_len, 0, 1)]), unbiased=False)
# 不带unbiase=False结果会有所不同
var, mean = var_mean[0], var_mean[1]
res = (input - mean[(...,) + (None,) * normalize_shape_len]) / torch.sqrt(
var[(...,) + (None,) * normalize_shape_len] + eps)
return res
def batch_norm_process(input: torch.tensor, eps=1e-5):
var_mean = torch.var_mean(input, dim=(0,2), unbiased=False)
# 不带unbiase=False结果会有所不同
var, mean = var_mean[0], var_mean[1]
#None的位置相当于unsqueeze(dim)
res = (input - mean[None,:,None]) / torch.sqrt(var[None,:,None] + eps)
return res
def batch_norm_process_2d(input: torch.tensor, eps=1e-5):
var_mean = torch.var_mean(input, dim=(0,2,3), unbiased=False)
# 不带unbiase=False结果会有所不同
var, mean = var_mean[0], var_mean[1]
res = (input - mean[None,:,None,None]) / torch.sqrt(var[None,:,None,None] + eps)
return res
x = torch.arange(24).float().reshape(2,3,4)
bn1d = nn.BatchNorm1d(3, track_running_stats=False, affine=False)
ln = nn.LayerNorm(4)
print('x={}'.format(x))
print('bn1d={}'.format(bn1d(x)))
print('my_bn={}'.format(batch_norm_process(x, eps=1e-5)))
print('ln={}'.format(ln(x)))
print('my_ln={}'.format(layer_norm_process(x, (4,), eps=1e-5)))
'''
输出如下:
x=tensor([[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]],
[[12., 13., 14., 15.],
[16., 17., 18., 19.],
[20., 21., 22., 23.]]])
bn1d=tensor([[[-1.2288, -1.0650, -0.9012, -0.7373],
[-1.2288, -1.0650, -0.9012, -0.7373],
[-1.2288, -1.0650, -0.9012, -0.7373]],
[[ 0.7373, 0.9012, 1.0650, 1.2288],
[ 0.7373, 0.9012, 1.0650, 1.2288],
[ 0.7373, 0.9012, 1.0650, 1.2288]]])
my_bn=tensor([[[-1.2288, -1.0650, -0.9012, -0.7373],
[-1.2288, -1.0650, -0.9012, -0.7373],
[-1.2288, -1.0650, -0.9012, -0.7373]],
[[ 0.7373, 0.9012, 1.0650, 1.2288],
[ 0.7373, 0.9012, 1.0650, 1.2288],
[ 0.7373, 0.9012, 1.0650, 1.2288]]])
ln=tensor([[[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416]],
[[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416]]],
grad_fn=<NativeLayerNormBackward0>)
my_ln=tensor([[[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416]],
[[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416],
[-1.3416, -0.4472, 0.4472, 1.3416]]])
'''
x2 = torch.arange(24*4).float().reshape(2,3,4,4)
bn2d = nn.BatchNorm2d(3, track_running_stats=False, affine=False)
print('bn2d={}'.format(bn2d(x2)))
print('my_bn={}'.format(batch_norm_process_2d(x2, eps=1e-5)))
'''
输出为:
bn2d=tensor([[[[-1.2889, -1.2480, -1.2071, -1.1662],
[-1.1253, -1.0843, -1.0434, -1.0025],
[-0.9616, -0.9207, -0.8798, -0.8388],
[-0.7979, -0.7570, -0.7161, -0.6752]],
[[-1.2889, -1.2480, -1.2071, -1.1662],
[-1.1253, -1.0843, -1.0434, -1.0025],
[-0.9616, -0.9207, -0.8798, -0.8388],
[-0.7979, -0.7570, -0.7161, -0.6752]],
[[-1.2889, -1.2480, -1.2071, -1.1662],
[-1.1253, -1.0843, -1.0434, -1.0025],
[-0.9616, -0.9207, -0.8798, -0.8388],
[-0.7979, -0.7570, -0.7161, -0.6752]]],
[[[ 0.6752, 0.7161, 0.7570, 0.7979],
[ 0.8388, 0.8798, 0.9207, 0.9616],
[ 1.0025, 1.0434, 1.0843, 1.1253],
[ 1.1662, 1.2071, 1.2480, 1.2889]],
[[ 0.6752, 0.7161, 0.7570, 0.7979],
[ 0.8388, 0.8798, 0.9207, 0.9616],
[ 1.0025, 1.0434, 1.0843, 1.1253],
[ 1.1662, 1.2071, 1.2480, 1.2889]],
[[ 0.6752, 0.7161, 0.7570, 0.7979],
[ 0.8388, 0.8798, 0.9207, 0.9616],
[ 1.0025, 1.0434, 1.0843, 1.1253],
[ 1.1662, 1.2071, 1.2480, 1.2889]]]])
my_bn=tensor([[[[-1.2889, -1.2480, -1.2071, -1.1662],
[-1.1253, -1.0843, -1.0434, -1.0025],
[-0.9616, -0.9207, -0.8798, -0.8388],
[-0.7979, -0.7570, -0.7161, -0.6752]],
[[-1.2889, -1.2480, -1.2071, -1.1662],
[-1.1253, -1.0843, -1.0434, -1.0025],
[-0.9616, -0.9207, -0.8798, -0.8388],
[-0.7979, -0.7570, -0.7161, -0.6752]],
[[-1.2889, -1.2480, -1.2071, -1.1662],
[-1.1253, -1.0843, -1.0434, -1.0025],
[-0.9616, -0.9207, -0.8798, -0.8388],
[-0.7979, -0.7570, -0.7161, -0.6752]]],
[[[ 0.6752, 0.7161, 0.7570, 0.7979],
[ 0.8388, 0.8798, 0.9207, 0.9616],
[ 1.0025, 1.0434, 1.0843, 1.1253],
[ 1.1662, 1.2071, 1.2480, 1.2889]],
[[ 0.6752, 0.7161, 0.7570, 0.7979],
[ 0.8388, 0.8798, 0.9207, 0.9616],
[ 1.0025, 1.0434, 1.0843, 1.1253],
[ 1.1662, 1.2071, 1.2480, 1.2889]],
[[ 0.6752, 0.7161, 0.7570, 0.7979],
[ 0.8388, 0.8798, 0.9207, 0.9616],
[ 1.0025, 1.0434, 1.0843, 1.1253],
[ 1.1662, 1.2071, 1.2480, 1.2889]]]])
'''不管BN还是LN输入输出的shape都不会发生变化
转载自: 超细节的BatchNorm/BN/LayerNorm/LN知识点

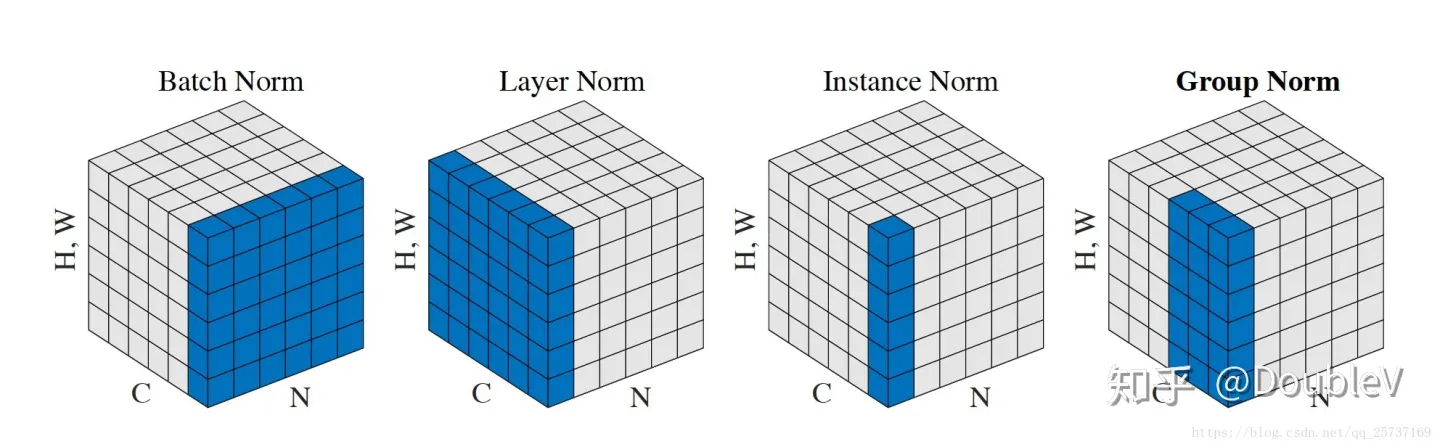
最后趁热打铁写一下GroupNorm和InstanceNorm,GroupNorm是介于IN和LN之间的一种算法,下图蓝色部分是每次要算均值和方差的数:
import torch
import torch.nn as nn
def layer_norm_process(input: torch.tensor, normalize_shape, eps=1e-5):
#pytorch实现中还有elementwise_affine,为true的情况下用来学习weight和bias
normalize_shape_len = len(normalize_shape)
#layernorm传入的是倒数几维要Normalize的shape
assert input.size()[-normalize_shape_len:] == normalize_shape
# 如果normalized_shape是3,那么torch.var_mean的dim就是-1
var_mean = torch.var_mean(input, dim= tuple([i for i in range(-normalize_shape_len, 0, 1)]), unbiased=False)
#不带unbiase=False结果会有所不同
var,mean = var_mean[0],var_mean[1]
res = (input-mean[(...,)+(None,)*normalize_shape_len])/torch.sqrt(var[(...,)+(None,)*normalize_shape_len]+eps)
return res
def main():
t = torch.rand(2, 3, 5) #文本[batch_size, seq_len, hidden_len];图片[batch_size, C, H*W]
ln = nn.LayerNorm(normalized_shape=(3,5), eps=1e-5)
gn = nn.GroupNorm(num_channels=3,num_groups=1, eps=1e-5)
#以下三个都是当LN用,GN在分成1个组的情况下就是LN,normalized_shape=(3,5),输出是一样的
print("ln:\n", ln(t))
print("my_ln:\n", layer_norm_process(t,(3,5), eps=1e-5))
print("gn:\n", gn(t))
#以下三个都是当成IN用,gn分组个数和num_channels一样的时候就是IN
ln_in = nn.LayerNorm(normalized_shape=(5), eps=1e-5)
gn_in = nn.GroupNorm(num_channels=3,num_groups=3, eps=1e-5)
in_in = nn.InstanceNorm1d(num_features=3, eps=1e-5) #InstanceNorm每次是对H*W个像素
print("t_ln_in:\n", ln_in(t))
print("t_gn_in:\n", gn_in(t))
print("t_in_in:\n", in_in(t))
if __name__ == '__main__':
main()
选择GN的理由:
- BN全名是Batch Normalization,见名知意,其是一种归一化方式,而且是以batch的维度做归一化,那么问题就来了,此归一化方式对batch是independent的,过小的batch size会导致其性能下降,一般来说每GPU上batch设为32最合适,但是对于一些其他深度学习任务batch size往往只有1-2,比如目标检测,图像分割,视频分类上,输入的图像数据很大,较大的batchsize显存吃不消
- 另外,Batch Normalization是在batch这个维度上Normalization,但是这个维度并不是固定不变的,比如训练和测试时一般不一样,一般都是训练的时候在训练集上通过滑动平均预先计算好平均-mean,和方差-variance参数,在测试的时候,不在计算这些值,而是直接调用这些预计算好的来用,但是,当训练数据和测试数据分布有差别是时,训练机上预计算好的数据并不能代表测试数据,这就导致在训练,验证,测试这三个阶段存在inconsistency。
选择IN的理由:
IN本身是一个非常简单的算法,尤其适用于批量较小且单独考虑每个像素点的场景中,因为其计算归一化统计量时没有混合批量和通道之间的数据,对于这种场景下的应用,我们可以考虑使用IN。对于我们之前介绍过的图像风格迁移[2]这类的注重每个像素的任务来说,每个样本的每个像素点的信息都是非常重要的,于是像BN[3]这种每个批量的所有样本都做归一化的算法就不太适用了,因为BN计算归一化统计量时考虑了一个批量中所有图片的内容,从而造成了每个样本独特细节的丢失。同理对于LN[4]这类需要考虑一个样本所有通道的算法来说可能忽略了不同通道的差异,也不太适用于图像风格迁移这类应用。
另外需要注意的一点是在图像这类应用中,每个通道上的值是比较大的,因此也能够取得比较合适的归一化统计量。但是有两个场景建议不要使用IN:
- MLP或者RNN中:因为在MLP或者RNN中,每个通道上只有一个数据,这时会自然不能使用IN;
- Feature Map比较小时:因为此时IN的采样数据非常少,得到的归一化统计量将不再具有代表性。
再写一点关于SyncBN、Shuffle BN、RMSNorm和DeepNorm
Synchronized Batch Normalization (SyncBN) is a type of batch normalization used for multi-GPU training. Standard batch normalization only normalizes the data within each device (GPU). SyncBN normalizes the input within the whole mini-batch.
MoCo V1中就使用了Shuffling BN的操作。BN大部分的时候是在当前GPU上算的,使用BN的时候BN的running mean和runnning variance很容易让模型找到正确的解。Shuffling BN就是算之前先把样本顺序打乱,送到多卡上,算完再合在一起
RMS Norm(来自于https://arxiv.org/pdf/1910.07467.pdf)全称是Root Mean Square Layer Normalization,与RMS Norm是基于LN的一种变体,主要是去掉了减去均值的部分,计算公式如下:

相比Layer Norm,RMS Norm不论是分母的方差和分子不分,都取消了均值计算,经作者在各种场景中实验发现,减少约 7%∼64% 的计算时间。
DeepNorm来自于微软DeepNet这篇文章,可以参考 Deepnet训练1000层的Transformer究竟有什么困难?-优快云博客
DeepNorm在执行Post LayerNorm之前使用常数α来对输入x的值进行放大
参考文献
[1] https://jiafulow.github.io/blog/2021/01/29/moving-average-in-batch-normalization/
[2] https://zhuanlan.zhihu.com/p/33173246
[3] https://www.zhihu.com/question/395811291
[4] https://www.zhihu.com/question/395811291/answer/1260290120
[5] https://www.zhihu.com/question/395811291/answer/1251829041
[6] https://zhuanlan.zhihu.com/p/242086547
最后转载一个pytorch的代码感受感受:
"""
View more, visit my tutorial page: https://mofanpy.com/tutorials/
My Youtube Channel: https://www.youtube.com/user/MorvanZhou
Dependencies:
torch: 0.4
matplotlib
numpy
"""
import torch
from torch import nn
from torch.nn import init
import torch.utils.data as Data
import matplotlib.pyplot as plt
import numpy as np
# torch.manual_seed(1) # reproducible
# np.random.seed(1)
# Hyper parameters
N_SAMPLES = 2000
BATCH_SIZE = 64
EPOCH = 12
LR = 0.03
N_HIDDEN = 8
ACTIVATION = torch.tanh
B_INIT = -0.2 # use a bad bias constant initializer
# training data
x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise
# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise
train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x = torch.from_numpy(test_x).float()
test_y = torch.from_numpy(test_y).float()
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
# show data
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')
class Net(nn.Module):
def __init__(self, batch_normalization=False):
super(Net, self).__init__()
self.do_bn = batch_normalization
self.fcs = []
self.bns = []
self.bn_input = nn.BatchNorm1d(1, momentum=0.5) # for input data
for i in range(N_HIDDEN): # build hidden layers and BN layers
input_size = 1 if i == 0 else 10
fc = nn.Linear(input_size, 10)
#这里因为所有层都必须是nn.Module的成员变量
setattr(self, 'fc%i' % i, fc) # IMPORTANT set layer to the Module
self._set_init(fc) # parameters initialization
self.fcs.append(fc)
if self.do_bn:
bn = nn.BatchNorm1d(10, momentum=0.5)
setattr(self, 'bn%i' % i, bn) # IMPORTANT set layer to the Module
self.bns.append(bn)
self.predict = nn.Linear(10, 1) # output layer
self._set_init(self.predict) # parameters initialization
def _set_init(self, layer):
init.normal_(layer.weight, mean=0., std=.1)
init.constant_(layer.bias, B_INIT)
def forward(self, x):
pre_activation = [x]
if self.do_bn: x = self.bn_input(x) # input batch normalization
layer_input = [x]
for i in range(N_HIDDEN):
x = self.fcs[i](x)
pre_activation.append(x)
if self.do_bn: x = self.bns[i](x) # batch normalization
x = ACTIVATION(x)
layer_input.append(x)
out = self.predict(x)
return out, layer_input, pre_activation
nets = [Net(batch_normalization=False), Net(batch_normalization=True)]
print(*nets) # print net architecture
opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]
loss_func = torch.nn.MSELoss()
def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):
[a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]
if i == 0:
p_range = (-7, 10);the_range = (-7, 10)
else:
p_range = (-4, 4);the_range = (-1, 1)
ax_pa.set_title('L' + str(i))
ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='#FF9359', alpha=0.5);ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='#74BCFF', alpha=0.5)
ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='#FF9359');ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='#74BCFF')
for a in [ax_pa, ax, ax_pa_bn, ax_bn]: a.set_yticks(());a.set_xticks(())
ax_pa_bn.set_xticks(p_range);ax_bn.set_xticks(the_range)
axs[0, 0].set_ylabel('PreAct');axs[1, 0].set_ylabel('BN PreAct');axs[2, 0].set_ylabel('Act');axs[3, 0].set_ylabel('BN Act')
plt.pause(0.01)
if __name__ == "__main__":
f, axs = plt.subplots(4, N_HIDDEN + 1, figsize=(10, 5))
plt.ion() # something about plotting
plt.show()
# training
losses = [[], []] # recode loss for two networks
for epoch in range(EPOCH):
print('Epoch: ', epoch)
layer_inputs, pre_acts = [], []
for net, l in zip(nets, losses):
net.eval() # set eval mode to fix moving_mean and moving_var
pred, layer_input, pre_act = net(test_x)
l.append(loss_func(pred, test_y).data.item())
layer_inputs.append(layer_input)
pre_acts.append(pre_act)
net.train() # free moving_mean and moving_var
plot_histogram(*layer_inputs, *pre_acts) # plot histogram
for step, (b_x, b_y) in enumerate(train_loader):
for net, opt in zip(nets, opts): # train for each network
pred, _, _ = net(b_x)
loss = loss_func(pred, b_y)
opt.zero_grad()
loss.backward()
opt.step() # it will also learns the parameters in Batch Normalization
plt.ioff()
# plot training loss
plt.figure(2)
plt.plot(losses[0], c='#FF9359', lw=3, label='Original')
plt.plot(losses[1], c='#74BCFF', lw=3, label='Batch Normalization')
plt.xlabel('step');plt.ylabel('test loss');plt.ylim((0, 2000));plt.legend(loc='best')
# evaluation
# set net to eval mode to freeze the parameters in batch normalization layers
[net.eval() for net in nets] # set eval mode to fix moving_mean and moving_var
preds = [net(test_x)[0] for net in nets]
plt.figure(3)
plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='#FF9359', lw=4, label='Original')
plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='#74BCFF', lw=4, label='Batch Normalization')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')
plt.legend(loc='best')
plt.show()






















 2748
2748

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








