先说求偏导的几种情况：
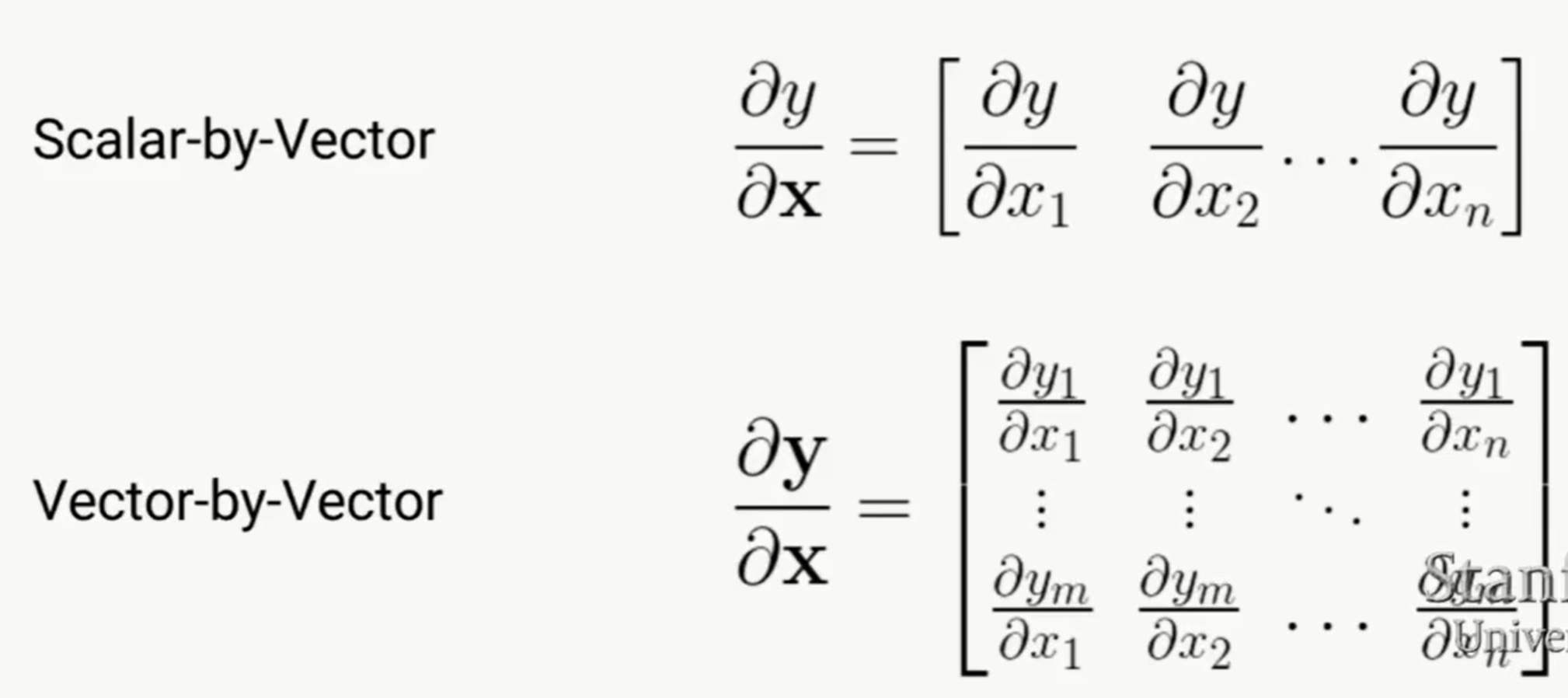
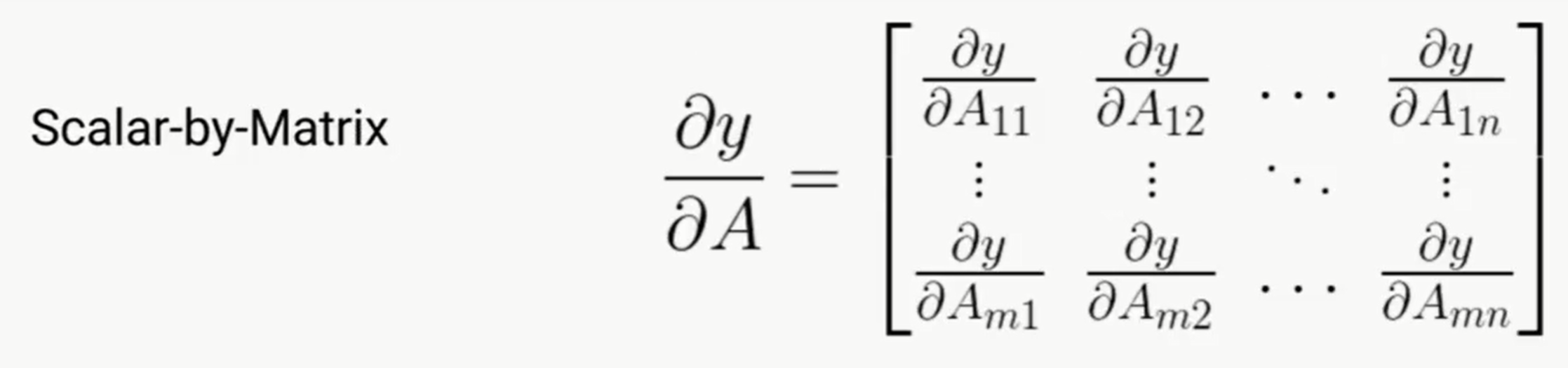
几个值得注意的点：
1. 注意vector by vector，如果y是m*1,x是n*1，那么偏导结果的shape是m*n
2. 所有Scalar by vector、Scale by Maxtrix这些，结果的shape都是和denominator的shape一样的。而且对于deep learning来说，基本上是loss对某个参数的偏导，所以理解这个就很有用
3. 可以vector by matrix，但是定义之后就是个3维数组了，实际用的基本上就是loss对某个参数的偏导
当涉及到梯度传播的chain rule时，由于loss对W和X的偏导左右乘转置的关系不一致，而且不太好记，所以弄了这么一个"Dimension Balancing"的方式，反正loss对W和X的偏导结果的shape是m*w，和下图中的delta的shape相同，在已知W、X和Z的shape的情况下，就可以准确推断出loss对W和X的偏导的结果
当存在激活函数的时候，注意下面的z和h都是分别是长度为n的向量
这时Loss对hidden layer的loss可以用hadamard product（其实就是逐对乘，圆圈记号）或者对角矩阵的方式去表达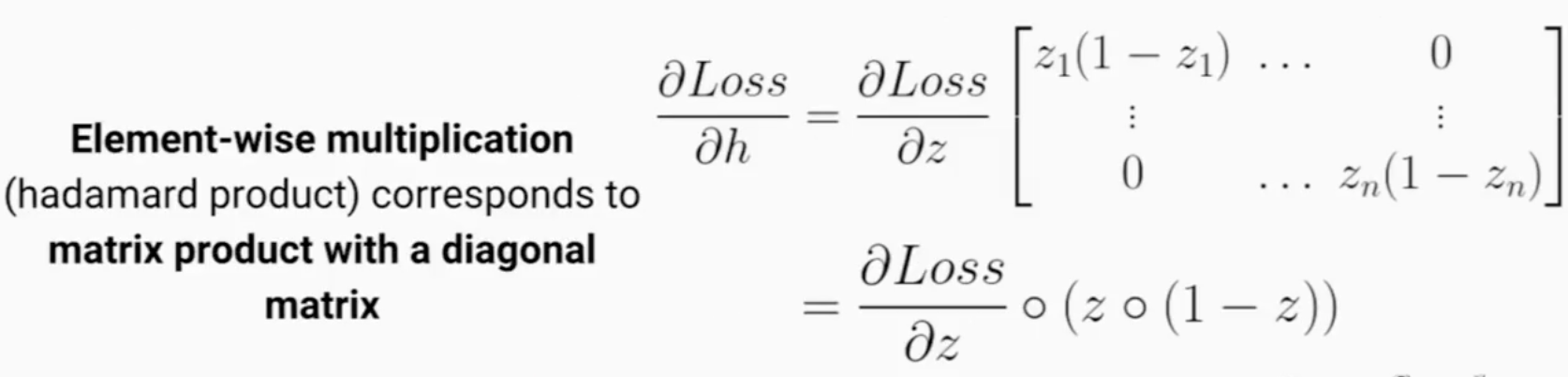
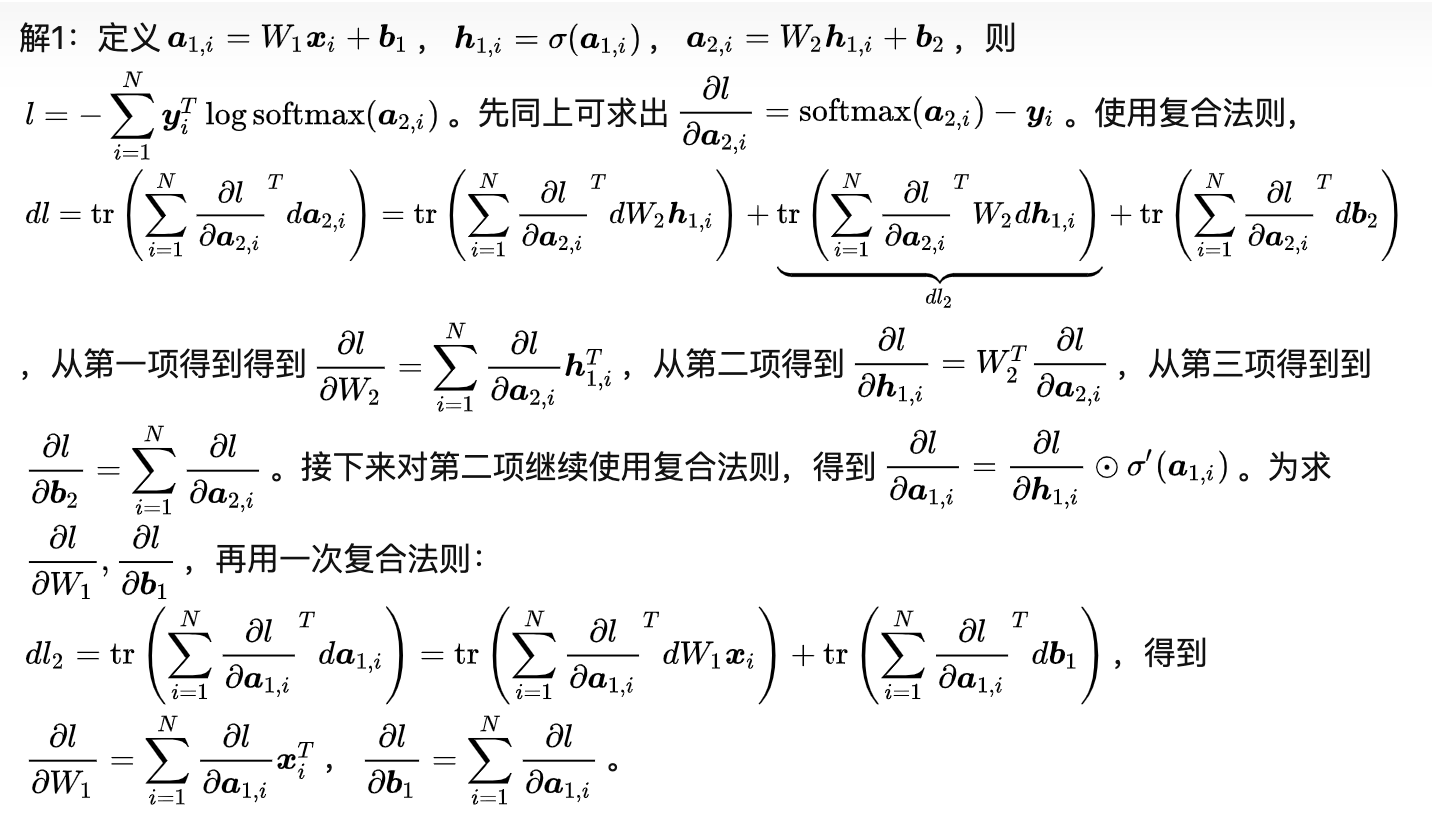
关于"Dimension Balancing"的推导实际上比较简单，就是转置有点绕（例如下图），所以干脆不饶了，知道这个Dimension Balancing的策略方便快速理解shape
机器学习中还有很多梯度的推导，可以利用trace来回避转置不停绕的问题，例如PCA的推导：
其他矩阵求导的场景还有很多，下面转俩博客：
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
