基于频域滤波的图像恢复

实验一：基于傅里叶变换的图像低通滤波实践解析

 一、引言：频域滤波的魅力

在数字图像处理领域，傅里叶变换犹如一把打开频域大门的钥匙。通过将图像从空间域转换到频率域，我们可以直观地观察到图像中不同频率成分的分布，并通过滤波操作实现图像增强、噪声消除等效果。本文将通过Python代码实例，带您领略频域滤波的神奇力量。

二、环境准备与核心库介绍

OpenCV：计算机视觉核心库，提供高效的图像处理函数

NumPy：科学计算基础库，处理多维数组的利器

Matplotlib：数据可视化工具，支持高质量的图像显示

三、核心算法流程解析

3.1 图像预处理与傅里叶变换

归一化处理：将像素值映射到[0,1]范围

DFT变换：将空间域转换为复数形式的频域表示

频谱中心化：将低频分量移至频谱图中心

3.2低通滤波器构建

理想低通滤波器：以中心为原点，半径D0的圆形区域

数学表达式：

3.3. 频域滤波与逆变换

频域相乘等效于空间域卷积

逆变换恢复空间域图像

幅度计算获取最终结果

四、效果对比与可视化

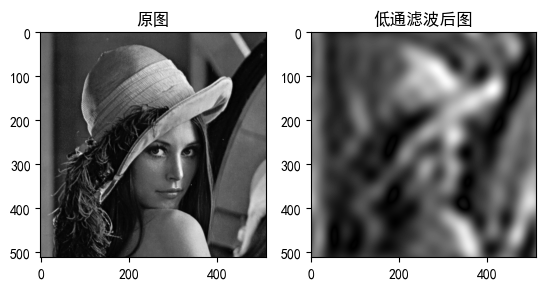
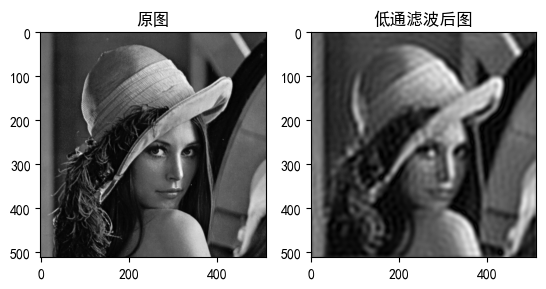
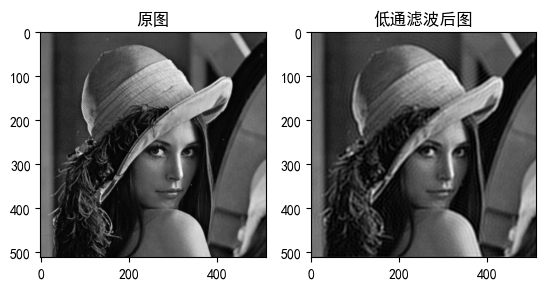
处理效果分析：1.图像边缘模糊化；2.高频细节被抑制；3.整体呈现平滑效果

五、关键参数影响分析

截止频率	图像效果	信息保留
D0=10	严重模糊	主要轮廓
D0=30	适度平滑	基本特征
D0=60	轻微模糊	丰富细节

六.代码展示

import cv2
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei'] 
plt.rcParams['axes.unicode_minus'] = False 
# 以灰度模式读取指定路径的图像
img=cv2.imread('001.bmp',0)

# 对图像进行归一化处理（除以255），然后使用OpenCV的离散傅里叶变换函数进行变换，输出复数形式
img_f=cv2.dft(img/255,flags=cv2.DFT_COMPLEX_OUTPUT)
# 将傅里叶变换后的结果进行移频操作，把低频部分移到图像中心
img_f=np.fft.fftshift(img_f)
# 计算傅里叶变换结果的幅度谱，并进行对数变换以增强显示效果
magnitude_spectrum=20*np.log(cv2.magnitude(img_f[:,:,0],img_f[:,:,1]))

# 定义低通滤波器的截止频率
D0=30

# 创建一个与输入图像形状相同的全零数组，用于存储低通滤波器
H=np.zeros(img.shape)

# 计算图像的中心坐标
w,h=img.shape[0]//2,img.shape[1]//2

# 遍历图像的每一个像素
for i in range(img.shape[0]):
    for j in range(img.shape[1]):
        # 计算当前像素到图像中心的距离
        if(np.sqrt((i-w)**2+(j-h)**2))<=D0:
            # 如果距离小于等于截止频率，则该位置的滤波器值设为1
            H[i,j]=1
        else:
            # 否则，该位置的滤波器值设为0
            H[i,j]=0
# 将傅里叶变换结果的实部与低通滤波器相乘
img_f[:,:,0]=img_f[:,:,0]*H
# 将傅里叶变换结果的虚部与低通滤波器相乘
img_f[:,:,1]=img_f[:,:,1]*H
# 对滤波后的结果进行逆移频操作，恢复原来的频域分布
img_f=np.fft.ifftshift(img_f )
# 对滤波后的频域结果进行逆离散傅里叶变换，得到空域图像
img_n=cv2.idft(img_f)
# 计算逆变换结果的幅度，得到最终的图像
img_n=cv2.magnitude(img_n[:,:,0],img_n[:,:,1])
# 创建一个1行2列的子图布局，并选择第1个子图
plt.subplot(121)
# 显示原始灰度图像
plt.imshow(img,'gray')
# 设置第1个子图为“原图”
plt.title('原图')
# 选择第2个子图
plt.subplot(122)
# 显示低通滤波后的灰度图像
plt.imshow(img_n,'gray')
# 设置第2个子图为“低通滤波后图”
plt.title('低通滤波后图')
# 显示
plt.show()

七.实验小结

通过本文的实践解析，我们不仅掌握了基于傅里叶变换的频域滤波实现方法，更深入理解了数字图像处理的核心原理。这种频域分析方法为后续的图像增强、特征提取等高级处理奠定了重要基础。

实验二：基于傅里叶变换的图像高通滤波实践解析

一.引言：从低通到高通，频域滤波的双面性

在频域滤波中，低通滤波与高通滤波是相辅相成的两种核心操作。低通滤波通过保留低频成分实现平滑降噪，而高通滤波则通过抑制低频、保留高频成分凸显图像细节和边缘特征。本文将以Python代码实现为基础，深入解析高通滤波的实现原理与应用场景。

二、环境配置与代码框架

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 中文显示配置
plt.rcParams['font.sans-serif'] = ['SimHei'] 
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('001.bmp', 0)

三、核心算法实现流程

3.1 傅里叶变换与频域中心化

img_f = cv2.dft(img/255, flags=cv2.DFT_COMPLEX_OUTPUT)
img_f = np.fft.fftshift(img_f)  # 低频移至中心

归一化处理：将像素值映射到[0,1]范围，避免数值溢出

fftshift操作：将低频分量移至频谱图中心（图1左→右）

3.2 理想高通滤波器构建

D0 = 50  # 截止频率
H = np.zeros(img.shape)
w, h = img.shape[0]//2, img.shape[1]//2  # 中心坐标

for i in range(img.shape[0]):
    for j in range(img.shape[1]):
        if np.sqrt((i-w)**2 + (j-h)**2) > D0:  # 距离判断
            H[i,j] = 1  # 高频区域保留

数学表达式：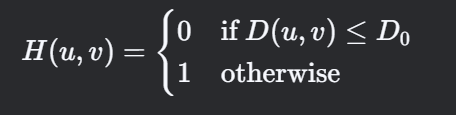

3.3 频域滤波与逆变换

# 频域滤波
img_f[:,:,0] *= H  # 实部滤波
img_f[:,:,1] *= H  # 虚部滤波

# 逆变换复原图像
img_f = np.fft.ifftshift(img_f)  # 移频还原
img_n = cv2.idft(img_f)  # 逆傅里叶变换
img_n = cv2.magnitude(img_n[:,:,0], img_n[:,:,1])  # 计算幅度

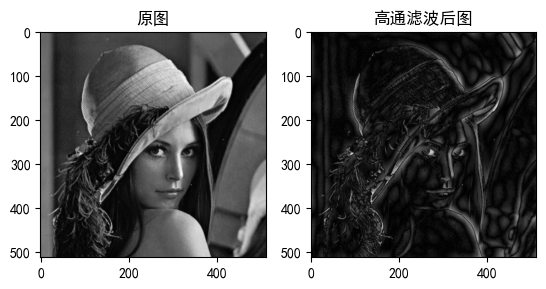
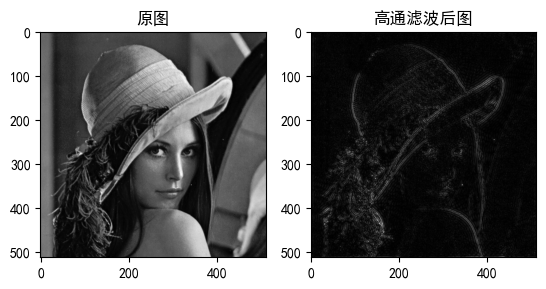
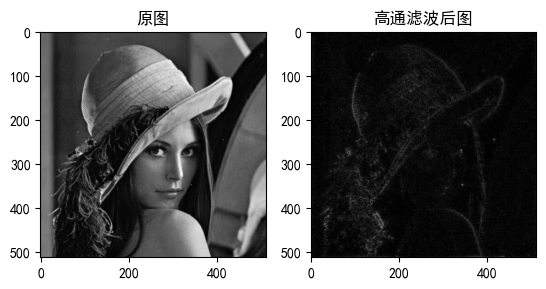
四、效果对比与分析

处理效果特征：

1.边缘轮廓显著增强；

2.纹理细节更加突出；

3.整体亮度降低（低频分量被抑制）。

五、参数影响与选择策略

截止频率(D0)	边缘锐度	细节保留	适用场景
10	过度增强	噪声明显	轮廓提取
50	适中	平衡	通用增强
100	微弱	低频残留	轻微锐化

六.代码完全展示

# 导入OpenCV库
import cv2
# 导入NumPy库
import numpy as np
# 导入Matplotlib绘图库
import matplotlib.pyplot as plt
# 以灰度模式读取图像
img=cv2.imread('001.bmp',0)
# 图像归一化并做离散傅里叶变换
img_f=cv2.dft(img/255,flags=cv2.DFT_COMPLEX_OUTPUT)
# 频域移频，低频置中
img_f=np.fft.fftshift(img_f)
# 定义高通截止频率
D0=50
# 创建全零高通滤波器
H=np.zeros(img.shape)
# 计算图像中心坐标
w,h=img.shape[0]//2,img.shape[1]//2
# 遍历图像像素
for i in range(img.shape[0]):
    for j in range(img.shape[1]):
        # 计算距中心距离，若小于等于截止频率
        if(np.sqrt((i-w)**2+(j-h)**2))<=D0:
            # 滤波器值设为0
            H[i,j]=0
        else:
            # 否则设为1
            H[i,j]=1
# 实部与滤波器相乘
img_f[:,:,0]=img_f[:,:,0]*H
# 虚部与滤波器相乘
img_f[:,:,1]=img_f[:,:,1]*H
# 逆移频
img_f=np.fft.ifftshift(img_f )
# 逆离散傅里叶变换
img_n=cv2.idft(img_f)
# 计算幅度得最终图像
img_n=cv2.magnitude(img_n[:,:,0],img_n[:,:,1])
# 选第1个子图
plt.subplot(121)
# 显示原图
plt.imshow(img,'gray')
# 设置第1个子图标题
plt.title('原图')
# 选第2个子图
plt.subplot(122)
# 显示滤波后图
plt.imshow(img_n,'gray')
# 设置第2个子图标题
plt.title('高通滤波后图')
# 显示图像
plt.show()

七.实验小结

通过本文的完整实现与解析，读者可以深入理解频域滤波的核心思想，掌握高通滤波在图像处理中的实际应用。高频分量承载着图像的细节灵魂，合理利用这一特性，将为后续的图像分析任务提供强大的特征支持。