数字图像处理个人练习04--图像复原

图像复原的基本原理

图像的复原就是要尽可能恢复退化图像的本来⾯⽬，它是沿图像降质的逆向过程进⾏。典型的图像复原是根据图像退化的先验知识建⽴⼀个退化模型，以此模型为础，采⽤各种逆退化处理⽅法进⾏恢复，使图像质量得到改善

---

频域常用的图像恢复方法有哪两种？简述他们的处理方法和步骤。

频域常⽤的图像恢复⽅法有逆滤波和维纳滤波。

逆滤波

逆滤波是最早使⽤的⼀种⽆约束复原⽅法
在图像复原中，给定$g(x,y)$ 和关于退化函数$H$ 的⼀些知识以及外加噪声项$\eta (x,y)$ ，得到原始图
像$f(x,y)$ 的近似估计$\hat{f}(x,y)$

$$G(u,v)=H(u,v)F(u,v)$$
G,H,F分别是退化图像g,点扩散函数h,原始图像f的傅里叶变换

有噪声的情况下是如下形式
$$G(u,v)=H(u,v)F(u,v)+n(u,v)$$

根据对退化系统的点扩散函数$h(x,y)$和噪声函数的了解，在误差最⼩的情况下，利⽤它们的傅⽴叶变换$H(u,v)$ 和$n(u,v)$ 进⾏估计，如下式所示

$$\hat{F}(u,v)=\frac{G(u,v)}{H(u,v)}=F(u,v)+\frac{n(u,v)}{H(u,v)}$$

得到$\hat{F}$之后通过求他的反变换，得到复原图像

逆滤波复原的步骤是

1. 对于退化图像$g(x,y)$ 求⼆维傅⽴叶变换$G(u,v)$
2. 计算$h(x,y)$ 的⼆维傅⽴叶变换$H(u,v)$
3. ⽤$n(u,v)$ 产⽣随机噪声
4. ⽤上式计算$\hat{F}(u,v)$
5. 求$\hat{F}(u,v)$的反变换，即可得到复原图像

维纳滤波

维纳滤波器（wiener filtering) 的本质是使估计误差（定义为期望响应与滤波器实际输出之差）均方值最小化

而维纳滤波是假定图像信号可以近似看作平稳随机过程，建立在图像和噪声都是随机变量的基础之上，综合考虑退化函数和噪声统计特征两个⽅⾯因素设计滤波器，使得复原后的图像与原始图像之间的均⽅误差最⼩

计算公式为
$$\hat{F}(u,v)=\left[\frac{1}{H(u,v)}\times \frac{|H(u,v){|}^2}{|H(u,v){|}^2+S_f(u,v)/S_{\eta }(u,v)}\right]G(u,v)$$

1. $G(u,v)$为退化图像的傅⽴叶变换
2. $H(u,v)$ 是点扩散函数的傅⽴叶变换，
3. $S_{\eta }(u,v)=|N(u,v){|}^2$为噪声的功率谱
4. $S_f(u,v)=|F(u,v){|}^2$为退化图像的功率谱。

步骤

1. 对于退化图像$g(x,y)$ 求⼆维傅⽴叶变换$G(x,y)$
2. 点扩散函数$h(x,y)$ 的⼆维傅⽴叶变换$H(x,y)$
3. 计算噪声图像的功率谱$S_{\eta }(u,v)$ 和退化图像的功率谱$S_f(u,v)$
4. ⽤上式计算
5. 求$F(u,v)$ 的反变换，即可得到复原图像

---

用维纳滤波器，逆滤波起和均值滤波器对图像进行复原和平滑，并对比结果

①实验环境配置

本次实验使用python语言，基于cv2来进行图片的输入输出，基于numpy对图片矩阵进行傅里叶变换以及滤波的处理

import numpy as np
import cv2

②实验基本思路与步骤

1. 对图像进行模糊处理，并得到自己的模糊函数
2. 通过逆滤波和维纳滤波进行逆变换模拟原来的图像
3. 再通过图片平滑进行比对

③核心函数

def mat_motion_blur(image, alpha):

传入初始函数图像以及运动模糊的alpha角度
返回经过运动模糊变化的斜率矩阵

def make_blur(mat, image, epsilon):

产生模糊的图像，第一个为模糊矩阵，第二个为要处理的图片，第三个为误差

def inverse(mat, image, epsilon):

逆滤波进行图像处理

def wiener(mat, image, epsilon, k = 0.01):

维纳滤波进行图像处理，此处k表示S_f/S_eta

def mean(image, str):

进行平滑处理并进行图像输出

④实验效果

角度为60°且epsilon = 0.01的模糊图像，利用逆滤波进行复原并平滑后的对比图

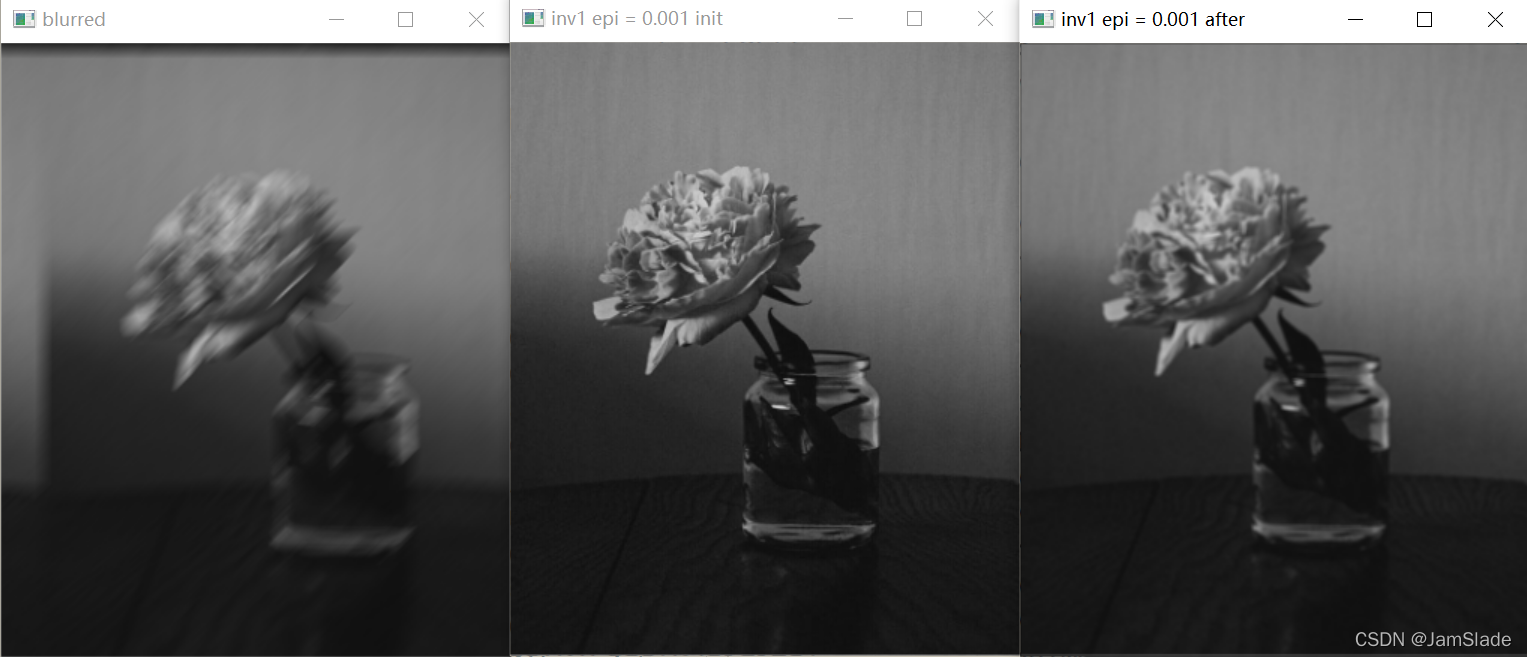
角度为60°且epsilon = 0.01的模糊图像，利用维纳滤波进行复原并平滑后的对比图

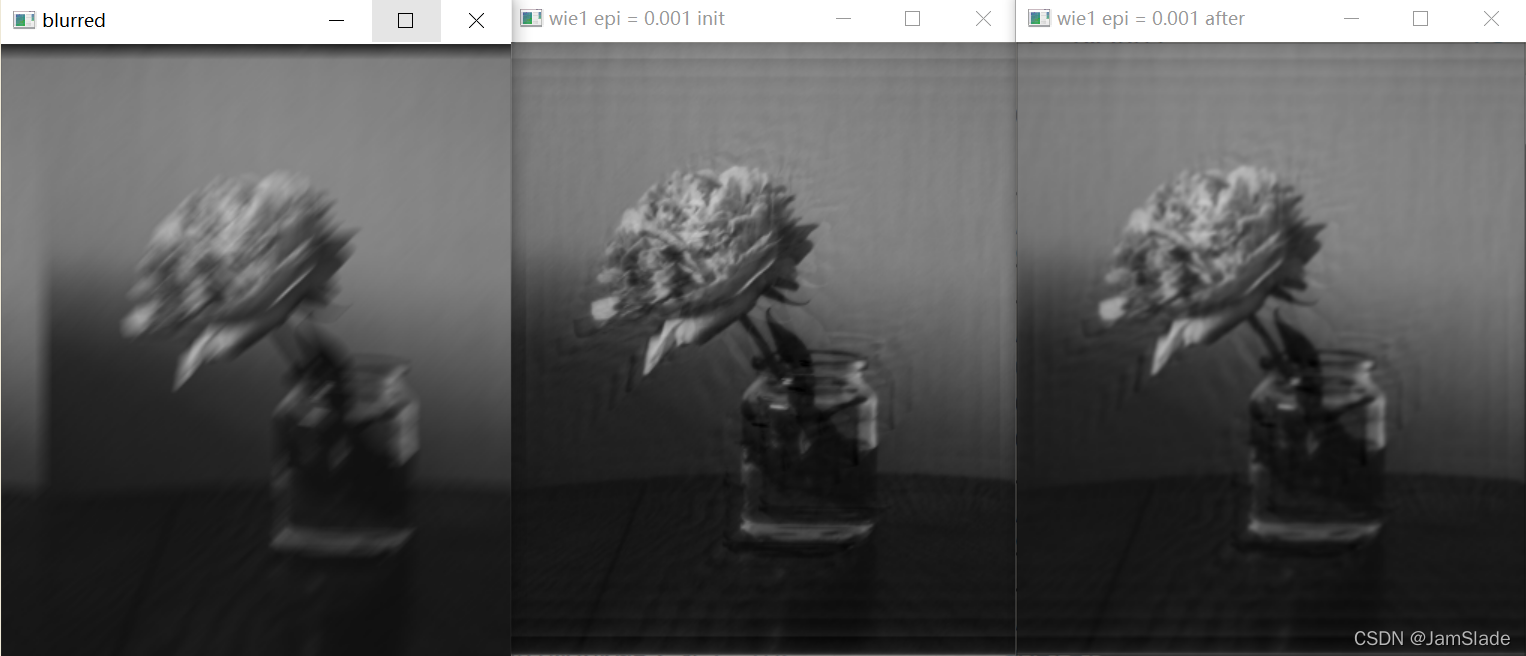
加入随机噪声后epsilon = 0.25的逆滤波图像还原

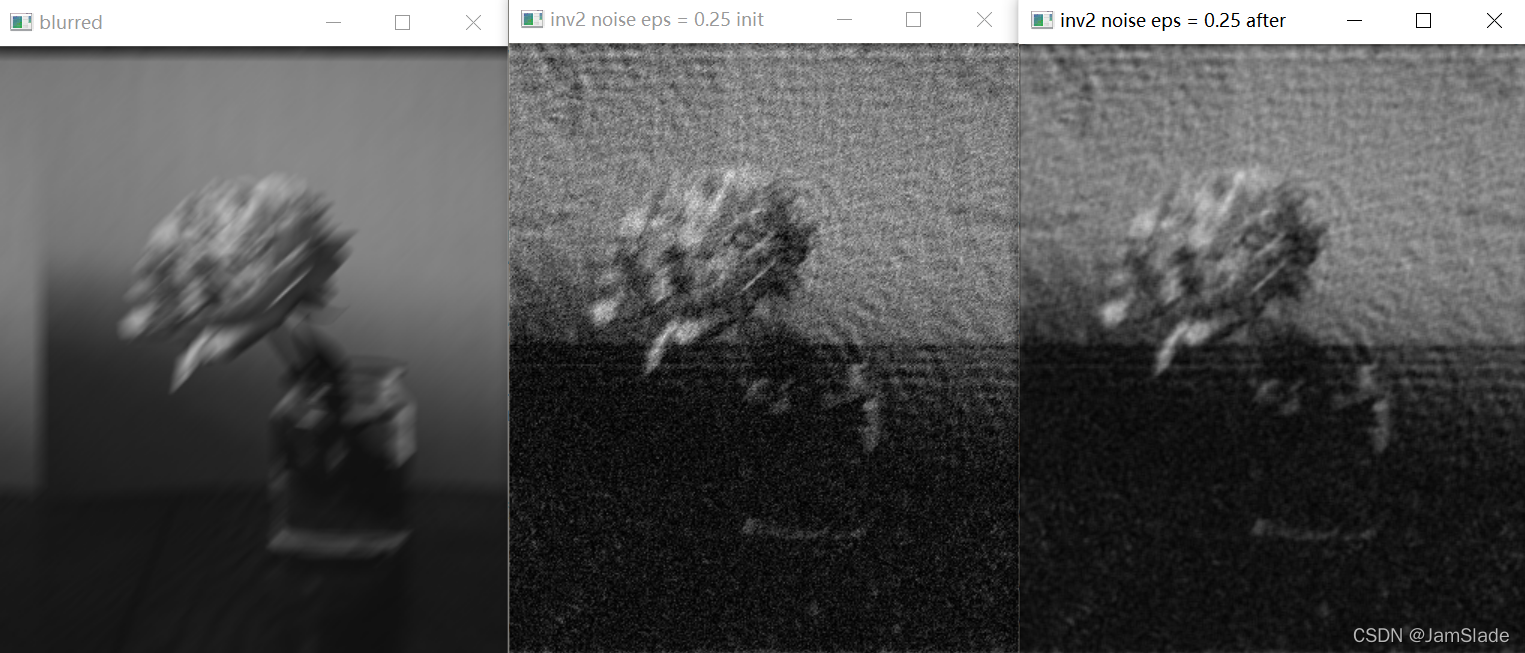
加入随机噪声后epsilon = 0.15的逆滤波图像还原

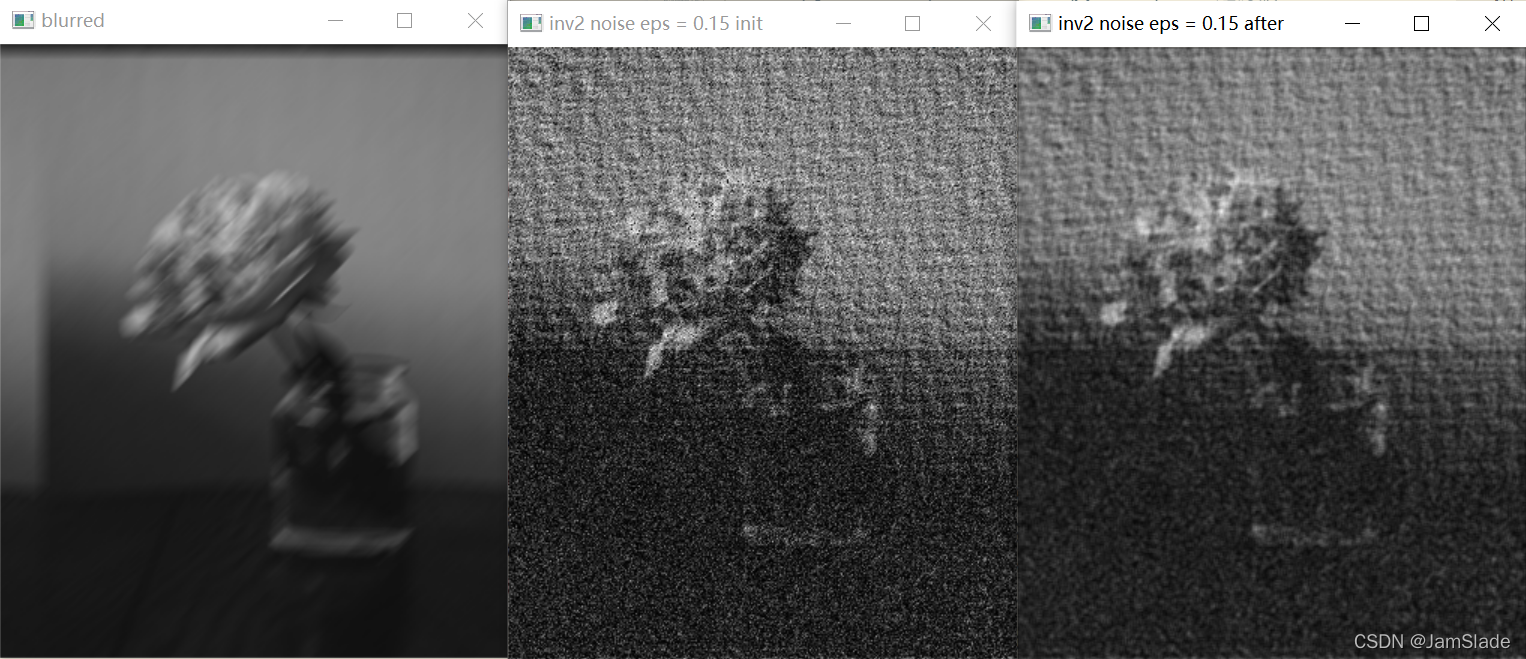
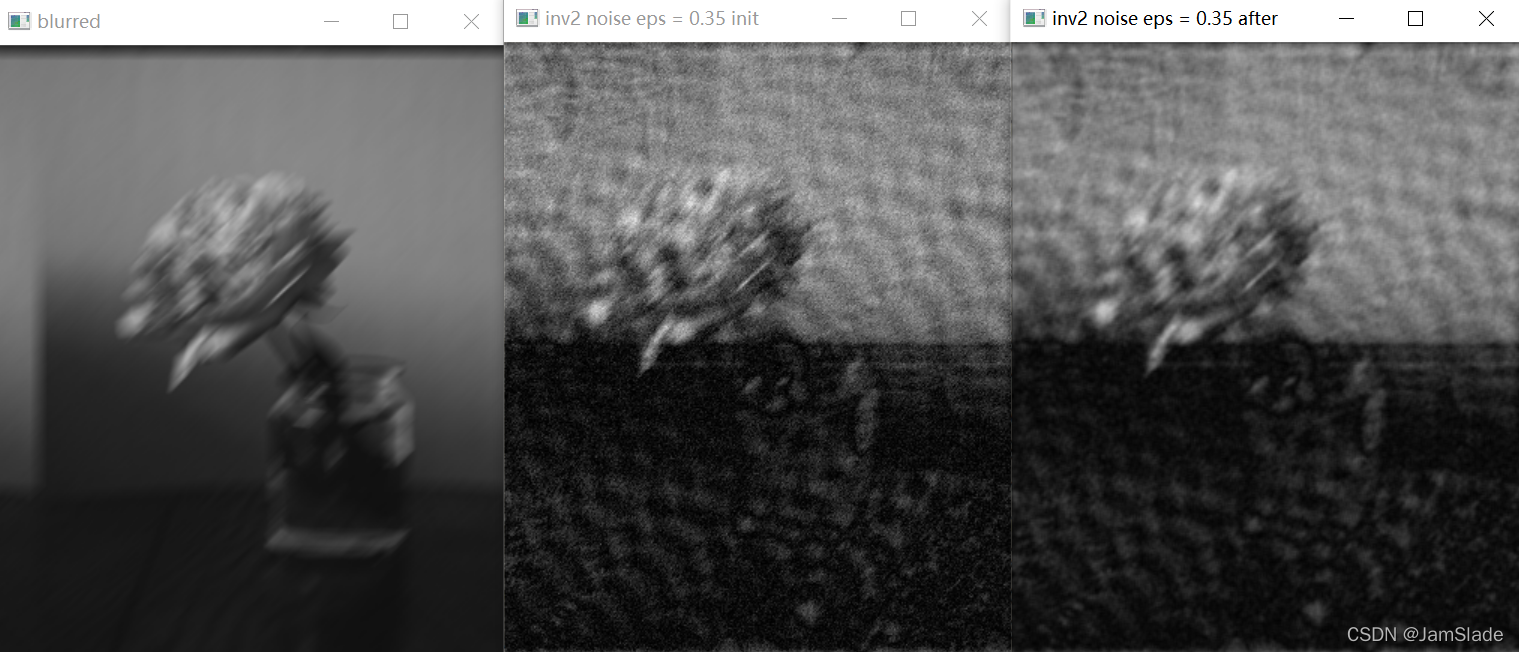
加入随机噪声后epsilon = 0.35的逆滤波图像还原

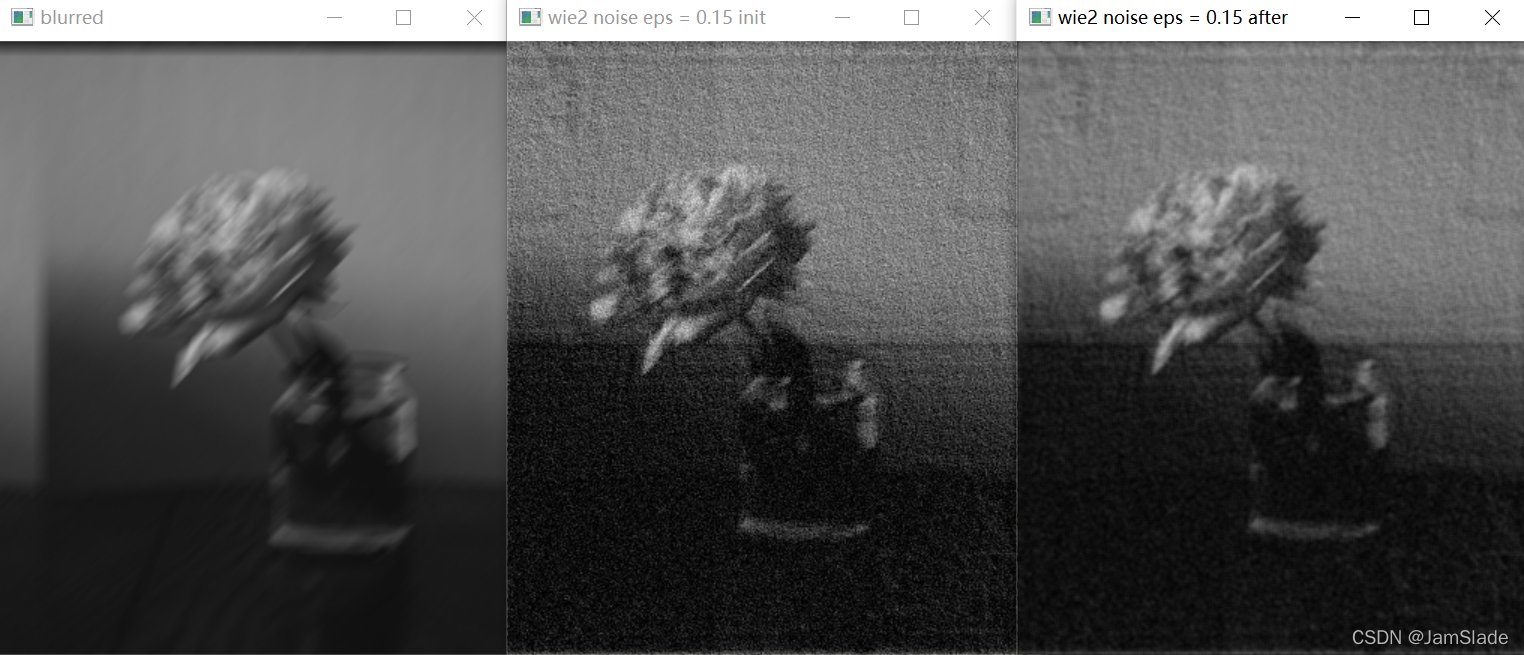
加入随机噪声后epsilon = 0.15的维纳滤波图像还原

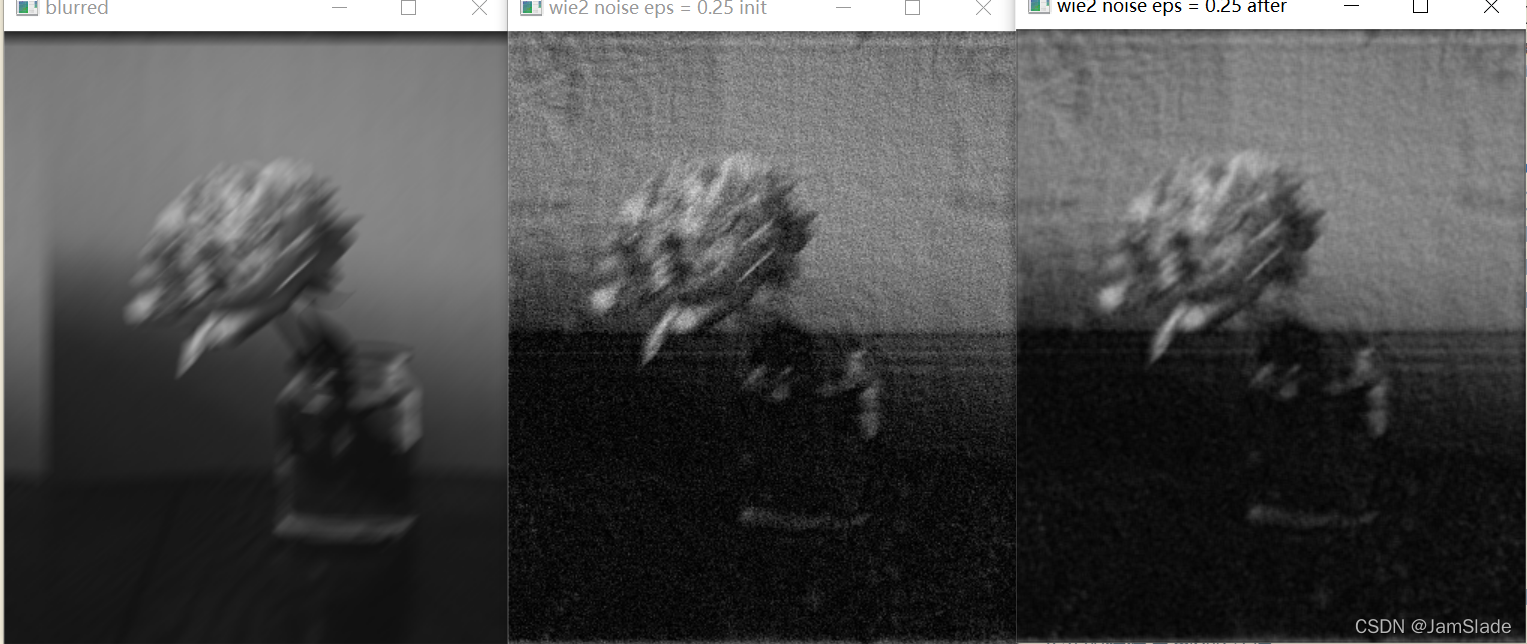
加入随机噪声后epsilon = 0.25的维纳滤波图像还原

⑤整合代码

import numpy as np
import cv2

class image_restoration():
    def mat_motion_blur(image, alpha):
        #对一个角度进行运动模糊处理
        height, width = image.shape[:2]
        mat = np.zeros((height, width))
        center = (height - 1)/2
        tangent = np.tan(alpha * np.pi / 180)

        if tangent <= 1:
            for i in range(20):
                offset = np.round(i * tangent)
                mat[int(center + offset), int(center - offset)] = 1
        else:
            for i in range(20):
                offset = np.round(i * 1 / tangent)
                mat[int(center + offset), int(center - offset)] = 1
        # 可以理解为退化函数
        return mat / mat.sum()
    
    def make_blur(mat, image, epsilon):
        # 产生退化图片g(x,y)
        mat_fft = np.fft.fft2(mat)
        # 矩阵傅里叶变换
        image_fft = np.fft.fft2(image) + epsilon
        # 图像傅里叶变换
        blurred = np.fft.ifft2(mat_fft * image_fft)
        # 运动模糊后变化
        ## g(x,y) = Hf(x,y)+n(x,y)
        blurred = np.abs(np.fft.fftshift(blurred))
        # 对fft的部分进行定义域的调整
        return blurred

    def inverse(mat, image, epsilon):
        mat_fft = np.fft.fft2(mat)
        # G(u,v)
        image_fft = np.fft.fft2(image) + epsilon
        # H(u,v)
        restore = np.fft.ifft2(mat_fft / image_fft)
        #区别在于乘除 F(u,v)
        restore = np.abs(np.fft.fftshift(restore))
        return restore
    def wiener(mat, image, epsilon, k = 0.01):
        mat_fft = np.fft.fft2(mat)#G
        image_fft = np.fft.fft2(image) + epsilon# H
        image_fft_eta = np.conj(image_fft) / (np.abs(image_fft) ** 2 + k)
        # 左边整个式子 用k表示S_f/ S_η
        restore = np.fft.ifft2(mat_fft * image_fft_eta)
        restore = np.abs(np.fft.fftshift(restore))
        return restore
    def mean(image, str):

        cv2.imshow(str+' init', np.uint8(image))
        mat = np.array([
            [1/9,1/9,1/9],
            [1/9,1/9,1/9],
            [1/9,1/9,1/9]
        ])
        #res = cv2.filter2D(image, -1, mat);
        #cv2.imshow("?",res)
        height, width = image.shape[:2]
        con = np.zeros((height+2, width+2))
        new_img = np.zeros_like(image,dtype=np.uint8)

        for y in range(height):
            for x in range(width):
                con[y+1][x+1] = image[y][x]
        for y in range(1,height+1):
            for x in range(1,width+1):
                new_img[y-1][x-1] = (
                    mat[0][0]*con[y+1][x+1] +  mat[0][1]*con[y+1][x] +  mat[0][2]*con[y+1][x-1]+
                    mat[1][0]*con[y][x+1] + mat[1][1]*con[y][x] +  mat[1][2]*con[y][x-1] + 
                    mat[2][0]*con[y-1][x+1] +  mat[2][1]*con[y-1][x] +  mat[2][2]*con[y-1][x-1]
                )
       
        cv2.imshow(str+" after", np.uint8(new_img))
        cv2.waitKey(0)

IR = image_restoration

def test():
    image = cv2.imread('pic4.png')
    image = cv2.cvtColor(image ,cv2.COLOR_BGR2GRAY)
    

    blur_mat = IR.mat_motion_blur(image, 60)
    
    blurred = np.abs(IR.make_blur(image, blur_mat, 0.001))
    way1 = IR.inverse(blurred, blur_mat, 0.001)
    way2 = IR.wiener(blurred, blur_mat, 0.001)

    noise = blurred + 0.1 * blurred.std() * np.random.standard_normal(blurred.shape)
    #print(noise)
    way3 = IR.inverse(noise, blur_mat, 0.35)
    way4 = IR.wiener(noise, blur_mat, 0.25)
    
    cv2.imshow('blurred',np.uint8(blurred))
    IR.mean(way4,'wie2 noise eps = 0.25')
   
    cv2.waitKey(0)
    

if __name__ == '__main__':
    test()