【Luogu P2607】[ZJOI2008] 骑士（树形dp）

题目

题目描述

Z 国的骑士团是一个很有势力的组织，帮会中汇聚了来自各地的精英。他们劫富济贫，惩恶扬善，受到社会各界的赞扬。

最近发生了一件可怕的事情，邪恶的 Y 国发动了一场针对 Z 国的侵略战争。战火绵延五百里，在和平环境中安逸了数百年的 Z 国又怎能抵挡的住 Y 国的军队。于是人们把所有的希望都寄托在了骑士团的身上，就像期待有一个真龙天子的降生，带领正义打败邪恶。

骑士团是肯定具有打败邪恶势力的能力的，但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士（当然不是他自己），他是绝对不会与自己最厌恶的人一同出征的。

战火绵延，人民生灵涂炭，组织起一个骑士军团加入战斗刻不容缓！国王交给了你一个艰巨的任务，从所有的骑士中选出一个骑士军团，使得军团内没有矛盾的两人（不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况），并且，使得这支骑士军团最具有战斗力。

为了描述战斗力，我们将骑士按照 $1$ 至 $n$ 编号，给每名骑士一个战斗力的估计，一个军团的战斗力为所有骑士的战斗力总和。

输入格式

第一行包含一个整数 $n$，描述骑士团的人数。

接下来 $n$ 行，每行两个整数，按顺序描述每一名骑士的战斗力和他最痛恨的骑士。

输出格式

应输出一行，包含一个整数，表示你所选出的骑士军团的战斗力。

输入输出样例

输入 #1
3
10 2
20 3
30 1
输出 #1
30

说明/提示

数据规模与约定

对于 $30\%$ 的测试数据，满足 $n\le 10$；

对于 $60\%$ 的测试数据，满足 $n\le 100$；

对于 $80\%$ 的测试数据，满足 $n\le 10^4$；

对于 $100\%$ 的测试数据，满足 $1\le n\le 10^6$，每名骑士的战斗力都是不大于 $10^6$ 的正整数。

思路

把每个骑士和他憎恨的骑士连边。
可以发现，有很多联通块，每个联通块里点数与边数相等，所以有且只有一个环。
也就是说，每一个联通块都是一个基环树。
就长这样：

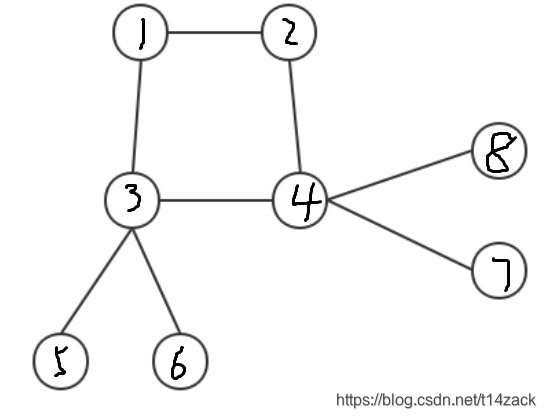
那么对于每个联通块，我们只需把环上的某一条边断掉：

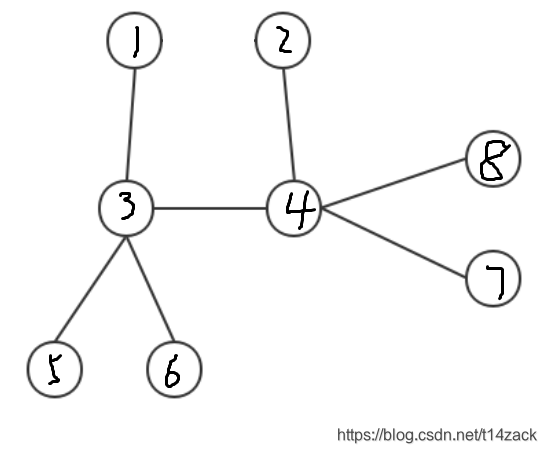
然后对于断开的两个端点 $dx,dy$（图中为 $1$，$2$），分别跑“没有上司的舞会”，找出 $max(dp[dx][0],dp[dy][0])$，累加进 $ans$ 即可。

注意：
$1.$ 要开 long long（吧）。
$2.$ 断边是要记录边的编号，不能只记录两个端点，因为有可能会有两个点形成环的情况。

---

找环：
双向连边，如果入度为 $1$ 就进队列。
然后进行拓扑排序。
最后所有入度 $\ge 2$ 的边都是环上的边。（可以手动模拟一遍）

---

“没有上司的舞会”：
设 $dp[x][0/1]$ 位第 $x$ 号骑士选/不选的最大值。
如果不选 $x$，那么就是每个儿子选或不选的较大值之和。
如果选 $x$，那么就是所有 $x$ 的儿子都不选的最大值 $+$ $x$ 号的值 。
转移方程：
$dp[x][0]=\sum max(dp[y][0],d$