【C++】【算法】高精度加减乘除

最新推荐文章于 2025-03-31 12:32:12 发布

鼓浪屿Estelle

最新推荐文章于 2025-03-31 12:32:12 发布

阅读量1k

点赞数 17

文章标签： c++ 开发语言

本文链接：https://blog.youkuaiyun.com/sysfsv/article/details/145942563

版权

0 引言

在用C++写代码时，为了解决各种问题，我们会经常使用到加减乘除，我们对加减乘除运算也再熟悉不过。

但是，C++作为一门强类型语言，不管是使用short，int，亦或是long long，对数据存储范围都是有限的；

类型	大小	范围
short	2字节	-32768 ~ 32767
int	4字节	-2147483648~2147483647
long long	8字节	-2^63 ~ 2^63-1

当我们加减乘除要运算的数超过数据存储的范围时就无法进行运算，否则会导致越界造成严重的后果，那我们如果要进行这样高精度的计算，就需要使用到算法来对其进行实现，这种算法也可称为高精度算法，能实现高精度的运算；

1 高精度算法的介绍以及思路

当我们由于储存范围的原因无法使用C++的内置类型来进行运算时，我们可以借助STL库中的string来得到要计算的数据，再将string中的数据存入一个数组中，然后对数组中的每一位进行相应的运算，最后的结果存入数组中进行输出，我们的高精度算法也就完成了；

算法思路：

2 高精度加法

对于高精度加法，我们在处理完数据逆序存储于字符串中之后，对每一位进行加法运算，随后处理好进位，如下：

我们先定义一个全局变量，当做数组的大小，该全局变用户可根据需要自行改变，确保其能存下我们需要计算的数据：

const int N = 1e6 + 10;

再定义三个全局数组，分别存储两个要计算的数据和结果

int a[N], b[N], c[N];

然后定义三个全局变量表示三个数据的长度

int la, lb, lc;

先看第一步：将string中要计算的数据，逆序存储于数组中

cin得到要相加的两个数据，并使用string自带的size功能得出三个数据的长度la，lb，lc，结果的长度是两个要加的数据中大的数据的长度，如果说相加到最高位时还有进位，那么lc的长度应为la+1，这种特殊情况后面会单独处理：

string x, y;
cin >> x >> y;

la = x.size(), lb = y.size(), lc = max(la, lb);

如果要让字符串中的数据逆序存储于数组中，即a[0] = x[la - 1 - 0] ; a[1] = x[la -1 - 1] ; a[2] = x[la -1 - 2]; 可以发现，其下标的和正好为la - 1，因此，可以直接得出循环，实现逆序存储：

	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';
	for (int i = 0; i < lb; ++i) b[i] = y[lb - 1 - i] - '0';

这里千万注意，字符串x，y中存储的是字符，当将其转移到数组中时应当减去字符0（‘ 0 ’）；

随后正常执行算法，然后输出，得到基本框架：

	add(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;

下面来实现add算法：

对于数组中的两个数据相加，如下图所示，假设这两个数是1001和9099：

代码实现：

for (int i = 0; i < lc; ++i)
{
	c[i] += a[i] + b[i];
	c[i + 1] = c[i] / 10;
	c[i] %= 10;
}

注意：循环中第一个语句一定是c[i] += a[i] + b[i] ，因为还要算上进位，而第二步即得到进位，进位存储于下一个下标；c[i]本身的值去掉进位后即为c[i] % 10；

在这一步之后还需要更新lc的值，如果在加到最高位之后仍然有进位，那么lc的值应该加1，便于后序输出：

if (c[lc]) ++lc;

由此得到完整的add算法（参数可写可不写，因为是全局的）：

void add(int* a, int* b, int* c)
{
	for (int i = 0; i < lc; ++i)
	{
		c[i] += a[i] + b[i];
		c[i + 1] = c[i] / 10;
		c[i] %= 10;
	}

	if (c[lc]) ++lc;
}

完整代码如下：

#include <iostream>
#include <string>
using namespace std;

const int N = 1e6 + 10;

int a[N], b[N], c[N];

int la, lb, lc;

void add(int* a, int* b, int* c)
{
	for (int i = 0; i < lc; ++i)
	{
		c[i] += a[i] + b[i];
		c[i + 1] = c[i] / 10;
		c[i] %= 10;
	}

	if (c[lc]) ++lc;
}

int main()
{
	string x, y;
	cin >> x >> y;

	la = x.size(), lb = y.size(), lc = max(la, lb);
	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';
	for (int i = 0; i < lb; ++i) b[i] = y[lb - 1 - i] - '0';

	add(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;
}

测试：

3 高精度减法

高精度减法的基本框架和add基本一致，只是在算法的实现上有所区别，先写出其基本框架：

void del(int* a, int* b, int* c)
{
	
}

int main()
{
	string x, y;
	cin >> x >> y;

	la = x.size(), lb = y.size(), lc = max(la, lb);
	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';
	for (int i = 0; i < lb; ++i) b[i] = y[lb - 1 - i] - '0';

	del(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;
}

在此框架的基础上，在将string中的数据拷入数组之前，我们要求x > y，方便后序的减法操作，如果x < y的话，得到的结果应该是一个负数，要先输出符号，然后交换a, b的值；

因此，在进行del之前，应该先比较a，b的值，如下所示：

if (cmp(x, y))
{
	// x < y
	cout << '-';
	swap(x, y);
}

实现cmp：

x，y是两个字符串，我们知道两个字符串比较大小是按照字典序进行比较，也就是说，9会比666666这个字符串还要大，所以我们不能直接使用大小于号进行比较，我们应该先比较其长度，若长度，长度长的，这个数一定更大，长度若相同，则按照字典序进行比较：

bool cmp(string& x, string& y)
{
	if (x.size() != y.size()) return x.size() < y.size();
	return x < y;
}

若x比y小返回真；

再来对del进行实现，del和add有所不同的是，在del的for循环中，a[i]和b[i]要进行相减的运算，这个运算结果暂时存储于c[i]中，如果说c[i] 小于0，说明要向下一位进行借位，那么c[i+1]应当--，同时c[i] 应当 + 10，实现如下：

for (int i = 0; i < lc; ++i)
{
	c[i] += a[i] - b[i];
	if (c[i] < 0)
	{
		--c[i + 1];
		c[i] += 10;
	}
}

在进行了如上循环后，还有一种特殊情况，比如9999 - 9999，按照如上循环得到的c中的结果应该为0000，因为lc的长度没有改变，所以我们需要做进一步处理，在有效数字之前不能存在0，即要去掉前导0，但结果若为0000，还需保留一个0，所以lc的长度至少要为1，如下：

while (lc > 1 && c[lc - 1] == 0) --lc;

完整代码如下：

#include <iostream>
#include <string>
using namespace std;

const int N = 1e6 + 10;

int a[N], b[N], c[N];

int la, lb, lc;

void del(int* a, int* b, int* c)
{
	for (int i = 0; i < lc; ++i)
	{
		c[i] += a[i] - b[i];
		if (c[i] < 0)
		{
			--c[i + 1];
			c[i] += 10;
		}
	}

	while (lc > 1 && c[lc - 1] == 0) --lc;
}

bool cmp(string& x, string& y)
{
	if (x.size() != y.size()) return x.size() < y.size();
	return x < y;
}

int main()
{
	string x, y;
	cin >> x >> y;

	if (cmp(x, y))
	{
		// a < b
		cout << '-';
		swap(x, y);
	}

	la = x.size(), lb = y.size(), lc = max(la, lb);
	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';
	for (int i = 0; i < lb; ++i) b[i] = y[lb - 1 - i] - '0';

	

	del(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;
}

测试：

4 高精度乘法

高精度乘法的基本框架也是和add基本一致，只是在算法的实现上有所区别，先写出其基本框架：

void mul(int* a, int* b, int* c)
{

}

int main()
{
	string x, y;
	cin >> x >> y;

	la = x.size(), lb = y.size(), lc = la + lb;
	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';
	for (int i = 0; i < lb; ++i) b[i] = y[lb - 1 - i] - '0';

	mul(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;
}

这里需要注意的是，lc的大小不再是la和lb较大的那个值，而是la+lb，因为对于两个数相乘，积的长度不会超过两个数的位数之和；

对于高精度乘法，对两个数列竖式计算乘法，如果向我们一般列竖式的做法，整个过程会变得非常麻烦，我们应该采用另一种更简单的方法来列竖式计算———不进制列竖式乘法，即在列竖式时直接写出相乘的结果，在相加后再统一进制，对123×456这两个数进行演示：

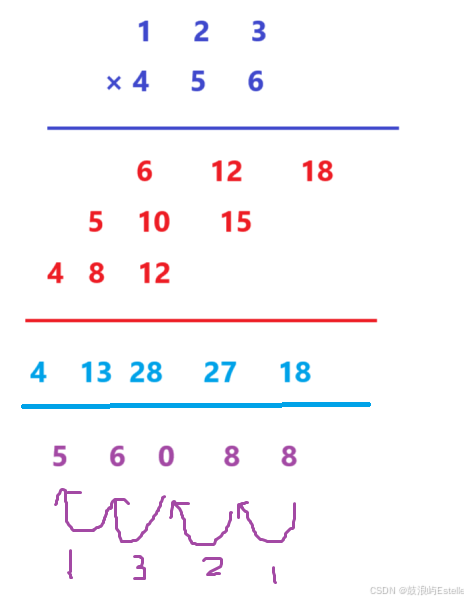
对于a，b和c，有这样的规律 -> a[ i ] * b[ j ]的值刚好是c[ i + j ]处值的叠加，因此，只需要两个for循环就能初步完成这个算法：

for (int i = 0; i < la; ++i)
{
	for (int j = 0; j < lb; ++j)
	{
		c[i + j] += a[i] * b[j];
	}
}

此时得到的c中存储的数据还没有进位，所以我们要对其中的数据进行进位：

	// 进位
	for (int i = 0; i < lc; ++i)
	{
		c[i + 1] += c[i] / 10;
		c[i] %= 10;
	}

同样的，如果是0*9999，得到的结果会是00000，我们还是要处理前导0；

while (lc > 1 && c[lc - 1] == 0) --lc;

完整代码如下所示：

#include <iostream>
#include <string>
using namespace std;

const int N = 1e6 + 10;

int a[N], b[N], c[N];

int la, lb, lc;


void mul(int* a, int* b, int* c)
{
	for (int i = 0; i < la; ++i)
	{
		for (int j = 0; j < lb; ++j)
		{
			c[i + j] += a[i] * b[j];
		}
	}

	// 进位
	for (int i = 0; i < lc; ++i)
	{
		c[i + 1] += c[i] / 10;
		c[i] %= 10;
	}

	while (lc > 1 && c[lc - 1] == 0) --lc;
}

int main()
{
	string x, y;
	cin >> x >> y;

	la = x.size(), lb = y.size(), lc = la + lb;
	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';
	for (int i = 0; i < lb; ++i) b[i] = y[lb - 1 - i] - '0';

	mul(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;
}

测试：

注意，此代码默认输入的两个数为正整数，如果需要计算负数，则在计算之前使用一下绝对值，根据同号为正异号为负的规则先输出符号再正常计算，比较简单，这里不多做演示；

5 高精度除法

对于高精度除法，我一般不研究高精度÷高精度，没什么意义，只需要研究高精度÷低精度足矣，所以其框架会和加减乘有所不同，这里只有被除数需要存储进一个数组，除数则不需要，除出来的结果可能很大，也需要存储进一个数组中；

先写出基本框架：

#include <iostream>
#include <string>
using namespace std;

const int N = 1e6 + 10;

int a[N], b, c[N];

int la, lc;

void sub(int* a, int b, int* c)
{
	
}

int main()
{
	string x;
	cin >> x >> b;

	la = x.size(), lc = la;
	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';

	sub(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;
}

被除数与结果的长度是一样的；

对于sub算法，我们要使用的方法是这样的，以1234 ÷ 45来示范：

sub初步实现如下：

为了使精度的容错更高，余数可能很大，所以我们将t定义为long long类型：

typedef long long LL;

void sub(int* a, int b, int* c)
{
	LL t = 0;
	for (int i = lc - 1; i >= 0; --i)
	{
		t = t * 10 + a[i];
		c[i] = t / b;
		t %= b;
	}
}

同样的，高精度除法也需要去除前导0：

	while (lc > 1 && c[lc - 1] == 0) --lc;

完整代码如下：

#include <iostream>
#include <string>
using namespace std;

const int N = 1e6 + 10;

int a[N], b, c[N];

int la, lc;

typedef long long LL;

void sub(int* a, int b, int* c)
{
	LL t = 0;
	for (int i = lc - 1; i >= 0; --i)
	{
		t = t * 10 + a[i];
		c[i] = t / b;
		t %= b;
	}

	while (lc > 1 && c[lc - 1] == 0) --lc;
}

int main()
{
	string x;
	cin >> x >> b;

	la = x.size(), lc = la;
	for (int i = 0; i < la; ++i) a[i] = x[la - 1 - i] - '0';

	sub(a, b, c);

	for (int i = lc - 1; i >= 0; --i) cout << c[i];
	cout << endl;

	return 0;
}

测试：