链表的环的问题

于 2024-06-04 11:29:02 发布
阅读量749 收藏 14
点赞数 16
文章标签： 链表 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/sysfsv/article/details/138323969
版权

简介

对于链表这一数据结构，它拥有各种类型的结构，我们知道，链表最基本的有三个特征——带头（哨兵位）结点和不带头结点、单向和双向、循环和不循环；

我们仅仅根据这三个基本特征就能将链表的结构分为大致8种情况，链表当然还有很多别的特征，更多的特征对应更多的性质，这也说明着数据结构的多样和灵活性；

那么今天这篇文章，就来向大家介绍一种特殊的链表，它类似于我们的循环链表，却又和循环链表有一定的区别，但在某些局部的性质上又存在着部分联系，难度不大但却有很多有意思的性质，能很好的锻炼我们的代码能力和逻辑思维，它就是带环链表；

1.什么是带环链表？

用一张我们最熟知的单链表和带环链表同时出现的图来向大家解释：

相信通过这张图，大家就能很清楚的初步了解到我们要介绍的带环链表，带环链表和单链表唯一的区别是，单链表的尾结点的指向下一个结点的指针为空，而带环链表的尾结点的指向下一个结点的指针是该链表上的任意一个结点，以此形成了一个类似于环形的结构，因此我们称其为带环结点；

那它和我们早知道的无头单向不循环链表有什么区别呢？单向无头不循环链表的尾结点仅仅指向的是链表的头结点，我们可以将其看做是带环链表的一个特例；

那接下来就向大家简单介绍一下链表的几个环的问题，希望能帮大家更好的理解成环的链表；

2.单链表如何形成带环链表

为了研究带环链表，我们当然需要先创建出一个带环链表，而带环链表是基于单链表实现的，要想创建出一个带环链表，我们需要先创建出一个单链表；

单链表的创建就比较基础的，头插尾插中插，这都能构造出一个单链表，这里我们就用尾插来表示吧，我们直接给出这部分相对基础的代码：

1.申请链表的一个结点pSLNode BuySListNode(SLDataType x)

2.链表尾插数据，void SListPushBack(pSLNode* pphead, SLDataType x)

3.打印出链表，void ShowSList(pSLNode phead)

pSLNode BuySListNode(SLDataType x)
{
	pSLNode newnode = (pSLNode)malloc(sizeof(SLNode));
	if (newnode == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;

	return newnode;
}


void SListPushBack(pSLNode* pphead, SLDataType x)
{
	pSLNode newnode = BuySListNode(x);
	if (*pphead == NULL)
		*pphead = newnode;
	else
	{
		//先找到尾
		pSLNode tail = *pphead;
		while (tail->next)
		{
			tail = tail->next;
		}
		tail->next = newnode;
	}
}


void ShowSList(pSLNode phead)
{
	pSLNode cur = phead;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}

我们可以看看效果：

int main()
{
	//Test1();
	pSLNode plist = NULL;
	int n = 0;
	//输入单链表的值，并以-1结束
	printf("请输入单链表的值，并以-1结束:>\n");
	do
	{
		scanf("%d", &n);
		if (n != -1)
			SListPushBack(&plist, n);
	} while (n != -1);
	ShowSList(plist);

	return 0;
}

这样看来，我们单链表也就构建好了，接下来就是成环的问题；

成环的方法其实很简单，我们只需要找到链表的尾结点，然后让其next指向该链表的任何一个结点就完成了，这里我们不指定尾结点的指向，我们采用随机数的方法，根据链表的长度随机生成环节点，这里就需要我们调用srand和rand函数；

我们要知道一个常识，若我们要生成一个a ~ b的随机数，比如说这个数是k，

那么k = a + rand() % (b - a + 1)；我们一定要将其牢牢记住，那我们根据以上思路来实现这个算法：

void CreateCycle(pSLNode phead, int len)
{
	int k = 0 + rand() % (len - 1 - 0 + 1);
	pSLNode cur = phead;
	while (k--)
	{
		cur = cur->next;
	}
	//找尾
	pSLNode tail = phead;
	while (tail->next)
	{
		tail = tail->next;
	}
	tail->next = cur;
}

len为链表的长度，可在链表插入数据时顺便记录下来；

我们来看看效果（成环成功必然是一个死循环）；

不出所料的一个死循环，可以看到，链表的尾结点指向了倒数第三个结点，成功成环；

3.如何判断链表是否成环

如果我们需要使用到带环链表，那我们就需要提前判断一下该链表是不是一个带环链表，这个问题并不复杂；

我们知道，如果我们安排一个指针依次遍历链表的每个结点，如果该链表带环，那么这个结点就永远走不到NULL，会在这个带环链表中永远循环下去，我们可以通过这个现象来得到判断链表是否带环的思路，那就是我们熟知的快慢指针；

定义两个结点指针slow和fast，slow一次走一步，fast一次走两步，如果链表带环，fast在走到尾之后会返回最初成环的点，如果slow此时已经经过原本成环的结点，fast最终就会追上slow，若slow没有经过原本成环的点，那么fast就会在环上再走一圈继续追赶slow，循环往复，最终fast和slow就会相遇，当fast和slow相遇，我们就能判断出链表确实是带环的；

倘若链表不带环，fast就会先走到NULL或者NULL的前一个结点，意味着我们判断的结果为false；

下面给出一个图示：

我们可以看到，fast走到尾后重新返回了最初成环的结点，追赶slow并与其相遇在了倒数第二个结点，我们由此来进行代码的实现：

bool IsCycle(pSLNode phead)
{
	pSLNode slow = phead;
	pSLNode fast = phead;
	while (fast && fast->next)
	{
		//slow一次走一步
		slow = slow->next;
		//fast一次走两步
		fast = fast->next->next;

		if (fast == slow)
		{
			//相遇了
			return true;
		}
	}

	//fast走到空或链表本身就为空
	return false;
}

我们也可以分装一个函数来判断这个接口的正确性：

void TestIsCycle()
{
	pSLNode plist = NULL;
	printf("请输入单链表的值，并以-1结束:>\n");
	int n = 0;
	do
	{
		scanf("%d", &n);
		if (n != -1)
		{
			SListPushBack(&plist, n);
		}
	} while (n != -1);

	int len = SlistLength(plist);
	CreateCycle(plist, len);

	bool ret = IsCycle(plist);
	if (ret == true)
	{
		printf("该链表是带环链表\n");
	}
	else
	{
		printf("该链表不是带环链表\n");
	}
}

结果展示：

我们再将成环的功能CreateCycle( )屏蔽掉

//int len = SListLength(plist);
//CreateCycle(plist, len);

bool ret = IsCycle(plist);
if (ret == true)
{
	printf("该链表是带环链表\n");
}
else
{
	printf("该链表不是带环链表\n");
}

那我们判断链表是否带环的功能就实现的差不多了，但在实现完这个功能后，我们也会不禁发出一些疑问，为什么slow走一步，fast走两步，它们最后一定会相遇，如果fast一次走3步，4步，5步，这样也是快慢指针，那他们最后也会相遇吗？接下来就让我们来探讨一下：

3.1.判断成环的延伸

我们先来讨论fast走两步的情况下最终一定能和slow相遇，这个问题其实很直观：

如下图所示：

在这个带环链表中，我们知道，slow入环前，fast早已入环，fast在环里走了多少我们无需关注，我们假设，在slow入环后，slow和fast之间的距离是N，那接下来，按照fast每次走两步，slow每次走一步来看；

走一次之后：slow和fast之间的距离：N - 1

走两次之后：slow和fast之间的距离：N - 2

走三次之后：slow和fast之间的距离：N - 3

……

走N次之后：slow和fast之间的距离就会变为0，这就意味着fast一定会追上slow，最终相遇；

————————————————————————————————————————

在看完这个问题之后，我们再来分析分析fast一次走三步的情况，fast还能追上slow吗？还是如上图所示：

每次走完后slow和fast之间的距离就会减少2，那按照这种现象，我们就需要分成两种情况讨论：

当N为奇数和偶数的时候，我们所要面临的就是两种不一样的情况： 

N为奇数N为偶数
走一次距离差N - 2N - 2
走两次距离差N - 4N - 4

走三次距离差

N - 6N - 6
……………………
走N次距离差34
走N+1次距离差12
走N+2次距离差-10

我们可以发现：当N为偶数的时候，走了若干次后，距离差为0，说明fast能追上slow，那当N为奇数时，我们可以看到，走了若干次后，距离差变成了-1、

这个 -1 是什么意思？

这表明，在fast在走三步的情况下，当他们的距离为N时，走了若干次后，fast有可能会反超slow，跑到slow前面，开始新一轮的追赶，如下图所示：

假设环的长度为C，那么在fast反超slow之后，它们之间的距离就变成了C - 1，这样就会展开新一轮的追赶，对于这新一轮追赶fast是否能追上slow，我们又要分两种情况讨论，也就是C-1分别为奇数和偶数的情况：

C - 1为奇数C - 1为偶数
走一次距离差C - 3

C - 3

走两次距离差C - 5  C - 5
走三次距离差C - 7C - 7
……………………
走N回距离差54
走N + 1回距离差12
走N + 2回距离差-10

我们可以看到，在这新一轮追赶中，如果C - 1是偶数，fast就会在新一轮追赶中追赶上slow，若C-1是奇数，经过若干次追赶后，fast和slow之间的距离又会变成-1，即C - 1，距离差又是一个奇数，陷入死循环；

也就是说，在N为奇数的前提下，当C是偶数，C - 1为奇数时，fast永远都不可能追上slow，会一直错过，陷入死循环；

——————————————————————————————————————————

综上所述：

当slow进环时，fast和slow之间的距离为N，N为奇数，同时环的长度C为偶数时，fast走三步，slow走一步，fast永远都不会追上slow；

这是我们理论分析所得出的结论，我们也在潜意识上默认它的正确性；

但是，事实真的如此吗？

C为偶数，同时N为奇数的情况真的会同时存在吗？

结果其实是否定的，这两种情况事实上不可能同时存在，当然这需要我们进一步的分析，我们可以采用反证法，如下图所示：

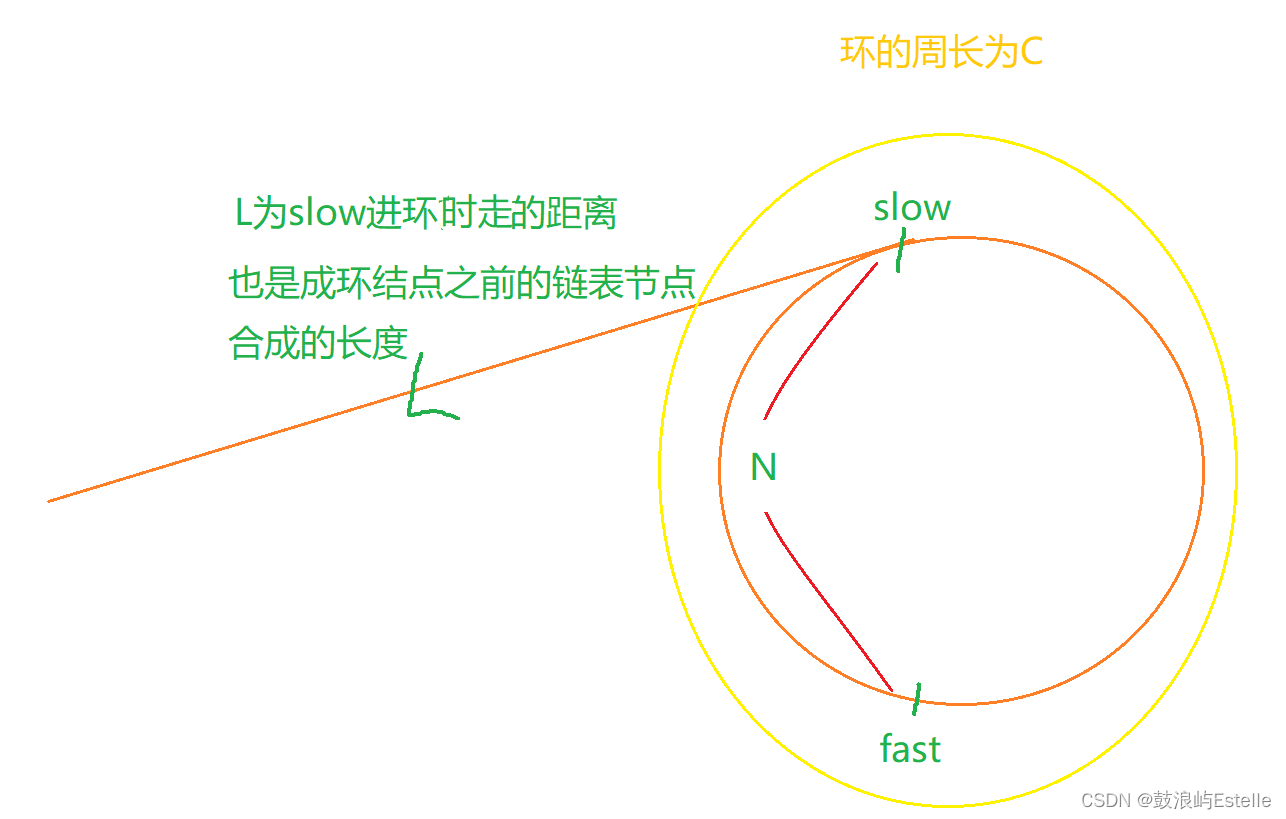
 我们设slow在进环时走过的长度为L，环的周长为C，此时fast和slow之间的距离为N

fast在slow进环前早已进环，或许fast在环内已经走了很多圈，我们假设fast在环内已经走了k圈，k可为0，那fast走过的距离即为L + k * C + C - N；

同时fast行进的距离是slow的三倍，所以fast走过的距离也可以表示为3L；

由此得到如下等式：

3L = L + k * C + C - N；

整理可得：

2L = （k + 1）* C - N;

如果按我们所希望的，N是奇数，同时C是偶数，我们就会得到如下关系：

一个偶数和奇数的差不可能会是一个偶数，因此N为奇数，C为偶数的情况是不可能同时成立的；

要么C、N同为奇数，要么同为偶数，要么N为偶数，C为奇数；

——————————————————————————————————

所以，就算fast走3步，slow走一步，最后也会追上的，第一趟无法追上，在第二趟也一定会追上，这个证明题的坑很深，所以我们一定要注意；

至于fast每走四步、五步等情况，其大致思路和每走三步是一样的，只是在一些细节上分析的更加微妙，这需要我们分更多的情况讨论，这里就不在赘述了，我们来进入下一个模块；

4.如何找到成环的结点；

在研究带环链表的时候，我们也需要知道究竟是那个结点成环；

对于这个问题，我们还是回到fast走两步，slow走一步来解决，在这种情况下，slow和fast从头结点开始往后走，最终会在环上的某一个结点相遇；

我们让一个指针从相遇的节点开始走，另一个结点从头结点开始走，它们最终会在成环结点处相遇；

这个结论的证明，其实也很简单，如下图所示：

我们还是借用这张图，当slow和fast相遇后：

假设相遇的位置距离slow的初始位置为D

此时，slow走过的距离：L + C - D

此时，fast走过的距离：L + k * C + C - D

同时，fast走过的距离也为 ：2 *（L + C - D）

得到如下等式：

2 * ( L + C - D) = L + k * C + C - D

整理可得：

L = D + k * C

这样就能得出这个结论；当一个指针从相遇点开始走时，走过D距离后，再走k圈，k >= 0，其大小就正好为L，与从头结点开始走的结点相遇；

来看代码实现：

pSLNode CycleSList(pSLNode phead)
{
	pSLNode fast = phead, slow = phead;
	while (fast && fast->next)
	{
		slow = slow->next;
		fast = fast->next->next;
		if (slow == fast)
		{
			pSLNode meet = slow;
			pSLNode cur = phead;
			while (meet != cur)
			{
				meet = meet->next;
				cur = cur->next;
			}
			return meet;
		}
	}

	//没找到
	return NULL;
}

那关于链表的环的问题到这也就结束了，这对于我们思维逻辑的训练有很大的帮助，大家也一定要勤动手来手撕代码，多写才能多记忆，才能有更深的体会；下面给出本次博客所写的代码：

代码：

SList.h：

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <time.h>

typedef int SLDataType;

//定义链表的一个结点
typedef struct SListNode
{
	SLDataType data;
	struct SListNode* next;
}SLNode,* pSLNode;

//申请链表的一个节点
pSLNode BuySListNode(SLDataType x);

//尾插数据
void SListPushBack(pSLNode* pphead, SLDataType x);

//打印链表
void ShowSList(pSLNode phead);

//求链表的长度
int SListLength(pSLNode phead);

//成环
void CreateCycle(pSLNode phead, int len);

//判断链表是否成环
bool IsCycle(pSLNode phead);

//求环节点
pSLNode CycleSList(pSLNode phead);

SList.c：

#define  _CRT_SECURE_NO_WARNINGS 1

#include "SList.h"

pSLNode BuySListNode(SLDataType x)
{
	pSLNode newnode = (pSLNode)malloc(sizeof(SLNode));
	if (newnode == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;

	return newnode;
}


void SListPushBack(pSLNode* pphead, SLDataType x)
{
	pSLNode newnode = BuySListNode(x);
	if (*pphead == NULL)
		*pphead = newnode;
	else
	{
		//先找到尾
		pSLNode tail = *pphead;
		while (tail->next)
		{
			tail = tail->next;
		}
		tail->next = newnode;
	}
}


void ShowSList(pSLNode phead)
{
	pSLNode cur = phead;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}


int SListLength(pSLNode phead)
{
	int len = 0;
	pSLNode cur = phead;
	while (cur)
	{
		++len;
		cur = cur->next;
	}

	return len;
}


void CreateCycle(pSLNode phead, int len)
{
	int k = 0 + rand() % (len - 1 - 0 + 1);
	pSLNode cur = phead;
	while (k--)
	{
		cur = cur->next;
	}
	//找尾
	pSLNode tail = phead;
	while (tail->next)
	{
		tail = tail->next;
	}
	tail->next = cur;
}


bool IsCycle(pSLNode phead)
{
	pSLNode slow = phead;
	pSLNode fast = phead;
	while (fast && fast->next)
	{
		//slow一次走一步
		slow = slow->next;
		//fast一次走两步
		fast = fast->next->next;

		if (fast == slow)
		{
			//相遇了
			return true;
		}
	}

	//fast走到空或链表本身就为空
	return false;
}


pSLNode CycleSList(pSLNode phead)
{
	pSLNode fast = phead, slow = phead;
	while (fast && fast->next)
	{
		slow = slow->next;
		fast = fast->next->next;
		if (slow == fast)
		{
			pSLNode meet = slow;
			pSLNode cur = phead;
			while (meet != cur)
			{
				meet = meet->next;
				cur = cur->next;
			}
			return meet;
		}
	}

	//没找到
	return NULL;
}

Test.c：

#define  _CRT_SECURE_NO_WARNINGS 1

#include "SList.h"

void Test1()
{
	pSLNode plist = NULL;
	SListPushBack(&plist, 1);
	SListPushBack(&plist, 2);
	SListPushBack(&plist, 3);
	SListPushBack(&plist, 4);
	SListPushBack(&plist, 5);
	SListPushBack(&plist, 6);
	ShowSList(plist);

}

void TestCreateCycle()
{
	pSLNode plist = NULL;
	int n = 0;
	//输入单链表的值，并以-1结束
	int len = 0;//记录链表的长度
	printf("请输入单链表的值，并以-1结束:>\n");
	do
	{
		scanf("%d", &n);
		if (n != -1)
		{
			SListPushBack(&plist, n);
			++len;
		}
	} while (n != -1);
	ShowSList(plist);

	srand((unsigned int)time(NULL));
	CreateCycle(plist, len);
	printf("成环后的链表为:>\n");
	ShowSList(plist);
}

void TestIsCycle()
{
	pSLNode plist = NULL;
	printf("请输入单链表的值，并以-1结束:>\n");
	int n = 0;
	do
	{
		scanf("%d", &n);
		if (n != -1)
		{
			SListPushBack(&plist, n);
		}
	} while (n != -1);

	int len = SListLength(plist);
	//CreateCycle(plist, len);

	bool ret = IsCycle(plist);
	if (ret == true)
	{
		printf("该链表是带环链表\n");
	}
	else
	{
		printf("该链表不是带环链表\n");
	}
}

int main()
{
	//Test1();
	//TestCreateCycle();
	TestIsCycle();

	return 0;
}

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值