HDU 3903 Trigonometric Function (三角恒等式&余弦定理)_三角恒等式包括余弦定理吗-优快云博客

本文链接：https://blog.youkuaiyun.com/synapse7/article/details/20838077

http://acm.hdu.edu.cn/showproblem.php?pid=3903

如何判断的有理性？

由这三个式子：

$\cos(\theta\pm\psi)=\cos\theta\cos\psi\mp\sin\theta\sin\psi\,$

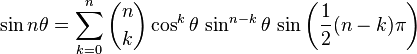
$\sin n\theta = \sum_{k=0}^n \binom{n}{k} \cos^k \theta\,\sin^{n-k} \theta\,\sin\left(\frac{1}{2}(n-k)\pi\right)$

$\cos n\theta = \sum_{k=0}^n \binom{n}{k} \cos^k \theta\,\sin^{n-k} \theta\,\cos\left(\frac{1}{2}(n-k)\pi\right)$

问题可化归为判断A,B,C的正弦和余弦是否为有理数，又由余弦定理

$\angle A = \arccos \frac{{b^2 + c^2 - a^2 }}{{2bc}}\,\!$

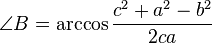
$\angle B = \arccos \frac{{c^2 + a^2 - b^2 }}{{2ca}}\,\!$

$\angle C = \arccos \frac{{a^2 + b^2 - c^2 }}{{2ab}}\,\!$

以及

cos(arccos x)=x

$\sin ( \arccos x)=\sqrt{1-x^2} \,$

若x=p/q，则sqrt(1-x^2)=sqrt(q^2-p^2)/q

故只需判断q^2-p^2是否为完全平方数即可。

完整代码：

/*281ms,356KB*/

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

int main()
{
	int icase;
	scanf("%d", &icase);
	__int64 a, b, c, n, m, k;
	while (icase--)
	{
		cin >> a >> b >> c >> n >> m >> k;
		__int64 d = 4 * b * b * c * c - (b * b + c * c - a * a) * (b * b + c * c - a * a);
		__int64 e = 4 * b * b * a * a - (a * a + b * b - c * c) * (a * a + b * b - c * c);
		__int64 f = 4 * a * a * c * c - (a * a + c * c - b * b) * (a * a + c * c - b * b);
		__int64 x, y, z;
		x = sqrt(d);
		y = sqrt(e);
		z = sqrt(f);
		if (x * x == d && y * y == e && z * z == f) puts("YES");
		else puts("NO");
	}
}