十月每日打卡

每日打卡

10.1 [重新格式化电话号码 lc1694](1694. 重新格式化电话号码 - 力扣（LeetCode）)

模拟题：特殊情况就是在最后划分完全部三个之后，还剩四个需要变成aa-bb

class Solution {
public:
    string reformatNumber(string number) {
        string ans;
        queue<char> q;
        for(char ch: number)
        {
            if(ch != ' ' && ch != '-')
                q.push(ch);
        }
        int cnt = 0;
        while(q.size())
        {
            if(cnt == 0 && q.size() == 4)
            {
                ans += q.front();
                q.pop();
                ans += q.front();
                q.pop();
                ans += '-';
                ans += q.front();
                q.pop();
                ans += q.front();
                q.pop();
            }
            if(!q.size())
                break;
            if(cnt == 3)
            {
                ans += '-';
                cnt = 0;
            }
            else
            {
                ans += q.front();
                q.pop();
                cnt++;
            }
        }
        return ans;
    }
};

10.2 [在LR字符串中交换相邻字符 lc 777](777. 在LR字符串中交换相邻字符 - 力扣（LeetCode）)

题目的意思是L可以越过X向左移动，R可以越过X向右移动。但R和L的相对位置不变。

• ！也就是去掉X后start和end字符串的L和R位置相同！

• R只能右移，L只能左移，所以如果R左边的X多了是不可以的，因为R不能左移过去；同理，L右边的X多了也不可。

class Solution {
public:
    bool canTransform(string start, string end) {
        int n = start.size();
        int i = 0, j = 0;
        while(1)
        {
            //越过所有的X
            while(i < n && start[i] == 'X')
                i++;
            while(j < n && end[j] == 'X')
                j++;
            //判断现在的i和j情况
            //如果两个都走到底了那可以
            if(i == n && j == n)
                return true;
            //有一个走到底了另一个没有或者二者对应的不相同那不行
            if(i == n || j == n || start[i] != end[j])
                return false;
            //两者的位置不同也不行L可以左移所以start的可以在end后面
            if(start[i] == 'L' && i < j)
                return false;
            //R可以右移所以start的可以在end前面
            if(start[i] =='R' && i > j)
                return false;
            i++;
            j++;
        }
        return true;
    }
};

10.2 [每日温度 lc739](739. 每日温度 - 力扣（LeetCode）)

单调栈

单调栈模板题。

就是说维持这个栈单调递减，违反单调性的时候就是需要调整并记录。

如果出现比栈顶大的元素，说明下一个更高温度已经出现，可以将其pop出来了。

如果比栈顶元素小，那么就放在栈里，等待更新最大元素

最终留在栈里的就是没有右边最大元素了，按照初始化的0即可

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temp) {
        int n = temp.size();
        vector<int> ans(n, 0);
        stack<int> stk;
        for(int i = 1; i < n; i++)
        {
            while(!stk.empty() && temp[stk.top()] < temp[i])
            {
                ans[stk.top()] = i - stk.top();
                stk.pop();
            }
            stk.push(i);
        }
        return ans;
    }
};

10.3 [检查二进制字符串字段 lc1784](1784. 检查二进制字符串字段 - 力扣（LeetCode）)

题目含义很难理解，看了评论区之后：连续若干个"1"组成的字段是由一个或者多个连续‘1’组成的，如果这样的字段不超过1个，就返回true，多于1个就返回false。

1000 true 110001 false 统计即可

class Solution {
public:
    bool checkOnesSegment(string s) {
        int cnt = 0;
        int n = s.size();
        int len = 0;
        for(int i = 0; i < n; i++)
        {
            while(i < n && s[i] == '1')
            {
                len++;
                i++;
            }
            if(len >= 1)
                cnt++;
            if(i < n && s[i] == '0')
                len = 0;
            
        }
        return cnt <= 1;
    }
};

10.3 [柱状图中的最大矩形 lc 84](84. 柱状图中最大的矩形 - 力扣（LeetCode）)

我们之前做过一个类似的，盛最多水的容器，那个是构造的矩形是两个边界中最小即可，也即是双指针就行。这个不一样的是你需要使用整个容器内的最矮的作为高。所以我们想遍历每个柱子，以其作为高h，然后去寻找最宽的边，也即是向两边分别找高于h的柱子，找到第一个低于h的就停止。

这个也是单调栈，对于单调递增的栈来说：栈里的前一个元素就是左边第一个小于该元素的值，右边第一个小于我们可以在比较中得到。当发现小于栈顶元素时就可以得到右边第一个了，否则就加入栈中即可。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size() + 2;
        //向两边加一个哨兵
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        int ans = 0;
        stack<int> s;
        for(int i = 0; i < n; i++)
        {
            while(!s.empty() && heights[i] < heights[s.top()])
            {
                int j = s.top();
                s.pop();
                ans = max(ans, heights[j] * (i - s.top() - 1));
            }
            s.push(i);
        }
        return ans;
    }
};

10.3 [最大矩形 lc85](85. 最大矩形 - 力扣（LeetCode）)

就是上面lc84的二维版本

最形象的图就是这个

只用第一行高度是 1 0 1 0 0

12行高度是 2 0 2 1 1

13行高度是 3 1 3 2 2

这几行分别调用lc84即可取最大即可！

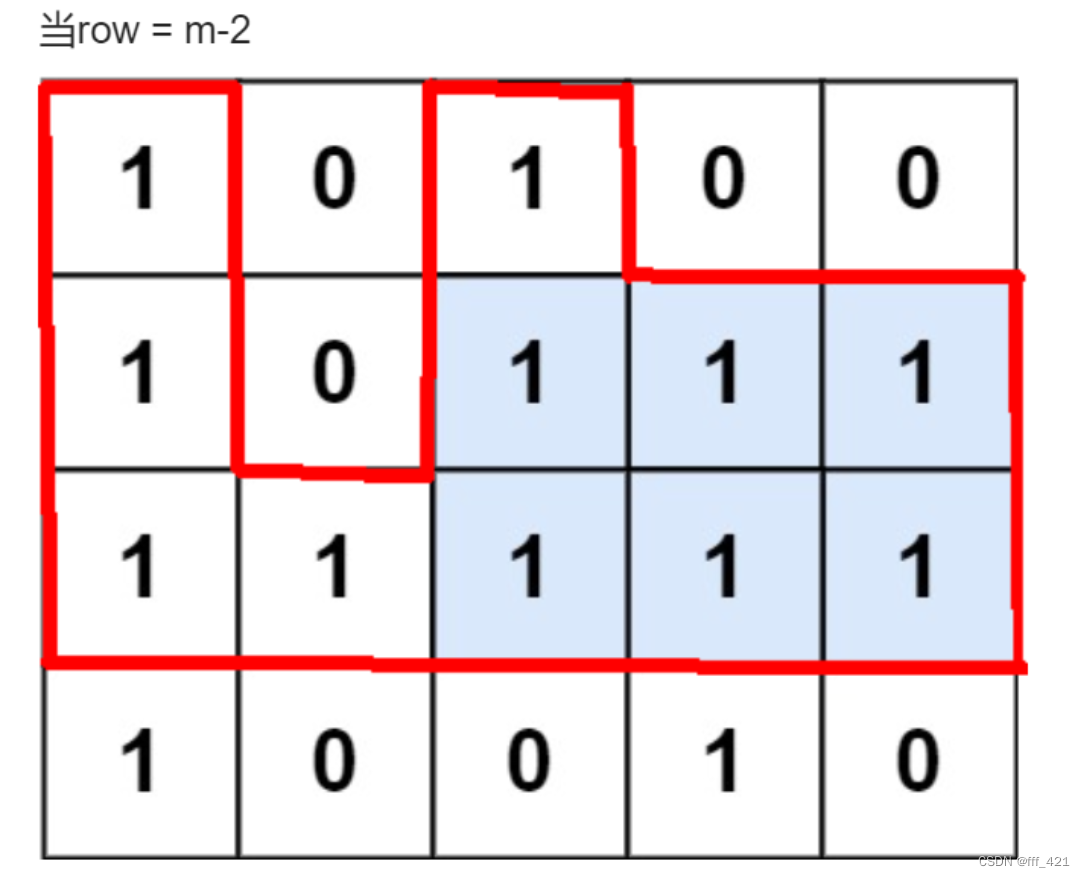
class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int row = matrix.size(), col = matrix[0].size();
        if(row == 0 || col == 0)
            return 0;
        int ans = 0;
        vector<int> height(col, 0);
        for(int i = 0; i < row; i++)
        {
            for(int j = 0; j < col; j++)
            {
                if(matrix[i][j] == '1')
                    height[j] =  height[j] + 1;
                else
                    height[j] = 0;
            }
            for(int x: height)
                cout << x << " ";
            cout << endl;
            ans = max(ans, largestRectangleArea(height));
        }
        return ans;
    }

    int largestRectangleArea(vector<int> heights) {
        int n = heights.size() + 2;
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        int ans = 0;
        stack<int> s;
        for(int i = 0; i < n; i++)
        {
            while(!s.empty() && heights[i] < heights[s.top()])
            {
                int j = s.top();
                s.pop();
                ans = max(ans, heights[j] * (i - s.top() - 1));
            }
            s.push(i);
        }
        return ans;
    }
};

10.4 [使括号有效的最少添加 lc 921](921. 使括号有效的最少添加 - 力扣（LeetCode）)

这个就是有效的括号，但是由于是任意位置插入左括号和右括号都行，只需要数量对应上即可。左括号+1，右括号先抵消再计数即可

class Solution {
public:
    int minAddToMakeValid(string s) {
        int l = 0, cnt = 0;
        for(char ch: s)
        {
            if(ch == '(')
                l++;
            else if(l > 0 && ch == ')')
                l--;
            else if(l == 0 && ch == ')')
                cnt++;
        }
        return cnt + l;
    }
};

10.4 [最短无序连续子数组 lc 581] (581. 最短无序连续子数组 - 力扣（LeetCode）)

这个看起来很简单，本来想着从两边向中间扩展出现无序就停止来着，但是其中的等号很麻烦。这个题一点都不简单。

两个边界l, r。l是最左边需要开始排序的数，应该从右边开始遍历。如果不需要排序的话，那么从右边开始应该每一个数nums[j]都小于等于右边遍历过的min。反之若nums[j] > min的话，就需要记录下来需要排序的值l。

同理，r是最右边需要开始排序的数，应该从左边开始遍历。如果不需要排序的话，那么从左边开始应该每一个数nums[i]都大于等于左边遍历过前i - 1个数的max。反之若nums[j] < max的话，就需要记录下来需要排序的值r。

class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int n = nums.size();
        int ma = INT_MIN, mi = INT_MAX;
        int l = 0, r = 0;
        for(int i = 0; i < n; i++)
        {
            if(nums[i] < ma)
                r = i;
            else
                ma = max(ma, nums[i]);
        }
        for(int j = n - 1; j >= 0; j--)
        {
            if(nums[j] > mi)
                l = j;
            else
                mi = min(mi, nums[j]);
        } 
        if(l == r)
            return 0;
        else
            return r - l + 1;
    }
};

10.5 [子域名访问计数 lc 811](811. 子域名访问计数 - 力扣（LeetCode）)

简单模拟：使用hashmap的key存储域名，value存储个数，处理字符串计数即可。

class Solution {
public:
    vector<string> subdomainVisits(vector<string>& cpdomains) {
        unordered_map<string, int> hashMap;
        vector<string> ans;
        for(string s: cpdomains)
        {
            int i = 0;
            while(i < s.size() && s[i] != ' ')
                i++;
            int cnt = atoi(s.substr(0, i).c_str());
            string s1 = s.substr(++i);  //google.mail.com
            if(hashMap.find(s1) != hashMap.end())
                hashMap[s1] += cnt;
            else
                hashMap[s1] = cnt;
            while(i < s.size() && s[i] != '.')
                i++;
            string s2 = s.substr(++i); //mail.com
            if(hashMap.find(s2) != hashMap.end())
                hashMap[s2] += cnt;
            else
                hashMap[s2] = cnt;
            while(i < s.size() && s[i] != '.')
                i++;
            if(i < s.size() && s[i] == '.')
            {
                string s3 = s.substr(++i); //com
                if(hashMap.find(s3) != hashMap.end())
                    hashMap[s3] += cnt;
                else
                    hashMap[s3] = cnt;
            }
        }
        for(auto x: hashMap)
        {
            string s = to_string(x.second) + " " + x.first;
            ans.push_back(s);
        }
        return ans;
    }
};

[10.5 盛最多水的容器 lc 11](11. 盛最多水的容器 - 力扣（LeetCode）)

这个就很简单啦，双指针遍历一下

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int i = 0, j = n - 1;
        int ans = 0;
        while(i < j)
        {
            int s = min(height[i], height[j]) * (j - i);
            ans = max(ans, s);
            if(height[i] < height[j])
                i++;
            else
                j--;
        }
        return ans;
    }
};

[10.5 删掉链表的倒数第n个节点 lc 19](19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）)

也很简单啦，就是快慢指针先找到倒数第n个节点，然后删除即可。

注意一些边界条件，比如删除头节点、删除只有一个元素的链表等

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* p = head;
        if(head->next == nullptr)
            return nullptr;
        for(int i = 0; i < n; i++)
            p = p->next;
        ListNode* q = head;
        if(p == nullptr)
            return head->next;  //删掉头节点

        while(p->next != nullptr)
        {
            p = p->next;
            q = q->next;
        }
        ListNode* nx = q->next;
        q->next = nx->next; 
        return head;
    }
};

[10.6 三等分 lc 927](927. 三等分 - 力扣（LeetCode）)

三个指针判断三部分是否相等，二进制是否相等首先看1的个数，其次看第一个1后的排列是否相等。`

class Solution {
public:
    vector<int> threeEqualParts(vector<int>& arr) {
        vector<int> ans = {-1, -1};
        int n = arr.size();
        int cnt = 0;
        //求出所有1的数量
        for(int i = 0; i < n; i++)
            cnt += arr[i];
        if(cnt == 0)
            return {0, n - 1};
        //三者平分 能分继续 不能分就不行
        if(cnt % 3) return ans;
        cnt = cnt / 3;
        int i = 0, j = 0, k = 0, s = 0;
        //根据1的数量将三个指针定位到各自第一个1的位置
        while(i < n && s < 1) { s += arr[i++];}
        s = 0;
        while(j < n && s < cnt + 1)  { s += arr[j++];}
        s = 0;
        while(k < n && s < 2 * cnt + 1)  { s += arr[k++];}

        //开始判断第一个1后面的是否完全相同
        while(k < n && arr[i] == arr[j] && arr[j] == arr[k])
        {
            i++; j++; k++;
        }
        if(k < n)
            return ans;
        else
            return {i - 1, j};

    }
};

[10.6 下一个排列 lc 31](31. 下一个排列 - 力扣（LeetCode）)

这个题挺巧妙的，需要仔细分析排列。我们以2 6 3 5 4 1为例，可以从右边开始分析。就是如果是降序比如5 4 1这样的，就是已经是最大的了，不会再有下一个排列了。所以我们第一步需要从右边找第一个升序的，找到了 3 5。为了是下一个排列因此我们需要使这个排列尽可能地小，所以我们从后面5 4 1中选一个第一个比3大地和他交换，得到一个比3大一点的新开头，2 6 4 5 3 1。接下来需要将后面的变成最小的，因为是逆序，所以直接反转即可。

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int n = nums.size();
        int i = n - 1;
        //找到第一个升序的 3 5 
        while(i > 0 && nums[i] <= nums[i - 1]) i--;
        //如果不存在升序说明全部倒序，直接全部逆序即可
        if(i <= 0) {reverse(nums.begin(), nums.end()); return;}
        int j = i - 1; // j是3 等着待交换的那个
        //向右边倒序序列中找比nums[j]大一点的值 i - 1就是那个4
        while(i < n && nums[i] > nums[j]) i++;
        cout << nums[j] << " " << nums[i - 1] << endl;
        //swap(nums[j], nums[i - 1]); 将二者交换
        int t = nums[j];
        nums[j] = nums[i - 1];
        nums[i - 1] = t;
        //最后将后面的倒序逆转变小一点的排列
        reverse(nums.begin() + j + 1, nums.end());
    }
};

单调栈版本 等价于lc 556

class Solution {
public:
    //nums是有n数字分割来的,所以是倒序的
    int nextGreaterElement(vector<int> nums) {
        stack<int> stk;
        int x = -1, y = -1;
        for(int i = 0; i < nums.size(); i++)
        {
            if(stk.size() && nums[i] < nums[stk.top()])
            {
                x = i;
                while(stk.size() && nums[i] < nums[stk.top()])
                {
                    y = stk.top();
                    stk.pop();
                }
                swap(nums[x], nums[y]);
                reverse(nums.begin(), nums.begin() + x);
                break;
            }
            stk.push(i);  
        }
        if(x == -1) return -1;
        long long ans = 0, k = 1;
        for(int i = 0; i < nums.size(); i++)
        {
            ans += nums[i] * k;
            k = k * 10;
        }
        cout << ans << endl;
        if(ans > INT_MAX) return -1;
        else return ans;
    }
};

[10.7 最大升序子序列和 lc1800](1800. 最大升序子数组和 - 力扣（LeetCode）)

class Solution {
public:
    int maxAscendingSum(vector<int>& nums) {
        int ans = nums[0], s = nums[0];
        for(int i = 1; i < nums.size(); i++)
        {
            if(nums[i - 1] < nums[i])
                s += nums[i];
            else
                s = nums[i];
            ans = max(ans, s);
        }
        return ans;
    }
};

[10.7 寻找重复数 lc 287](287. 寻找重复数 - 力扣（LeetCode）)

快慢指针，将1,3,4,2,2看成链表，判断链表是否有环以及找到链表的入口。

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        //将数组看成链表,找到环的入口
        int slow = 0, fast = 0;
        while(1)
        {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if(slow == fast)
                break;
        }
        fast = 0;
        while(slow != fast)
        {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
};

[10.7 找到数组中消失的数字 lc 448](448. 找到所有数组中消失的数字 - 力扣（LeetCode）)

这个题也是将数组中的值和下标映射起来，比如[4,3,2,7,8,2,3,1]，nums[0] = 4，则将4对应的nums[4] = 8换成-8代表有4了，重复的已经成为负数的就不变，最后值为正的下标就是消失的数字。

class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> ans;
        for(int i = 0; i < nums.size(); i++)
        {
            nums[abs(nums[i]) - 1] = - abs(nums[abs(nums[i]) - 1]);
        }
        for(int i = 0; i < nums.size(); i++)
        {
            if(nums[i] > 0)
                ans.push_back(i + 1);
        }
        return ans;
    }
};

[10.8 优势洗牌 lc 870](870. 优势洗牌 - 力扣（LeetCode）)

贪心之田忌赛马：在nums1中找大于nums2[i]的最小值，如果没有则返回nums1中的最小值。直接找会导致超时，二分查找第一个。

class Solution {
public:
    vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size();
        vector<int> ans(n, 0);
        bool st[n];
        int idx = 0;
        memset(st, false, sizeof st);
        sort(nums1.begin(), nums1.end());
        for(int i = 0; i < n; i++)
        {
            int l = 0, r = n;
            while(l < r)
            {
                int mid = l + r >> 1;
                if(nums1[mid] > nums2[i])
                    r = mid;
                else
                    l = mid + 1;
            }
            while(l < n && (st[l] || nums1[l] == nums2[i]))
                l++;
            if(l < n)
            {
                ans[i] = nums1[l];
                st[l] = true;
            }
            else
            {
                while(st[idx]) idx++;
                ans[i] = nums1[idx];
                st[idx++] = true;
            }
       }
        return ans; 
    }
};

10.8 三数之和 lc 15

排序的两数之和的变形 lc 167：如果一个数组已经排序了求两数之和那么可以使用双指针，一个从0开始，一个从n - 1开始，如果和大于sum那么j–，小于sum那么i++；

这道题：他说顺序不重要，我们可以按照i < j < k的顺序返回

还要去除重复就是如果i j k在遇到和上一个一样的时候要跳过。

两个优化：

• 如果nums[i]和离他最近的两个（最小的）都 大于0了，那么全部不可能
• 如果nums[i]和离他最远的两个（最大的）都小于0了，那么当前x不可能

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> ans;
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for(int i = 0; i < n - 2; i++)
        {
            if(i > 0 && nums[i] == nums[i - 1])
                continue;
            //优化1:
            if(nums[i] + nums[i + 1] + nums[i + 2] > 0) break;
            //优化2:
            if(nums[i] + nums[n - 2] + nums[n - 1] < 0) continue;
            int j = i + 1, k = n - 1;
            while(j < k)
            {  
                int s = nums[i] + nums[j] + nums[k];
                if(!s) {
                    ans.push_back({nums[i], nums[j], nums[k]});
                    while(j < k && nums[j] == nums[j + 1]) j++;
                    while(j < k && nums[k] == nums[k - 1]) k--;
                    j++; k--;
                }
                else if(s > 0) k--;
                else j++;                                      
            }
        }
        return ans;
    }
};

[10.10 数组中第k个元素](215. 数组中的第K个最大元素 - 力扣（LeetCode）)

1. 快速排序

快速排序每次都可以使nums[r]== x，然后左侧都小于等于x，右侧都大于等于x。因此只要某次确定值的下标是k就可以返回第k个最大的元素了。

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        return quicksort(nums, k, 0, nums.size() - 1);
    }

    int quicksort(vector<int>& nums, int k, int left, int right)
    {
        if(right < left)
            return INT_MAX;
        int x = nums[(left + right) >> 1];
        int l = left - 1, r = right + 1;
        while(l < r)
        {
            do l++; while(nums[l] > x);
            do r--; while(nums[r] < x);
            if(l < r)
            {
                int t = nums[l]; nums[l] = nums[r]; nums[r] = t;
            }
        }
        int p;
        if(nums[l] == x)
            p = l;
        if(nums[r] == x)
            p = r;
        if(p == k - 1)
            return nums[p];
        else if(p > k - 1)
            return quicksort(nums, k, left, r);
        else
            return quicksort(nums, k, r + 1, right);
        
    }
};

2. 建堆

维护一个k长度的大顶堆，堆顶元素就是第k大，当堆顶元素不再是第k大的时候，就调整堆。

最小堆 - 数组中的第K个最大元素 - 力扣（LeetCode）

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int n = nums.size();

        make_heap(nums, k);
        for(int i = k; i < n; i++)
        {
            if(nums[i] < nums[0])
                continue;
            else
            {
                nums[0] = nums[i];
                shift_down(nums, k, 0);
            }
        }
        return nums[0];
    }

    void shift_down(vector<int>& nums, int k, int i)
    {
        int j = 2 * i + 1;
        while(j < k)
        {
            if(j + 1 < k && nums[j] > nums[j + 1]) j++;
            if(nums[i] > nums[j])
            {
                swap(nums[i], nums[j]);
                i = j;
                j = 2 * i + 1;
            }
            else
                break;
        }
    }
    void make_heap(vector<int>& nums, int k)
    {
        for(int i = k / 2; i >= 0; i--)
            shift_down(nums, k, i);
    }
};

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int n = nums.size();

        //构建具有k个元素(nums[0..k-1])的最小堆, 时间复杂度O(nlogk)
        make_heap(nums, k);

        //从数组nums的第k+1个元素(nums[k])开始，依次替换堆顶，然后调整为最小堆
        for (int i = k; i < n; i++) {
            if (nums[i] < nums[0])    //扫描到的元素nums[i]比堆顶元素小，丢弃
                continue;
            nums[0] = nums[i];        //替换堆顶元素
            sift_down(nums, 0, k);    //堆顶元素下沉
        }
        return nums[0];               //堆顶元素即为第k大数
    }
    //将编号为i的结点下沉。时间复杂度：O(logk)
    void sift_down(vector<int> &nums, int i, int k) {
        int j = i * 2 + 1;          //计算结点i的左孩子编号
        while (j < k) {             //结点i有左孩子
            //结点i有右孩子，且右孩子的值小于左孩子
            if (j + 1 < k && nums[j + 1] < nums[j])
                j++;
            if (nums[i] > nums[j]) {    //双亲的值大，应该下沉到孩子结点的位置
                swap(nums[i], nums[j]); //将孩子交换到双亲位置
                i = j;
                j = i * 2 + 1;
            } else break;
        }
    }
    //创建最小堆：O(nlogk)
    void make_heap(vector<int> &nums, int k) {
        //从最后一个非叶子结点开始进行调整（下沉）
        for (int i = k / 2; i >= 0; i--)    //k最大可以取到n(数组长度)
            sift_down(nums, i, k);          //时间复杂度O(logk)
    }
};

int main(int argc, char *argv[])
{
    vector<int> nums = {3, 2, 1, 5, 6, 4};
    int k = 2;

    // vector<int> nums = {3, 2, 3, 1, 2, 4, 5, 5, 6};
    // int k = 4;

    Solution obj;
    int res = obj.findKthLargest(nums, k);
    cout << res << endl;

    return 0;
}

10.10 使序列递增的最小交换次数 lc 801

状态机dp:dp[i] [0]表示第i位不发生交换使得前i位递增的最小交换次数,1同理。

有两种情况可以交换：

• 两组都满足前后大于，这种就是要不i和i-1都不交换，要么都交换。
• 交叉满足前后大小关系，这种要不i- 1交换要不i交换。

class Solution {
public:
    int minSwap(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size();
        int dp[n][2];
        memset(dp, 0x3f, sizeof dp);
        dp[0][0] = 0;
        dp[0][1] = 1;
        for(int i = 1; i < n; i++)
        {
            if(nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1])
            {
                dp[i][0] = dp[i - 1][0];  //要么不交换
                dp[i][1] = dp[i - 1][1] + 1; //要么两个都交换
            }
            if(nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1])
            {
                dp[i][0] = min(dp[i][0], dp[i - 1][1]);  //前一个发生交换
                dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1); //后面这个发生交换
            }
        }
        return min(dp[n - 1][0], dp[n - 1][1]);
    }
};

10.11 仅执行一次字符串交换能否使两个字符串相等 lc 1790

记录下两个不同的下标，超过两个不同返回false，最后看不同的两个下标交换后是否相同。

class Solution {
public:
    bool areAlmostEqual(string s1, string s2) {
        int n = s1.size();
        int cnt = 0;
        int a[2];
        for(int i = 0; i < n; i++)
        {
            if(s1[i] != s2[i])
            {
                if(cnt == 2)
                {
                    cnt++;
                    break;
                }
                a[cnt++] = i;
            }
        }
        if(cnt == 1 || cnt > 2)
            return false;
        if(cnt == 0)
            return true;
        if(s1[a[0]] == s2[a[1]] && s1[a[1]] == s2[a[0]])
            return true;
        return false;
    }
};

10.12 链表组件 lc 817

模拟即可

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
// 被骗了,是求所有组件的个数而不是求组件的最大长度无语无语
    int numComponents(ListNode* head, vector<int>& nums) {
        int n = nums.size(), ans = 0;
        unordered_set<int> hashset;
        for(int x: nums)
            hashset.insert(x);
        ListNode* p = head;
        int cnt = 0;
        while(p != nullptr)
        {
            if(hashset.find(p->val) != hashset.end())
                cnt++;
            else
            {
                if(cnt)
                    ans++;
                cnt = 0;
                
            }
            p = p->next;
        }
        if(cnt)
            ans++;
        return ans;
    }
};

10.12 接雨水 lc 42

接雨水的关键就是单调栈

不同于柱状图的最大矩形（向两边找低于栈顶的递增），接雨水需要向两边找高于栈顶的，这样才能接住雨水，因此是递减栈。

以栈顶元素作为雨水高度t = height[stk.top()]，当右边高于栈顶时，就是找到了右边高于的，然后去找左边高于的，也即是下一个栈顶。还有要是有和栈顶相同的也要pop出去，而且高度要减去。下一个栈顶就是左边高于栈顶的了height[stk.top()]。比较这两边高的选小的作为高，减去t，乘上宽度即可。

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        int ans = 0;
        stack<int> stk;
        for(int i = 0; i < n; i++)
        {
            while(!stk.empty() && height[i] > height[stk.top()])
            {
                int t = stk.top();
                stk.pop();
                while(!stk.empty() && height[stk.top()] == height[t])
                    stk.pop();
                if(!stk.empty())
                    ans += ( min(height[stk.top()], height[i]) - height[t] ) * (i - stk.top() - 1);
            }
            stk.push(i);
        }
        return ans;
    }
};

10.13 合并K个升序链表 lc 23

两两归并，最后变成两个合并。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2)
    {
        ListNode* dummy = new ListNode(-1);
        ListNode* p = dummy;
        if(l1 == nullptr && l2 == nullptr)
            return nullptr;
        while(l1 != nullptr && l2 != nullptr)
        {
            if(l1->val < l2->val)
            {
                p->next = l1;
                l1 = l1->next;
            }
            else
            {
                p->next = l2;
                l2 = l2->next;
            }
            p = p->next;
        }
        while(l1 != nullptr)
        {
            p->next = l1;
            l1 = l1->next;
            p = p->next;
        }
        while(l2 != nullptr)
        {
            p->next = l2;
            l2 = l2->next;
            p = p->next;
        }
        return dummy->next;
    }
    ListNode* binaryMerge(vector<ListNode*>& lists, int low, int high)
    {
        if(low > high)
            return nullptr;
        if(low == high)
            return lists[low];
        if(high - low == 1)
            return mergeTwoLists(lists[low], lists[high]);
        int mid = (low + high) >> 1;
        return mergeTwoLists(binaryMerge(lists, low, mid), binaryMerge(lists, mid + 1, high));
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return binaryMerge(lists, 0, lists.size() - 1);
    }
};

10.13 找到字符串中所有字母异位词 lc 438

滑动窗口

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        vector<int> ans;
        int sn = s.size();
        int pn = p.size();
        if(pn > sn) return {};
        int cnts[26];
        int cntp[26];
        memset(cnts, 0, sizeof cnts);
        memset(cntp, 0, sizeof cntp);
        for(int i = 0; i < pn; i++)
            cntp[p[i] - 'a']++;
        int i = 0, j = 0;
        for(; j < pn; j++)
            cnts[s[j] - 'a']++;
        while(j < sn)
        {
            bool f = true;
            for(int k = 0; k < 26; k++)
            {
                if(cnts[k] != cntp[k])
                    f = false;
            }
            if(f)
                ans.push_back(i);
            cnts[s[i++] - 'a']--;
            if(j < sn)
                cnts[s[j++] - 'a']++;  
        }
        bool f = true;
        for(int k = 0; k < 26; k++)
        {
            if(cnts[k] != cntp[k])
                f = false;
        }
        if(f)
            ans.push_back(i);
        return ans;
    }
};

10.13 最多能完成排序的块 lc 769

规律：区间数的最大值小于等于下标就可以分块

或者统计下标的和等于区块的和也可以分块。

总之就是区块内的元素需要和下标一致。

class Solution {
public:
    int maxChunksToSorted(vector<int>& arr) {
        //区间的最大值小于等于索引则可以划分区间
        int n = arr.size();
        int ans = 0, ma = 0;
        for(int i = 0; i < n; i++)
        {
            if(arr[i] > ma)
                ma = arr[i];
            if(ma <= i)
            {
                ans++;
                ma = 0;
            }
        }
        return ans;
    }
};

10.14 不同的子序列II lc940

题目翻译一下是从s的子序列中选出t的个数

还是不太懂捏（别急，11月的我来再学一遍）

这回彻底明白了

我们对于每个s[i]有在之前情况上再进行选和不选两种情况，首先不选的情况就是上一次s[i - 1]的那些字符串，选就是在s[i - 1]那些字符串上加上a后缀，然后再加上一个以s[i]为单独子序列的字符串。

但是可以造成重复，比如“aba” 前面是 a, b, ab, 我们在选第三个a的时候，把a当作单独子序列时会与不选a时的之前的a重复。

因此我们以是否以s[i]为后缀区分，dp[i] [j]表示使用前i个字符以j为后缀的字符串数量，分两步：

• 不选s[i]：dp[i] [j] = dp[i - 1] [j] //a, b, ab

• 选s[i]，重新计算以s[i]为后缀的字符串数量，这时我们不考虑之前的以s[i]为后缀的，我们仅仅考虑以当前s[i]为后缀，这样就不会导致重复//不考虑a, b, ab中的a

  dp[i] [s[i] - ‘a’] = 1 + (求和, j从1到26)dp[i - 1] [j]

class Solution {
public:
    const int mod = 1e9 + 7;
    int distinctSubseqII(string s) {
        int sn = s.size(), ans = 0;
        int dp[sn][26];
        memset(dp, 0, sizeof dp);
        dp[0][s[0] - 'a'] = 1;
        for(int i = 1; i < sn; i++)
        {
            for(int j = 0; j < 26; j++)
                dp[i][j] = dp[i - 1][j]; //不选s[i],这些以j结尾的字符串数量和s[i - 1]时一样
            
            //下面这段可以换成
            //dp[i][s[i] - 'a'] = accumulate(dp[i], dp[i] + 26, 1L) % mod;
            dp[i][s[i] - 'a'] = 1;  //以s[i]单独为一个字符串
            for(int j = 0; j < 26; j++)
                dp[i][s[i] - 'a'] = ((long long)dp[i][s[i] - 'a'] + dp[i - 1][j]) % mod; //选上s[i], 就是改一下以s[i]结尾的字符串数量
           
        }
        for(int i = 0; i < 26; i++)
            ans = ((long long)ans + dp[sn - 1][i]) % mod;
        return ans;
    }
};

10.14 不同的子序列 I lc 115

class Solution {
public:
    const int mod = 1e9 + 7;
    int numDistinct(string s, string t) {
        int sn = s.size(), tn = t.size();
        int dp[sn + 1][tn + 1];
        //dp[i][j]表示st中使用前i个去匹配t中的前j个用的个数
        memset(dp, 0, sizeof dp);
        for(int i = 0; i <= sn; i++)
            dp[i][0] = 1;
        for(int i = 1; i <= sn; i++)
        {
            for(int j = 1; j <= tn; j++)
            {
                //匹配上了：我们可以选择用不用s[i]去匹配，不用是s[i]是后面可能还有，我们先不用s[i]
                if(s[i - 1] == t[j - 1])
                    dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % mod;
                else
                    dp[i][j] = dp[i - 1][j];
            }
        }
        return dp[sn][tn];
    }
};

10.14 路径总和 I lc 112

我一开始写的是，先不管下面这个空树是否为空。看[1, 2] 1 这个例子，就是这棵树只有1 ，2 一侧两个节点。在我的判断中走到1这个节点就可以判断true了。但是题目要求的是到叶子节点，所以判断条件要加上节点的左右节点都为空。

//wrong
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr && targetsum == 0)
            return true;
        if(root == nullptr)
            return false;
        return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
    }
};

//right
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr)
            return false;
        if(targetSum == root->val && root->left == nullptr && root->right == nullptr)
            return true;
        return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
    }
};

10.14 路径总和II lc 113

在1的基础上要记录下满足要求的路径和

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> tmp;
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if(root == nullptr)
            return {};
        helper(root, targetSum);
        return ans;
    }
    void helper(TreeNode* root, int targetSum)
    {
        if(root == nullptr)
            return;
        if(targetSum == root->val && !root->left && !root->right)
        {
            tmp.push_back(root->val);
            ans.push_back(tmp);
            tmp.pop_back();
            return ;
        }
        tmp.push_back(root->val);
        helper(root->left, targetSum - root->val);
        helper(root->right, targetSum - root->val);
        tmp.pop_back();
    }
};

10.14 路径总和III lc 437

路径不需要从父节点开始，也不需要在叶子节点结束，但方向要向下。

两个dfs，第一个dfs遍历每个节点，第二dfs去计算和是否满足。

class Solution {
public:
    long long  ans = 0;
    int ts;
    int pathSum(TreeNode* root, int targetSum) {
        if(root == nullptr)
            return 0;
        ts = targetSum;
        dfs1(root);
        return ans;
    }
    void dfs1(TreeNode* root)
    {
        if(root == nullptr)
            return;
        dfs2(root, 0);
        dfs1(root->left);
        dfs1(root->right);
    }
    void dfs2(TreeNode* root, long long curSum)
    {
        if(root == nullptr)
            return;
        curSum += root->val;

        if(curSum == ts)
            ans++;
        
        dfs2(root->left, curSum);
        dfs2(root->right, curSum);
    }
};

树上的前缀和：哇塞！最完整的路径是从根节点到叶子节点，这题相当于在这些路径上找区间和=targetsum的，那不就是前缀和吗！

curSum - preSum = targetSum即可。

class Solution {
public:
    unordered_map<long long, int> preSum;
    int targetSum;
    int ans = 0;
    int pathSum(TreeNode* root, int ts) {
        if(root == nullptr)
            return 0;
        targetSum = ts;
        preSum[0] = 1;
        dfs(root, 0);
        return ans;
    }
    void dfs(TreeNode* root, long long curSum)
    {
        if(root == nullptr)
            return;
        curSum += root->val;
        if(preSum.find(curSum - targetSum) != preSum.end())
        {
            ans += preSum[curSum - targetSum];
        }
        preSum[curSum]++;
        dfs(root->left, curSum);
        dfs(root->right, curSum);
        preSum[curSum]--;
    }
};

10.14 二叉树的序列化与反序列化 lc 297

这道题主要是区分每个节点的值和null处理、负值处理的问题，其他就是递归即可

BFS

class Codec {
public:
    const int nll = 2000;
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        if(root == nullptr)
            return "";
        string data;
        queue<TreeNode*> q;
        q.push(root);
        while(q.size())
        {
            TreeNode* tmp = q.front();
            q.pop();
            if(tmp == nullptr)
            {
                data += "_#";
                continue;
            }a
            data += "_" + to_string(tmp->val);
            q.push(tmp->left);
            q.push(tmp->right);
        }
        cout << data << endl;
        return data;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        if(data.size() == 0)
            return nullptr;
        vector<int> v;
        int i = 0;
        while(i < data.size())
        {
            int j = i + 1;
            while(j < data.size() && data[j] != '_')
                j++;
            string s = data.substr(i + 1, j - i - 1);
            cout << s << endl;
            if(s == "#")
                v.push_back(nll);
            else
                v.push_back(atoi(s.c_str()));
            i = j;
        }
        i = 0;
        TreeNode* root = new TreeNode(v[i++]);
        queue<TreeNode*> q;
        q.push(root);
        while(q.size())
        {
            TreeNode* tmp = q.front();
            q.pop();
            if(v[i] == nll)
                tmp->left = nullptr;
            else
            {
                tmp->left = new TreeNode(v[i]);
                q.push(tmp->left);
            }
            i++;
            if(v[i] == nll)
                tmp->right = nullptr;
            else
            {
                tmp->right = new TreeNode(v[i]);
                q.push(tmp->right);
            }
            i++;
        }
        return root;
    }
};

DFS

class Codec {
public:
    const int nll = 2000;
    vector<int> v;
    int i = 1;
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        if(root == nullptr)
            return "_#";
        return "_" + to_string(root->val) +  serialize(root->left) + serialize(root->right);
    }
    void helper(string data)
    {
        int i = 0;
        while(i < data.size())
        {
            int j = i + 1;
            while(j < data.size() && data[j] != '_')
                j++;
            string s = data.substr(i + 1, j - i - 1);
            cout << s << endl;
            if(s == "#")
                v.push_back(nll);
            else
                v.push_back(atoi(s.c_str()));
            i = j;
        }
    }
    TreeNode* build(TreeNode* root)
    {
        if(v[i] == nll)
        {
            root->left = nullptr;
            i++;
        }
        else
        {
            root->left = new TreeNode(v[i]);
            i++;
            build(root->left);
        }
        if(v[i] == nll)
        {
            root->right = nullptr;
            i++;
        }
        else
        {
            root->right = new TreeNode(v[i]);
            i++;
            build(root->right);
        }
        return root;
    }
    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        if(data == "_#")
            return nullptr;
        helper(data);
        TreeNode* root = new TreeNode(v[0]);
        return build(root);
    }
};

10.15 目标和 lc494

1.简单dfs

class Solution {
public:
    int n;
    //int ans = 0;
    int findTargetSumWays(vector<int>& nums, int target) {
        n = nums.size();
        return dfs(nums, target, 0, 0);
    }
    int dfs(vector<int>& nums, int target, int curSum, int i)
    {
        if(i == n && curSum == target)
            return 1;
        if(i == n)
            return 0;
        int n1 = dfs(nums, target, curSum + nums[i], i + 1);
        int n2 = dfs(nums, target, curSum - nums[i], i + 1);
        return n1 + n2;
    }
};

2. dfs+记忆化搜索

memo记录的是key = (i, cursum)， value=要求的个数

class Solution {
public:
    int n;
    //int ans = 0;
    unordered_map<string, int> memo;
    int findTargetSumWays(vector<int>& nums, int target) {
        n = nums.size();
        return dfs(nums, target, 0, 0);
    }
    int dfs(vector<int>& nums, int target, int curSum, int i)
    {
        string key = to_string(i) + "_" + to_string(curSum);
        if(memo.count(key))
            return memo[key];
        if(i == n && curSum == target)
        {
            memo[key]++;
            return memo[key];
        }
        if(i == n)
        {
            memo[key] = 0;
            return memo[key];
        }
        int n1 = dfs(nums, target, curSum + nums[i], i + 1);
        int n2 = dfs(nums, target, curSum - nums[i], i + 1);
        memo[key] = n1 + n2;
        return n1 + n2;
    }
};

3. 01背包

在记忆化的基础上变成01背包

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int n = nums.size();
        int sum = 0;
        for(int x: nums)
            sum += x;
        if(target > sum || target < -sum) return 0;
        vector<vector<int>> dp(n + 1, vector<int>(2 * sum + 1, 0));
        dp[0][0 + sum] = 1;
        for(int i = 1; i <= n; i++)
        {
            for(int cur = -sum; cur <= sum; cur++)
            {
                if(cur - nums[i - 1] >= -sum)
                    dp[i][cur + sum] = dp[i - 1][cur - nums[i - 1] + sum];
                if(cur + nums[i - 1] <= sum)
                    dp[i][cur + sum] += dp[i - 1][cur + nums[i - 1] + sum];
            }
        }
        return dp[n][target + sum];
    }
};

10.15 分割等和子集 lc 416

划分两个子集使得x = y，也即是找到一个子集使得x=sum/2。也就是从这些数字中选一些数使得和为sum/2。

01背包问题

class Solution {
public:
    int n;
    bool canPartition(vector<int>& nums) {
        n = nums.size();
        int sum = 0;
        for(int x: nums)
            sum += x;
        if(sum % 2) return false;
        else return findTargetSumWays(nums, sum / 2);
    }
    int findTargetSumWays(vector<int>& nums, int target)
    {
        vector<vector<bool>> dp(n + 1, vector<bool>(target + 1, false));
        for(int i = 0; i <= n; i++)
            dp[i][0] = true;
        for(int i = 1; i <= n; i++)
        {
            for(int cur = 0; cur <= target; cur++)
            {
                dp[i][cur] = dp[i - 1][cur];
                if(nums[i - 1] <= cur)
                    dp[i][cur] = dp[i][cur] || dp[i - 1][cur - nums[i - 1]];
            }
        }
        return dp[n][target];
    }
};

10.15 用栈操作构建数组 lc 1441

根据操作结果反向推出操作

class Solution {
public:
    vector<string> buildArray(vector<int>& target, int n) {
        int tn = target.size();
        vector<string> ans;
        int i = 1, j = 0;
        while(j < tn)
        {
            //
            if(i == target[j])
            {
                ans.push_back("Push");
                i++;
                j++;
            }
            while(i <= n && j < tn && i < target[j])
            {
                ans.push_back("Push");
                ans.push_back("Pop");
                i++;
            }
        }
        return ans;
    }
};

10.16 可能的二分法 lc 886

染色法判定二分图

const int N  = 20020;
const int M = 2010;


class Solution {
private:
    int h[N], e[N], ne[N], idx;
    int color[M];
public:
    void add(int a, int b)
    {
        e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
    }

    bool dfs(int i, int c)
    {
        color[i] = c;
        for(int j = h[i]; j != -1; j = ne[j])
        {
            int t = e[j];
            if(color[t] == c) return false;
            if(!color[t])
            {
                if(!dfs(t, 3 - c))
                    return false;
            }
        }
        return true;
    }
    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        memset(h, -1, sizeof h);
    
        for(int i = 0; i < dislikes.size(); i++)
        {
            int a = dislikes[i][0], b = dislikes[i][1];
            add(a, b);
            add(b, a);
        }
        for(int i = 1; i <= n; i++)
        {
            if(!color[i])
            {
                if(!dfs(i, 1))
                    return false;
            }
            cout << color[i] << endl;
        }
        return true;
    }
};

10.17 完全平方数

还是01背包问题，就是从平方和中选选到和为target的最小数量

class Solution {
public:
    const int INF = 0x3f3f3f3f;
    int numSquares(int n) {
        vector<int> sq;
        for(int i = 0; i * i <= n; i++)
            sq.push_back(i * i);
        int dp[n + 1];
        memset(dp, INF, sizeof dp);
        dp[1] = 1;
        dp[0] = 0; 
        for(int i = 0; i < sq.size(); i++)
        {
            for(int j = 0; j <= n; j++)
            {
                if(sq[i] <= j)
                    dp[j] = min(dp[j], dp[j - sq[i]] + 1);
            }
        }
        return dp[n];
    }
};

10.17 零钱兑换 lc 322

完全背包问题：物品可以无限使用，要求背包装满，要求使用的数量最少。

在满足：amount=v1x1+v2x2+v3x3+…+vnxn 的条件下，求： target=min{x1+x2+x3+…xn}可以dfs将所有的组合拿出来，然后取硬币数最小。

dp[i]表示硬币和为i时的最小硬币数，然后看取不取前i个硬币，取最小即可。

class Solution {
public:
    const int INF = 0x3f3f3f3f;
    int coinChange(vector<int>& coins, int amount) {
        int n = coins.size();
        int dp[amount + 1];
        memset(dp, INF, sizeof dp);
        dp[0] = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j <= amount; j++)
            {
                if(coins[i] <= j)
                {
                    dp[j] = min(dp[j], dp[j - coins[i]] + 1);
                }
            }
        }
        if(dp[amount] == INF)
            return -1;
        else
            return dp[amount];
    }
};

10.17 水果成篮 lc 904

滑动窗口应用 类似于lc992 //最多两个不同元素的最长连续子数组

理解题意：fruit[i] = 1表示种类1， 2表示种类2，0表示种类0，不是表示种类个数

class Solution {
public:
    int totalFruit(vector<int>& nums) {
        //最多两个不同元素的最长连续子数组
        unordered_map<int, int> hashmap;
        int ans = 0;
        int l = 0, r = 0;
        while(r < nums.size())
        {
            hashmap[nums[r++]]++;
            while(hashmap.size() > 2)
            {
                hashmap[nums[l]]--;
                if(!hashmap[nums[l]]) hashmap.erase(nums[l]);
                l++;
            }
            ans = max(ans, r - l);
        }
        return ans;
    }
};

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int n = fruits.size();
        int i = 0, j = 0, tot = 0, ans = 0;
        vector<int> cnt(n + 10, 0);
        for(int j = 0; j < n; j++)
        {
            if((++cnt[fruits[j]]) == 1)
                tot++;
            while(tot > 2)
            {
                if(--cnt[fruits[i++]] == 0)
                    tot--;
            }
            ans = max(ans, j - i + 1);
        }
        return ans;
    }
};

10.18 最大为 N 的数字组合 lc 902

数位dp

class Solution {
public:
    vector<int> d;
    int m;
    string sn;
    vector<int> dp;
    int atMostNGivenDigitSet(vector<string>& digits, int n) {
        for(int i = 0; i < digits.size(); i++)
            d.push_back(atoi(digits[i].c_str()));
        sn = to_string(n);
        m = sn.size();
        for(int i = 0; i < m; i++)
            dp.push_back(-1);
        return dfs(n, 0, true, false);
    }
    int dfs(int n, int i, bool isLimit, bool isNum)
    {
        if(i == m)
            return isNum;
        int ans = 0;
        if(!isLimit && isNum && dp[i] >= 0) return dp[i];
        if(!isNum)
            ans += dfs(n, i + 1, false, false);
        int up = isLimit? sn[i] - '0': 9;
        for(int j = 0; j < d.size(); j++)
        {
            if(d[j] > up)
                break;
            ans += dfs(n, i + 1, isLimit && d[j] == up, true);
        }
        if(!isLimit && isNum)
            dp[i] = ans;
        return ans;
    }
};

10.18 环形链表 lc 141

快慢指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == nullptr)
            return false;
        if(head->next == nullptr)
            return false;
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != nullptr)
        {
            slow = slow->next;
            fast = fast->next;
            if(fast != nullptr)
                fast = fast->next;
            if(slow == fast)
                return true;
        }
        return false;
    }
};

10.18 环形链表|| lc 142

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head, *slow = head;
        if(head == nullptr) return nullptr;
        if(head->next == nullptr) return nullptr;
        while(fast != nullptr)
        {
            slow = slow->next;
            fast = fast->next;
            if(fast != nullptr)
                fast = fast->next;
            if(fast == slow)
            {
                fast = head;
                while(fast != slow)
                {
                    fast = fast->next;
                    slow = slow->next;
                }
                return fast;
            }
        }
        return nullptr;
    }
};

10.18 删除链表的倒数第 N 个结点 lc 19

还是快慢指针找到倒数第n个节点然后再删除~下次再练习

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* p = head;
        if(head->next == nullptr)
            return nullptr;
        for(int i = 0; i < n; i++)
            p = p->next;
        ListNode* q = head;
        if(p == nullptr)
            return head->next;  //删掉头节点

        while(p->next != nullptr)
        {
            p = p->next;
            q = q->next;
        }
        ListNode* nx = q->next;
        q->next = nx->next; 
        return head;
    }
};

10.19 无法吃午餐肉的同学 lc 1700

模拟

class Solution {
public:
    int countStudents(vector<int>& students, vector<int>& sandwiches) {
        int n = students.size();
        int s0 = 0, s1 = 0;
        for(int x: students)
        {
            if(x)  s1++;
            else s0++;
        }
        for(int x: sandwiches)
        {
            if(x == 1 && s1 > 0) s1--;
            else if(x == 0 && s0 > 0) s0--;
            else break;
        }
        return s0 + s1;
    }
};

10.19 括号的生成 lc 22

回溯

class Solution {
public:
//主要是保证右括号不能在左括号之前生成
    vector<string> ans;
    string tmp;
    vector<string> generateParenthesis(int n) {
        dfs(n, n, tmp);
        return ans;
    }
    void dfs(int left, int right, string tmp)
    {
        if(left == 0 && right == 0)
        {
            ans.push_back(tmp);
            tmp = "";
            return;
        }
        if(left > 0)
            dfs(left - 1, right, tmp +'(');
        if(right > left)
            dfs(left, right - 1, tmp +')');
    }
};

10.19 组合总和 lc 39

回溯

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> tmp;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end());
        dfs(candidates, target, 0, 0);
        return ans;
    }
    void dfs(vector<int>& candidates, int target, int curSum, int i)
    {
        if(curSum == target)
        {
            ans.push_back(tmp);
            return;
        }
        if(curSum > target)
        {
            return;
        }
        for(int j = i; j < candidates.size(); j++)
        {
            tmp.push_back(candidates[j]);
            dfs(candidates, target, curSum + candidates[j], j);
            tmp.pop_back();
        }
    }
};

10.19 组合总数 II lc 40

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> tmp;
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end());
        dfs(candidates, target, 0, 0);
        return ans;
    }
    void dfs(vector<int>& candidates, int target, int cur, int last)
    {
        if(cur == target)
        {
            ans.push_back(tmp);
            return;
        }
        if(cur > target)
        {
            return;
        }
        for(int i = last; i < candidates.size(); i++)
        {
            if(i > last && candidates[i] == candidates[i - 1])
                continue;
            tmp.push_back(candidates[i]);
            dfs(candidates, target, cur + candidates[i], i + 1);
            tmp.pop_back();
        }

    }
};

10.19 电话号码的字母组合 lc 17

回溯

class Solution {
public:
    unordered_map<char, string> map;
    vector<string> ans;
    int n;
    string tmp;
    vector<string> letterCombinations(string digits) {
        n = digits.size();
        if(n == 0) return {};
        map['2'] = "abc";
		map['3'] = "def";
		map['4'] = "ghi";
		map['5'] = "jkl";
		map['6'] = "mno";
		map['7'] = "pqrs";
		map['8'] = "tuv";
		map['9'] = "wxyz";
        dfs(digits, 0, tmp);
        return ans;
    }
    void dfs(string digits, int i, string tmp)
    {
        if(tmp.size() == n)
        {
            ans.push_back(tmp);
            tmp = "";
            return;
        }
        int s = digits[i];
        for(int j = 0; j < map[s].size(); j++)
        {
            char ch = map[s][j];
            dfs(digits, i + 1, tmp + ch);
        }   
    }
};

10.20 缺失的第一个正数 lc 41

最大的缺失的正数也不会超过nums.size()。还是和下标相关

把每个数放在下标应该在的数上，然后从0开始判断如果和下标不一样的第一个数就是缺失的第一个正数。

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int n = nums.size();
        for(int i = 0; i < n; i++)
        {
            while(nums[i] > 0 && nums[i] < n && nums[i] != nums[nums[i] - 1])
                swap(nums[i], nums[nums[i] - 1]);
        }
        for(int i = 0; i < n; i++)
        {
            if(nums[i] != i + 1)
                return i + 1;
        }
        return n + 1;
    }
};

10.20 寻找重复数 lc 287

把数组看成链表，找到环的入口

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        //将数组看成链表,找到环的入口
        int slow = 0, fast = 0;
        while(1)
        {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if(slow == fast)
                break;
        }
        fast = 0;
        while(slow != fast)
        {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
};

10.20 找到所有数组中消失的数字 lc 448

就是把出现的数字和下标关联起来，将出现的数字的下标存储的数变成负数，最后是正数的就是缺失的。

class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> ans;
        for(int i = 0; i < nums.size(); i++)
        {
            nums[abs(nums[i]) - 1] = - abs(nums[abs(nums[i]) - 1]);
        }
        for(int i = 0; i < nums.size(); i++)
        {
            if(nums[i] > 0)
                ans.push_back(i + 1);
        }
        return ans;
    }
};

10.20 第K个语法符号lc 779

class Solution {
public:
    int kthGrammar(int n, int k) {
        if(n == 1)
            return 0;
        return !(k % 2)^kthGrammar(n - 1, (k + 1) / 2);
    }
};

10.21 股票价格跨度 lc 901

单调栈：单调递减栈，当出现新价格大于栈顶价格时，就需要pop找出栈里面所有小于的，保持单调递减

class StockSpanner {
public:
    stack<int> stk;
    vector<int> v;
    int idx = 0;
    StockSpanner() {
        idx++;
        v.push_back(INT_MAX);
        stk.push(0);
    }
    
    int next(int price) {
        v.push_back(price);
        while(stk.size() && v[stk.top()] <= price) {
            stk.pop();
        }
        int i = stk.top();
        stk.push(idx);
        return idx++ - i;
    }
};

10.22 根据身高重建队列 lc 406

按照身高从大到小排序，如果身高相同先排k小的。然后一个个插入，如果现有元素数量大于k的要求了，说明前面高个的太多了，需要把当前元素往前排。如果小于k的要求则直接插入即可，后面会随着插入而满足条件的。

struct peo
{
    int h, k;
};
bool cmp(const peo& p1, const peo& p2)
{
    if(p1.h != p2.h)
        return p1.h > p2.h;
    else return p1.k < p2.k;
}
class Solution {
public:
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        int n = people.size();
        peo P[n];
        for(int i = 0; i < n; i++)
        {
            P[i].h = people[i][0];
            P[i].k = people[i][1];
        }
        sort(P, P + n, cmp);
        vector<vector<int>> ans;
        for(int i = 0; i < n; i++)
        {
            if(ans.size() <= P[i].k)
                ans.push_back({P[i].h, P[i].k});
            else
                ans.insert(ans.begin() + P[i].k, {P[i].h, P[i].k});
        
        return ans;
    }
};

10.22 规划兼职工作lc 1235

按照endtime排序，然后dp[i]表示使用前i个元素的获得的最大报酬。

struct job {
    int s, e, p;
};
bool cmp(const job& j1, const job& j2) {
    return j1.e < j2.e;
}
class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int n = startTime.size();
        job jobs[n];
        for(int i = 0; i < n; i++) {
            jobs[i].s = startTime[i];
            jobs[i].e = endTime[i];
            jobs[i].p = profit[i];
        }
        sort(jobs, jobs + n, cmp);
        int dp[n];
        dp[0] = jobs[0].p;
        for(int i = 1; i < n; i++) {
            dp[i] = max(dp[i - 1], jobs[i].p);
            for(int j = i - 1; j >= 0; j--) {
                if(jobs[j].e <= jobs[i].s) {
                    dp[i] = max(dp[i], dp[j] + jobs[i].p);
                    break;
                }
            }
        }
        return dp[n - 1];
    }
};

10.24 除自身以外的乘积 lc 238

剑指offer中的一道题，前缀统计nums[i]左侧的，后缀统计nums[i]右侧的，一共O(n)

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans(n, 1);
        int pre = 1, suf = 1;
        for(int i = 0; i < n; i++) {
            ans[i] *= pre;
            pre *= nums[i];
        }
        for(int i = n - 1; i >= 0; i--) {
            ans[i] *= suf;
            suf *= nums[i];
        }
        return ans;
    }
};

10.24 和为k的子数组 lc 560

前缀和+哈希表

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> hmap;
        hmap[0] = 1;
        int sum = 0, ans = 0;
        for(int i = 0; i < nums.size(); i++) {
            sum += nums[i];
            if(hmap.count(sum - k)) {
                ans += hmap[sum - k];
            }
            hmap[sum]++;
        }
        return ans;
    }
};

10.24 分割数组 lc 915

只要左边的max <= 右边的min即可, O(n)的

右边的min可以先统计以下,最后加上一个INT_MAX哨兵

class Solution {
public:
    int partitionDisjoint(vector<int>& nums) {
        int mi = INT_MAX, ma = 0;
        vector<int> minNums(nums.size(), INT_MAX);
        for(int i = nums.size() - 1; i >= 0; i--) {
            mi = min(mi, nums[i]);
            minNums[i] = mi;
        }
        minNums.push_back(INT_MAX);
        for(int i = 0; i < nums.size(); i++) {
            ma = max(ma, nums[i]);
            if(ma <= minNums[i + 1]) {
                return i + 1;
            }
        }
        return 0;
    }
};

10.25 最短的桥 934

10.26 任务调度器 lc 621

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        int cnt[26];
        int max_cnt = 0, max_cnt_same = 0;
        memset(cnt, 0, sizeof cnt);
        for(int i = 0; i < tasks.size(); i++) {
            cnt[tasks[i] - 'A']++;
        }
        for(int i = 0; i < 26; i++) {
            max_cnt = max(max_cnt, cnt[i]);
        }
        for(int i = 0; i < 26; i++) {
            if(max_cnt == cnt[i]) {
                max_cnt_same++;
            }
        }
        int ans = (n + 1) * (max_cnt - 1) + max_cnt_same;
        //而当任务数超过该值时，我们可以在将其横向添加每个n+1 块的后面，同时不会引入额外的冻结时间
        return max(ans, tasks.size()); 
    }
};

10.26 和至少为k的最短子数组 lc 862

暴力解法（超时）：按照len遍历+滑动窗口，$O(n^2)$的复杂度（注意：所有sum小于k不一定代表里面没有大于等于k的子数组，因为有负数的存在）。

class Solution {
public:
    int shortestSubarray(vector<int>& nums, int k) {
        int n = nums.size();
        for(int len = 1; len <= n; len++) {
            int s = accumulate(nums.begin(), nums.begin() + len, 0);
            if(s >= k) return len;
            for(int l = 1; l  + len - 1 < n; l++) {
                int r = l  + len - 1;
                s = s + nums[r] - nums[l - 1];
                if(s >= k) return len;
            }
        }
        return -1;
    }
};

10.28 戳气球 lc 312

很难的区间dp

class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        nums.push_back(1);
        nums.insert(nums.begin(), 1);
        int dp[n + 2][n + 2];
        memset(dp, 0, sizeof dp);
        //全都戳破的上一个状态是只剩一个没被戳破
        //dp[l][r]不包含l, r中k表示最后戳破的气球,最后就剩下 l, k, r了
        for(int len = 3; len <= n + 2; len++) {
            for(int l = 0; l + len - 1 <= n + 1; l++) {
                int r = l + len - 1;
                for(int k = l + 1; k <= r - 1; k++) {
                    dp[l][r] = max(dp[l][r], dp[l][k] + dp[k][r] + nums[l] * nums[k] * nums[r]);
                }
            }
        }
        return dp[0][n + 1];
    }
};

10.28 子数组的最小值之和 lc 907

单调栈的应用题:计算每个值作为子数组最小值的次数,就需要分别向左向右找第一个小于arr[i]的值,假设最远子数组为(l, r),依据乘法原理子数组的个数就是(i - l) * (r - i)

还有很重要的一点就是:可能有重复的!

比如[1, 2, 3, 2, 3, 1]两个2计算的最远子数组都是(0, 5),那么就会在[1, 4]这个区间内重复计算两个2的子数组个数

我们需要向左找第一个小于的,向右找第一个小于等于的,那么这样左边的2最远子数组就是(0, 3),右边的就是(0, 5),这样就不会重复计算了!

class Solution {
public:
    const int mod = 1e9 + 7;
    int sumSubarrayMins(vector<int>& arr) {
        int n = arr.size();
        //加俩哨兵
        arr.push_back(0);
        arr.insert(arr.begin(), 0);
        int ans = 0;
        stack<int> stk;
        stack<int> stk1;
        int left[n + 2];
        int right[n + 2];
        stk.push(0);
        for(int i = 1; i <= n; i++) {
            while(!stk.empty() && arr[stk.top()] >= arr[i]) {
                stk.pop();
            }
            left[i] = i - stk.top();
            //cout << i << " " << left[i] << endl;
            stk.push(i);
        }
        stk1.push(n + 1);
        for(int i = n; i > 0; i--) {
            while(!stk1.empty() && arr[stk1.top()] > arr[i]) {
                stk1.pop();
            }
            right[i] = stk1.top() - i;
            stk1.push(i);
        }
        for(int i = 1; i <= n; i++) {
            ans =  (ans + (long long)left[i] * right[i] * arr[i]) % mod;
        }
        return ans;
    }
};

10.30 LRU缓存 lc 146

哈希表+ 双向链表：最关键的就是加上一个头节点和尾节点，剩下的就仔细写仔细调试就可以了。

struct Node
{
    int key;
    int value;
    Node* next;
    Node* pre;
    Node(int k, int v)
    {
        key = k;
        value = v;
        next = nullptr;
        pre = nullptr;
    }
};
class LRUCache {
public:
    Node* head;
    Node* nail;
    int cnt = 0;
    int cap;
    unordered_map<int, Node*> hashmap;
    LRUCache(int capacity) {
        cap = capacity;
        head = new Node(-1, -1);
        nail = new Node(-1, -1);
        head->next = nail;
        head->pre = nail;
        nail->next = head;
        nail->pre = head;
    }
    
    int get(int key) {
        if(hashmap.find(key) == hashmap.end())
            return -1;
        Node* tmp = hashmap[key];
        remove(tmp);
        addFromHead(tmp);
        return tmp->value;
    }
    void remove(Node* t)
    {
        hashmap.erase(t->key);
        Node* pt = t->pre;
        Node* nt = t->next;
        pt->next = nt;
        nt->pre = pt;
        cnt--;
    }
    void addFromHead(Node* t)
    {
        hashmap[t->key] = t;
        Node* nt = head->next;
        t->next = nt;
        t->pre = head;
        head->next = t;
        nt->pre = t;
        cnt++;
    }
    void put(int key, int value) {
        if(get(key) != -1)
        {
            head->next->value = value;
            return;
        }
        if(cnt < cap)
        {
            Node* tmp = new Node(key, value);
            addFromHead(tmp);
        }
        else
        {
            Node* tmp = new Node(key, value);
            Node* nt = nail->pre;
            remove(nt);
            addFromHead(tmp);
        }
    }
};

10.30 字母大小写全排列 lc 784

回溯

class Solution {
public:
    vector<string> ans;
    string tmp;
    vector<string> letterCasePermutation(string s) {
        dfs(s, 0);
        return ans;
    }
    void dfs(string s, int i)
    {
        if(i == s.size())
        {
            ans.push_back(tmp);
            return;
        }
        if(s[i] >= '0' && s[i] <= '9')
        {
            tmp += s[i];
            dfs(s, i + 1);
            tmp.pop_back();
        }
        else if(s[i] >= 'a' && s[i] <= 'z')
        {
            tmp += s[i];
            dfs(s, i + 1);
            tmp.pop_back();
            tmp += (s[i] - 32);
            dfs(s, i + 1);
            tmp.pop_back();
        }
        else
        {
            tmp += s[i];
            dfs(s, i + 1);
            tmp.pop_back();
            tmp += (s[i] + 32);
            dfs(s, i + 1);
            tmp.pop_back();
        }
    }
};

10.30 最小栈 lc 155

两个栈辅助的

class MinStack {
public:
    stack<int> stk;
    stack<int> minstack;
    MinStack() {

    }
    
    void push(int val) {
        stk.push(val);
        if(minstack.empty() || val <= minstack.top())
            minstack.push(val);
    }
    
    void pop() {
        int x = stk.top();
        cout << x << endl;
        stk.pop();
        if(minstack.size() && x == minstack.top())
            minstack.pop();
    }
    
    int top() {
        return stk.top();
    }
    
    int getMin() {
        cout << minstack.top() << endl;
        return minstack.top();
    }
};

链表解决的：头插法，每个节点中记录栈顶当前值和当前值作为栈顶时的最小值。

struct node
{
    int val;
    int min;
    node* next;
    node(int x, int y)
    {
        val = x;
        min = y;
        next = nullptr;
    }
};
class MinStack {
public:
    node* head;
    MinStack() {
        head = nullptr;
    }
    
    void push(int val) {
        if(head == nullptr)
            head = new node(val, val);
        else
        {
            int m = val <= head->min? val: head->min;
            node* tmp = new node(val, m);
            tmp->next = head;
            head = tmp; 
        }
    }
    
    void pop() {
        head = head->next;
    }
    
    int top() {
        return head->val;
    }
    
    int getMin() {
        return head->min;
    }
};

10.31 滑动窗口的最大值 lc 239

模拟滑动窗口不行因为如果排出最大值要重新遍历找最大值,会超时

因此,选择双向队列维护一个单调递减的队列,当删掉的值==左边最大值时,将其删掉.当加入的值大于队尾的值时,删掉队尾维持递减队列.

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> ans;
        int n = nums.size();
        deque<int> q;
        int l = 0, r = k - 1;
        for(int i = l; i <= r; i++)
        {
            while(q.size() && nums[i] > q.back())
                q.pop_back();
            if(!q.size() || nums[i] <= q.back())
                q.push_back(nums[i]);
        }
        ans.push_back(q.front());
        while(r + 1 < n)
        {
            if(q.size() && nums[l] == q.front())
                q.pop_front();

            while(q.size() && nums[r + 1] > q.back())
                q.pop_back();
            q.push_back(nums[r + 1]);
            ans.push_back(q.front());
            l++;
            r++;
        }
        return ans;
    }
};

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int> q;
        vector<int> ans;
        for(int i = 0; i < nums.size(); i++) {
            if(!q.empty() && i >= k && nums[i - k] == q.front()) {
                q.pop_front();
            }
            while(!q.empty() && nums[i] > q.back()) {
                q.pop_back();
            }
            q.push_back(nums[i]);
            if(i >= k - 1) {
                ans.push_back(q.front());
            }
        }
        return ans;
    }
};

10.31 神奇字符串 lc481

模拟题目即可,小技巧 1^3 = 2 2^3 = 1

class Solution {
public:
    int magicalString(int n) {
        int x1 = 3, x2 = 3;  //x1是总的字符串数量,x2是生成到哪一个
        vector<int> s(4, 0);
        s[1] = 1; s[2] = 2; s[3] = 2;
        int cnt = 1, f = 1;;
        while(x1 < n)
        {
            int t = 0;
            if(s[x2] == 1)
            {
                s.push_back(f);
                cnt += (f == 1);
                x1++;
            }
            else
            {
                s.push_back(f);
                s.push_back(f);
                x1 += 2;
                cnt += (f == 1) * 2;
            }
            f = f ^ 3;
            x2++;
        } 
        if(x1 > n && s[x1] == 1) cnt--;
        return cnt;
    }
};

10.31 课程表 lc 207

气死我了,一个拓扑排序写了这么久…

const int N = 5010;
int h[N], e[N], ne[N], idx;
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        idx = 0;
        int inorder[numCourses];
        queue<int> q;
        memset(h, -1, sizeof h);
        memset(inorder, 0, sizeof inorder);
        for(int i = 0; i < prerequisites.size(); i++) {
            add(prerequisites[i][1], prerequisites[i][0]);
            inorder[prerequisites[i][0]]++;
        }
        for(int i = 0; i < numCourses; i++) {
            if(inorder[i] == 0) {
                q.push(i);
                inorder[i] = -1;
            }
        }
        int cnt = 0;
        while(!q.empty()) {
            int t = q.front();
            q.pop();
            cnt++;
            for(int i = h[t]; i != -1; i = ne[i]) {
                int b = e[i];
                inorder[b]--;
                if(!inorder[b]) {
                    q.push(b);
                }
            }
        }
        return cnt == numCourses;
    }
};

ans.push_back(q.front());
while(r + 1 < n)
{
if(q.size() && nums[l] == q.front())
q.pop_front();

        while(q.size() && nums[r + 1] > q.back())
            q.pop_back();
        q.push_back(nums[r + 1]);
        ans.push_back(q.front());
        l++;
        r++;
    }
    return ans;
}

};

```C++
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int> q;
        vector<int> ans;
        for(int i = 0; i < nums.size(); i++) {
            if(!q.empty() && i >= k && nums[i - k] == q.front()) {
                q.pop_front();
            }
            while(!q.empty() && nums[i] > q.back()) {
                q.pop_back();
            }
            q.push_back(nums[i]);
            if(i >= k - 1) {
                ans.push_back(q.front());
            }
        }
        return ans;
    }
};

10.31 神奇字符串 lc481

模拟题目即可,小技巧 1^3 = 2 2^3 = 1

class Solution {
public:
    int magicalString(int n) {
        int x1 = 3, x2 = 3;  //x1是总的字符串数量,x2是生成到哪一个
        vector<int> s(4, 0);
        s[1] = 1; s[2] = 2; s[3] = 2;
        int cnt = 1, f = 1;;
        while(x1 < n)
        {
            int t = 0;
            if(s[x2] == 1)
            {
                s.push_back(f);
                cnt += (f == 1);
                x1++;
            }
            else
            {
                s.push_back(f);
                s.push_back(f);
                x1 += 2;
                cnt += (f == 1) * 2;
            }
            f = f ^ 3;
            x2++;
        } 
        if(x1 > n && s[x1] == 1) cnt--;
        return cnt;
    }
};

10.31 课程表 lc 207

气死我了,一个拓扑排序写了这么久…

const int N = 5010;
int h[N], e[N], ne[N], idx;
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        idx = 0;
        int inorder[numCourses];
        queue<int> q;
        memset(h, -1, sizeof h);
        memset(inorder, 0, sizeof inorder);
        for(int i = 0; i < prerequisites.size(); i++) {
            add(prerequisites[i][1], prerequisites[i][0]);
            inorder[prerequisites[i][0]]++;
        }
        for(int i = 0; i < numCourses; i++) {
            if(inorder[i] == 0) {
                q.push(i);
                inorder[i] = -1;
            }
        }
        int cnt = 0;
        while(!q.empty()) {
            int t = q.front();
            q.pop();
            cnt++;
            for(int i = h[t]; i != -1; i = ne[i]) {
                int b = e[i];
                inorder[b]--;
                if(!inorder[b]) {
                    q.push(b);
                }
            }
        }
        return cnt == numCourses;
    }
};