实验室地震学中的电声发射与断裂复杂性

8 复杂性在实验室地震学中的研究：从电学和声学发射到断裂

瓦西里斯·萨尔塔斯1, 菲利波斯·瓦利亚纳托斯1, 迪莫斯·特里安蒂斯2, 伊利阿斯·斯塔夫拉卡斯2
1 克里特技术教育学院与联合国教科文组织固体地球物理学与地质灾害风险减缓教席，希腊克里特岛哈尼亚
2 西阿提卡大学，雅典，希腊

8.1 引言

众所周知，在岩石等脆性材料上施加机械应力时，会伴随电磁和声发射（AE）、红外辐射以及其他断裂发射现象（电子、原子、分子等的发射）。所有这些断裂诱发现象在诸多应用中具有重要意义，例如用于材料和地下矿山健康监测以及地震预测的前兆信号的搜寻。因此，关于这些不同的潜在物理过程，已通过实验和理论角度进行了广泛研究。

本文重点研究瞬态微弱电流和弹性波的发射，它们分别是压力激发电流（PSCs）技术和著名的声发射监测技术的基础（斯塔夫拉卡斯等人，2003，2004）。准脆性非金属材料中的微裂纹发展会因电偶极子的形成而产生电荷，这些电偶极子通常构成一个复杂的带电系统（瓦罗佐斯等人，2002；瓦利安托斯等人，2004）。此类电偶极子在裂纹两侧产生电势，从而导致电流流动。PSCs通过高灵敏度静电计和一对电极进行检测，该对电极安装在承受力学应力试验的试样表面适当位置上。

检测此类电流可能作为大规模断裂的前兆而具有重要意义，且已在实验室（瓦利安托斯等人，2004；特里安蒂斯等人，2007；弗里德等人，2009）和地球动力学尺度（诺米科斯和瓦利安托斯，1997；诺米科斯等人，1997；瓦罗佐斯，2005）上进行了测量。具体而言，在对岩石施加机械加载直至破坏的过程中，对其破坏前后微弱电流的发射现象已在近几十年中得到广泛研究，并针对干燥和湿润的岩石样本（如大理岩和角闪岩）开展了大量实验，发表了众多研究成果（斯塔夫拉卡斯等，2004；特里安蒂斯等人，2006，2008，2012）。这些研究中的科学挑战在于如何将实验室发现应用于理解大地尺度现象，例如关于地震电前兆的野外观测（瓦罗佐斯，2005）。

断裂诱发现象表现出长程相互作用、分形性和记忆效应，从这个意义上讲，它们可以用尺度不变定律来描述。定性而言，地震机制与材料内部裂纹的形成/扩展之间的相似性非常明显（瓦利安托斯和萨姆蒙兹，2010，2011；瓦利安托斯等人，2012a,b，2013a）。最近通过在单轴压缩孔隙率为40%的介孔二氧化硅陶瓷过程中进行声发射监测，研究了断裂实验与统计地震学基本定律（古登堡—里希特定律、大森定律、余震产出率和等待时间标度定律）之间的相似性（Baró 等人，2013）。

近年来，据报道，全球、区域和局部尺度上地震群体的集体特性可以通过非广延统计物理（NESP）得到很好的描述。同类型的统计物理也被证明适用于描述在实验室尺度下观察到的类似现象，例如在对岩石施加机械应力过程中产生的微裂纹以及释放的压力诱导微弱电流（瓦利安托斯等人，2012a,b,c，2013a,b；瓦利安托斯和特里安蒂斯，2012）。在此背景下，后续章节将研究压力诱导的声波和微弱电流的发射。

8.2 声发射与压力激发电流实验研究：实验室与现场观测

8.2.1 实验技术基础

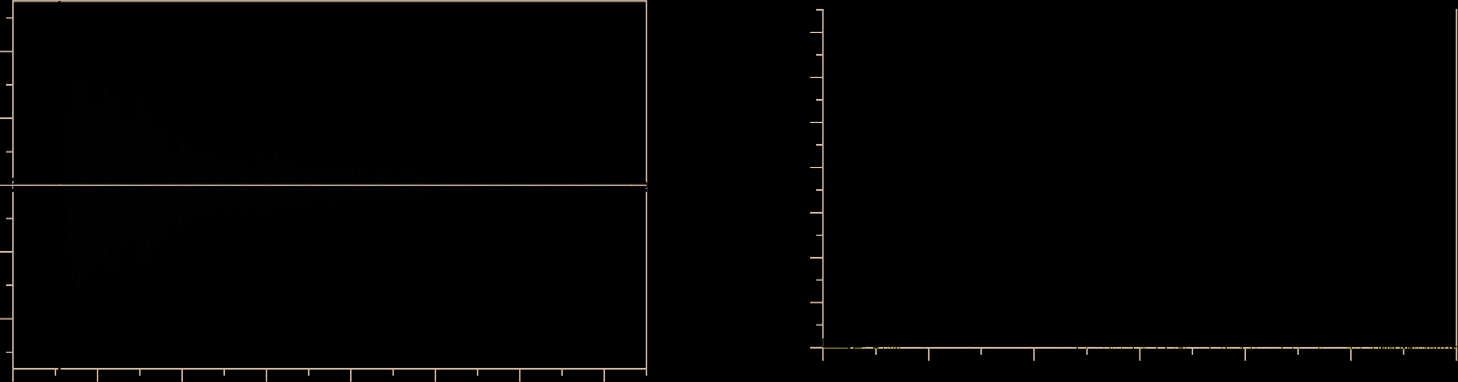
通过成熟的无损技术——声发射，可以研究岩石样品内部压力诱发的微裂纹的产生和传播。在声发射技术中，将压电传感器适当地附着在岩石试样表面，以记录由于裂纹形成与扩展而产生的弹性波。记录到的信号可通过多种声发射参数进行分析，例如事件率或累计击中次数（或事件）、幅度（分贝）和绝对能量、上升时间以及上升角等（见图 8-1）。声发射事件数量反映了扩展中的微裂纹的数量，而其幅度则与裂纹扩展增量长度相关。在受力岩石试样损伤累积过程中，还可将声发射信号与发射的压力激发电流结合进行分析和研究。这两种技术的相关性将使我们更深入地了解观测到的前兆信号的相关物理机制的起源。这种相关性将在下一节中详细阐述。

声发射和压力激发电流实验是在高容量加载框架（≥ 300 kN）下进行的，采用准静态加载或位移控制模式，具体取决于所进行的实验。每次实验前均进行初步试验，以评估特定批次试样的强度。

关于压电性电流技术，测量系统由超灵敏可编程静电计（吉时利6517A）和多通道电流卡（吉时利6521扫描卡）组成，记录电流范围从0.1飞安至20毫安，分为多个量程。静电计的数据通过GPIB接口存储在计算机中。

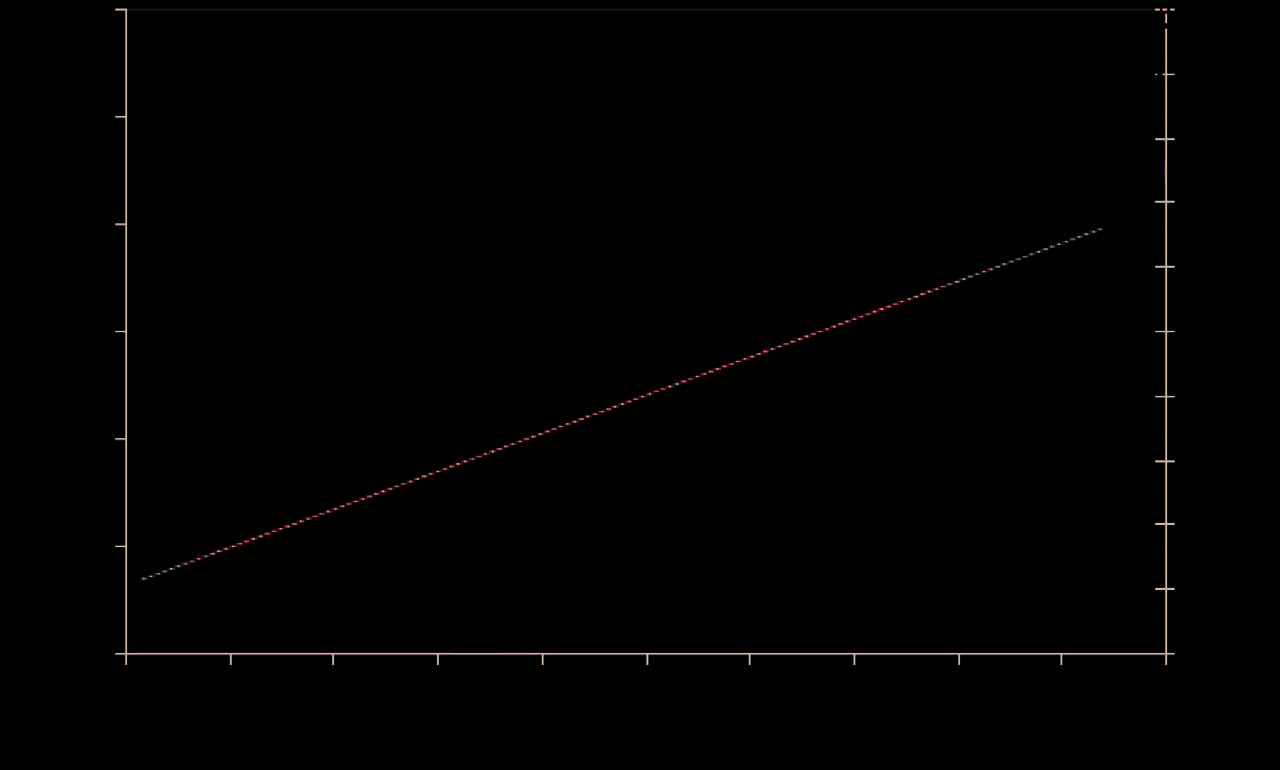
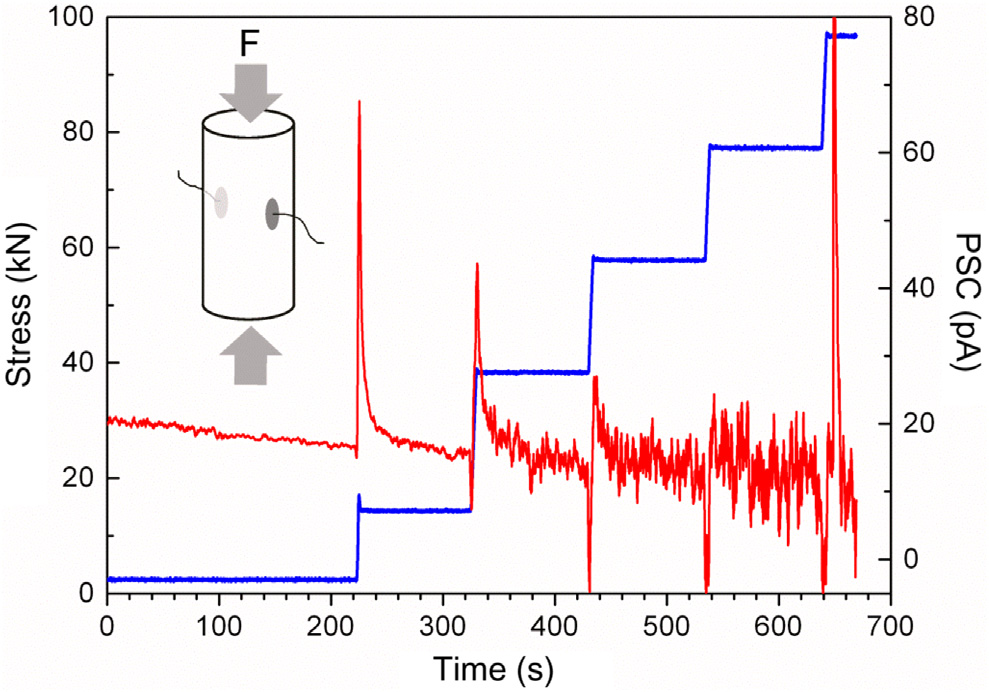
传感系统由沿加载轴安装的电极对组成，能够尽可能接近电流潜在源（或等效地，损伤发生的任何位置）采集电信号发射。电极网格在试样表面的分布取决于加载协议、试样的尺寸和形状。图8-2展示了在单轴加载大理岩试样过程中，压力激发电流信号随归一化应力和轴向应变变化的一个典型记录。在图8-3中，显示了大理岩试样在阶梯式加载实验中直至最终破坏的压力激发电流记录，各加载步之间有足够的时间使压力激发电流松弛（见图8-3）。关于压力刺激电流的定性和定量描述将在后续章节中给出。

为了检测声发射活动，使用了双通道声发射卡（物理声学公司的PCI‐2）。声发射传感器采用R15a（150kHz谐振频率）或宽带皮秒传感器，并将其放置在适当位置，以实现对声发射事件的三维定位，并估算声发射源的特征（幅度、能量和破裂模式）。声发射传感器通过真空润滑脂或硅胶固定在试样上。前置放大器增益为40分贝增益，声发射幅度的阈值通常设置为40分贝。

除了电极和声发射传感器外，还在试样的中点高度处粘贴了电阻应变片，以测量压缩加载过程中的轴向和/或横向应变。实验采用了协和应变片与Microlink 770电阻电桥配合使用。施加的力和产生的应变均通过吉时利制造的KUSB‐3100模数数据采集模块进行数字化并传输至计算机。

8.2.2 应力诱发岩石断裂过程中压力刺激电流与声发射的特征

已提出多种电化机制来解释在承受机械应力的岩石试样接近破坏时观测到的弱瞬态电流发射现象，该现象与材料中微裂纹的开启和扩展有关（弗罗因德，2002；拉夫罗夫，2005；布莱尔等，2010）。这些由微破裂引发的电化机制包括：（1）由于渗透性岩石中水流产生的电动效应，其中重力和地壳应变是驱动力；（2）含石英岩石中的压电效应；（3）无石英岩石中正电荷空穴的激活；（4）带电位错运动（MCDs）；（5）流动气体；以及（6）由声波驱动的导电地壳材料的运动。

所有这些机制都应与地震事件发生前或同时观测到的电记录一致，并且它们可能共同导致自发电荷产生的整体表现。然而，每种可能机制的效率及其（建设性或破坏性）相互作用仍有待研究。

MCD电化机制最初由斯利夫金（1993）提出，并由瓦里安托斯和察尼思（1998, 1999, 2003）以及察尼思和瓦里安托斯（2002）进一步发展，该机制因其与压电性岩石和非压电性岩石中的脆性断裂相关而具有很强的吸引力。根据该模型，电流密度被定义为极化变化率，其表达式如下：

$$
J = \frac{\partial P}{\partial t} = \sqrt{2} \cdot \frac{\Lambda_1 - \Lambda_2}{\Lambda_1 + \Lambda_2} \cdot \frac{ql}{b} \cdot \frac{d\varepsilon}{dt}
\quad (8.1)
$$

其中，$\Lambda_1$ 是为适应单轴压缩所需的刃型位错密度，$\Lambda_2$ 是相反类型的相应位错密度，$ql$ 是位错上的单位长度电荷，$b$ 为伯格向量，$d\varepsilon/dt$ 为应变率。公式(8.1) 表明，记录到的瞬态电流与非稳态变形的累积有关。在样品发生弹性变形的情况下，$\sigma = Y_o \cdot \varepsilon$，其中 $Y_o$ 为材料的杨氏模量，且应力率与应变率成正比。因此，根据公式(8.1)，压力激发电流（PSC）应与应变率成正比，即 $J \sim \partial\sigma/\partial t$。这意味着当岩石试样以恒定速率受力时，在弹性区域不应观察到任何瞬态 PSC 效应。然而，当应力进入微裂纹形成并扩展的塑性变形区时，杨氏模量不再保持恒定，而应考虑有效杨氏模量 $Y_{eff}$（$\sigma = Y_{eff} \cdot \varepsilon$）。在这种情况下，应变率增加，从而导致 PSC 也随之增加。

MCD模型的前述考虑已通过实验验证，这些实验是在干燥大理石试样上进行的，试样承受不同应力模式（恒定应力率、阶梯状应力和循环载荷）的单轴加载（Stavrakas 等，2004；瓦利安托斯等人，2004）。如图 8-4 所示，发射的压力激发电流（曲线b）在狄俄尼索斯大理石试样进行阶梯式单轴加载且应力处于弹性区域时，随应力率（曲线c）变化。

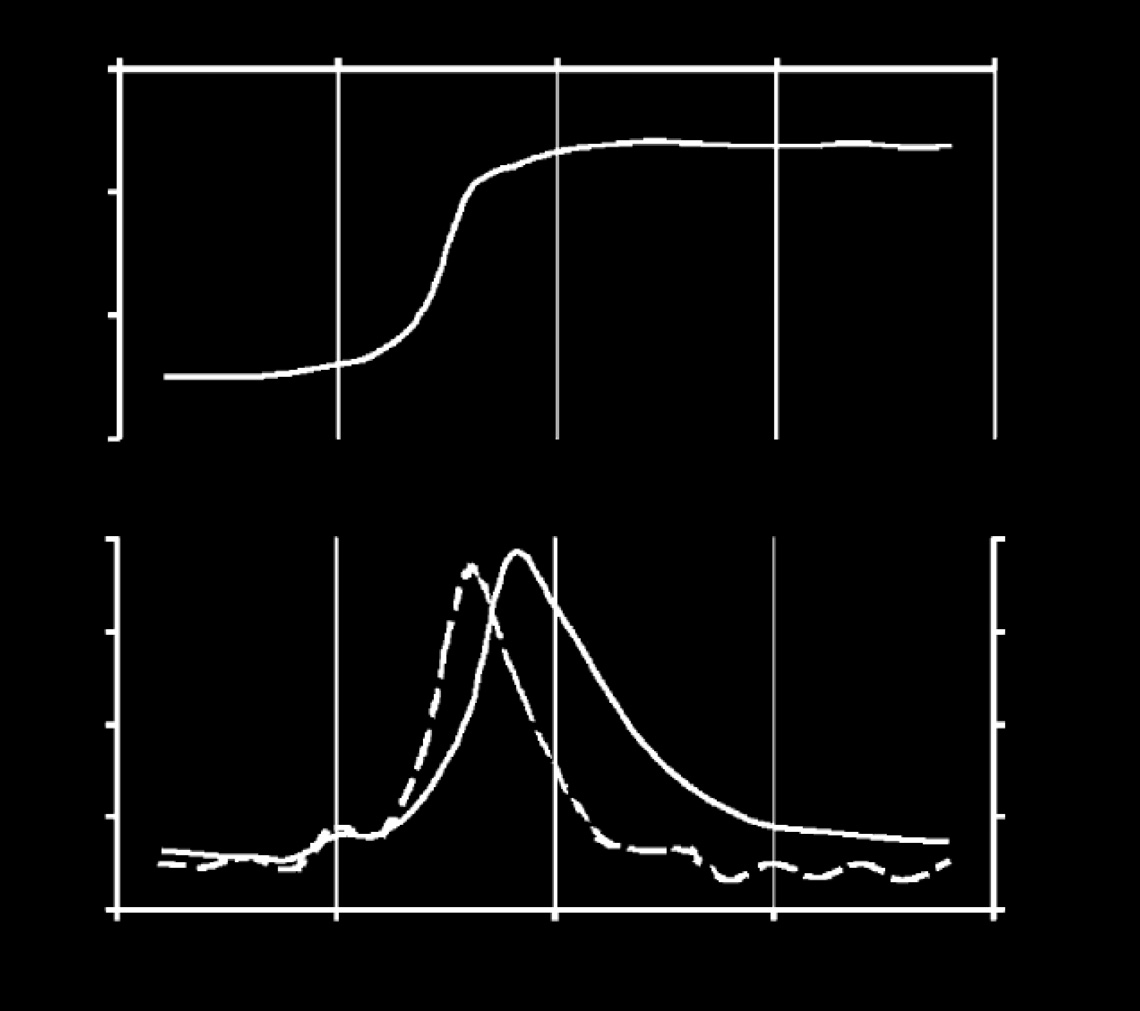
在狄俄尼索斯大理石试样进行阶梯式单轴加载且应力处于弹性区域时，记录到的压力刺激电流最大值与相应的峰值应力速率成正比。对于承受恒定应力率直至破坏的大理岩试样，仅当应力进入塑性变形范围时才观测到压力刺激电流（Triantis 等，2006；Pasiou 和 Triantis，2017）。

在恒定应变率（5×10⁻⁴ mm/s）下单轴压缩应力作用下，从大理石试样记录到的压力激发电流信号的典型变化如图 8-5所示。观察该图可区分出四个明显不同的区域。首先，在低应力值时观察到轻微的压力激发电流激发（t < 500 s），这可能与孔隙闭合过程有关。当材料进入线性应力‐变形区域时，杨氏模量持续增加并保持恒定。随后，压力激发电流达到非常低的值且波动较小（500 < t < 1500 s）。在此阶段，材料的力学行为仍处于弹性区域，同时杨氏模量保持恒定。接着，当材料进入塑性变形区时，压力激发电流显著增加（1500 < t < 2200 s）。压力激发电流在接近最大应力值时达到峰值。最后，当达到最大应力值后，压力激发电流出现反向极性，并表现出剧烈波动。在此范围内，宏观裂纹相继连续发展。

关于实验测试中加载直至破坏时释放的总电荷 $Q_t = \int I_{PSC}(t) dt$，PSCs的另一特性似乎与施加的应力率无关。在大理岩试样上进行的实验证实了这一事实，同时也得到了理论上的验证（Triantis 等，2006）。已对大理岩样品中电荷释放的时间演化进行了研究，发现电荷与变形之间存在线性关系。当施加的应力高于屈服应力值时，这种线性关系开始成立，并一直保持到试样接近破坏为止（特里安蒂斯等人，2008）。该线性关系的实验验证与MCD模型的理论预测一致。需要注意的是，根据MCD模型，电流密度与应变率之间存在类比关系。

先前在实验室尺度下对压力激发电流的实验观测结果可通过MCD模型进行解释，原则上可应用于产生电前兆信号的大地尺度地震事件。如果是这样，那么记录到的许多地震事件的电前兆信号可归因于微裂纹形成与扩展的集体作用，这种作用在更大尺度上累积损伤（瓦利安托斯和察尼斯，1998，1999，2003；察尼斯和瓦利安托斯，2002）。

值得一提的是，当岩石试样在先前的应力循环中已经遭受损伤时，后续加载循环产生的压力激发电流幅度将小于前一次载荷产生的幅度（见瓦利安托斯等人，2004中的图5）。这构成了另一种特征性质，类似于已研究过的声发射现象，称为凯撒效应（记忆效应）。

最近的一项出版物（斯塔夫拉卡斯，2017）描述了在顺序加载循环期间压力激发电流信号与声发射释放之间的相关性。根据凯撒效应，在施加的机械应力低于试样先前所受的任何应力时，检测到无声发射活动。这一观察结果清楚地表明，当施加的机械应力不高于先前施加的任何应力时，试样整体中的不连续性不会进一步扩展。与凯撒效应相反，对试样力学质量的定量估计被称为费利西蒂效应。表现出费利西蒂效应的试样即使在低于先前施加应力值的应力下也会产生声发射活动（见图 8-6）。这可以通过费利西蒂比（FR）进行定性评估，该比值定义为声发射释放开始时的施加载荷与先前施加的最大载荷最大值之比。因此，凯撒效应对应的FR等于1。FR越低，表明被测试试样的力学状态可能越临界。关于压力激发电流信号，可以引入类似的比值：$R_{PSC}$。具体而言，$R_{PSC}$ 可定义为压力激发电流开始超出背景值（$PSC_b$）时的应力值与先前施加的最大应力值之比。图 8-7展示了对一个狄俄尼索斯大理石试样进行压缩试验期间记录的压力刺激电流，该试验包括三个连续的加载-卸载循环。我们明显观察到，在每一次重复循环中压力激发电流显著减小，而当施加载荷超过60兆帕且试样接近破坏时，检测到强烈的PSC辐射。在此特定实验中，第二次加载时的$R_{PSC}$比值为0.78，而在第三次加载时达到0.94。

值得注意的是，一些研究人员已采用压力激发电流技术，而其他研究人员则使用了类似的技术（Cartwright-Taylor et al., 2014；Li et al., 2015；）

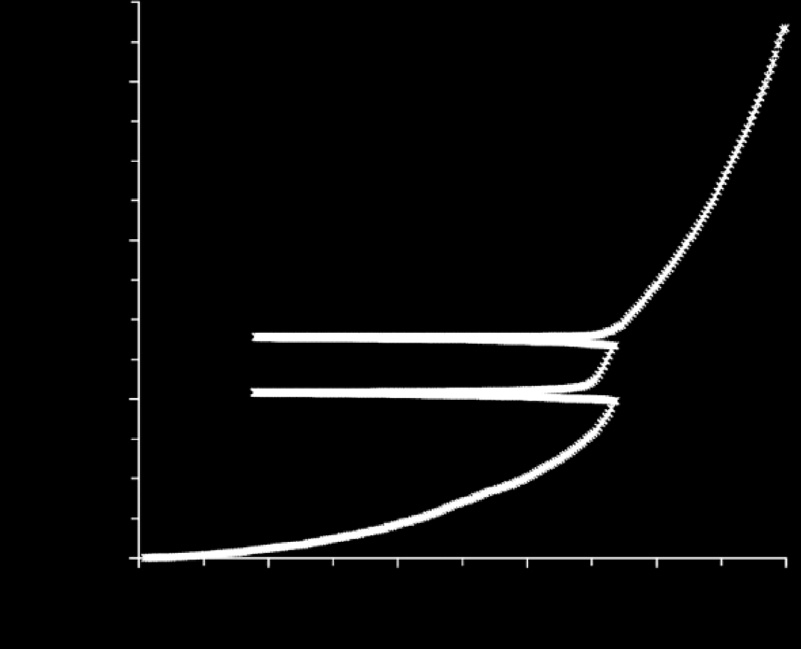
阿彻等，2016；弗萨等人，2016，2017）。例如，压力激发电流技术已应用于从北京长沟峪煤矿冲击地压煤矿样品中提取的煤岩（李等人，2015）。根据煤样研究结果，当施加载荷处于弹性变形阶段时，电流变化较弱。当煤样出现塑性变形时，随着载荷增加，电流迅速上升。一旦达到峰值应力，试样进入不稳定破坏阶段，电流出现显著反向。这一观测构成了压力激发电流信号的特征性特征，并已被多次证实和报道。

8.2.3 声发射与PSC特征的定性相关性

压力激发电流与声发射的相关性是一个引起广泛关注的研究领域（参见例如 斯塔夫拉卡斯等人，2015 及其中参考文献）。具体而言，旨在研究声发射与压力激发电流记录之间的相似性，因为声发射是一种直接方法，可提供试样在承受机械加载时其力学状态的信息。需要注意的是，声发射测量早已被采用为一种无损检测方法，用于研究发生在试样内部的微破裂过程的力学特性（即应力矢量方向、弹性波速度、剪切-拉伸或混合模式断裂）。

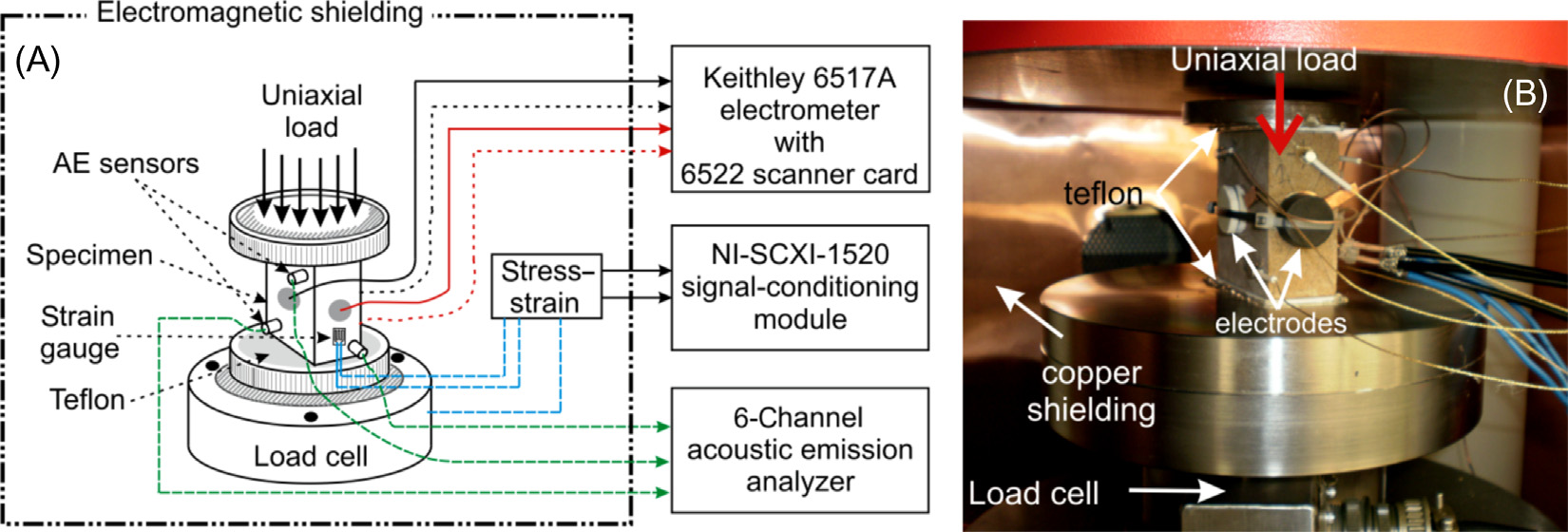
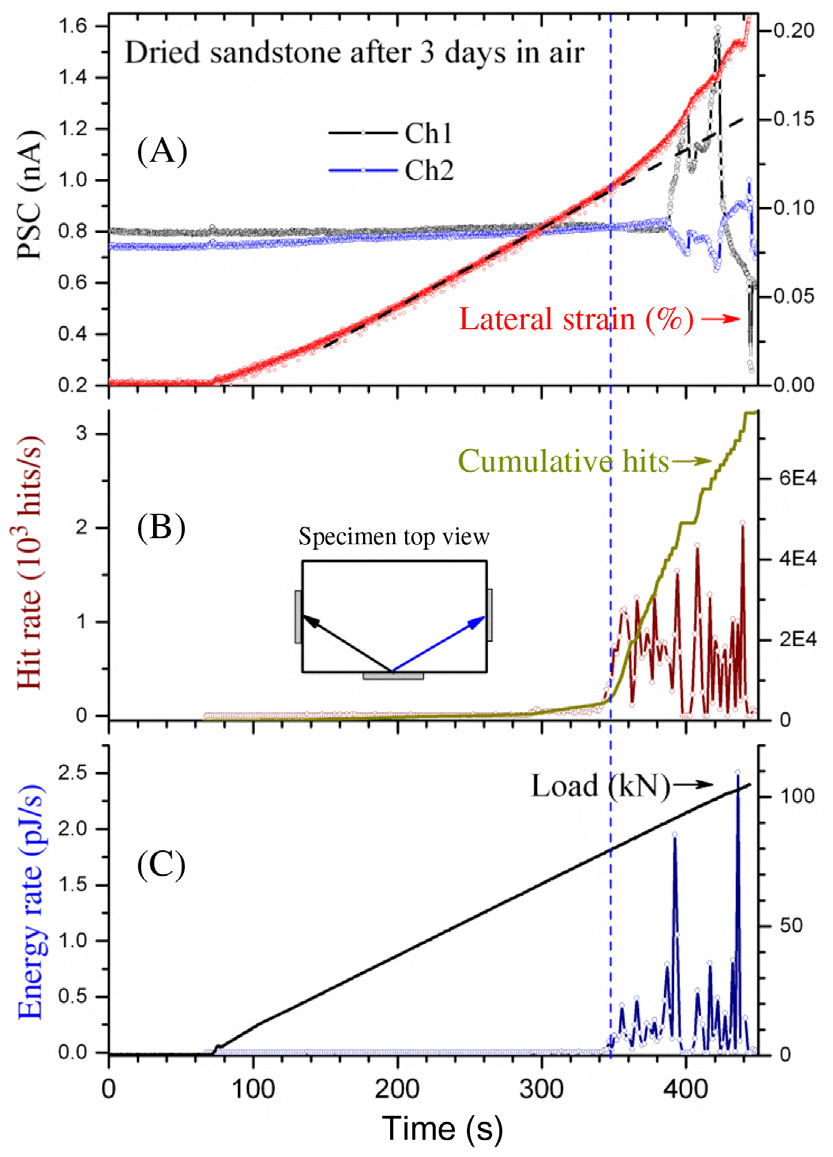
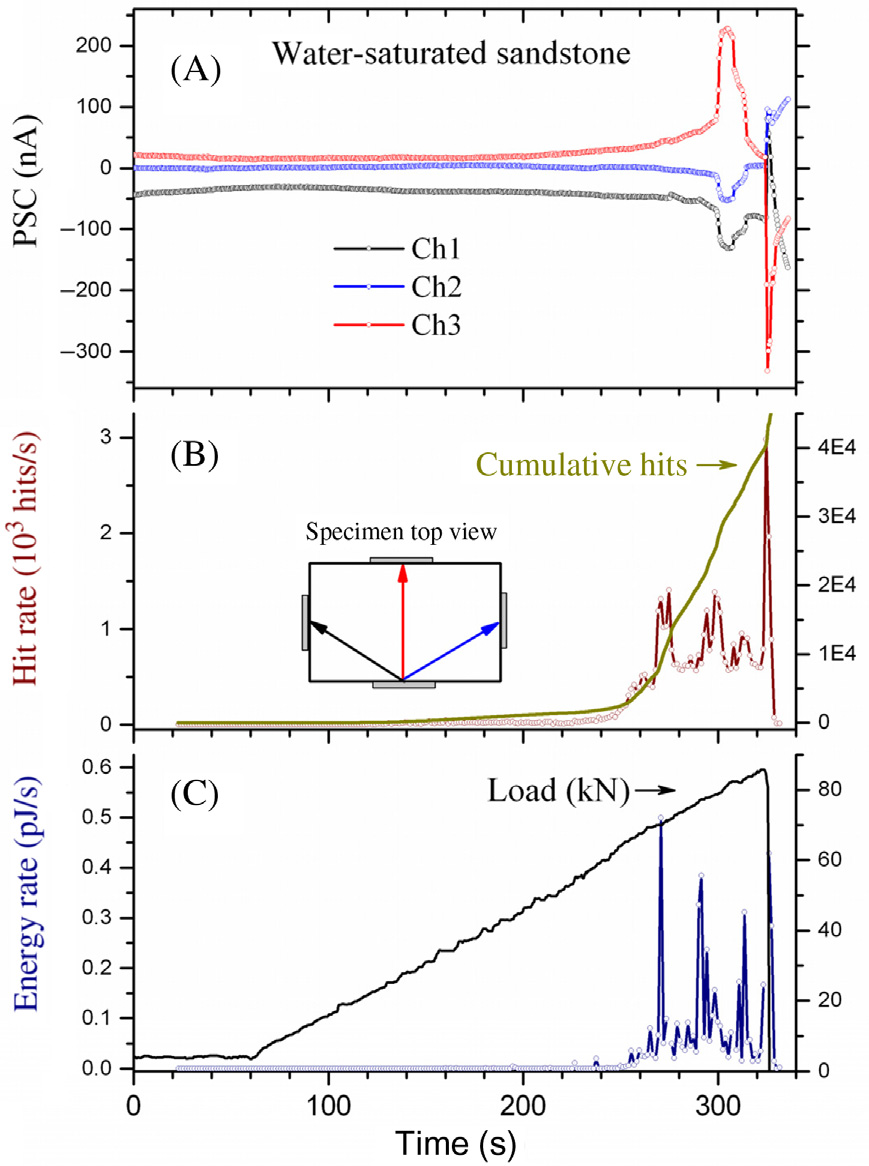
已对多孔砂岩样品在单轴加载条件下进行声发射活动与PSC辐射的同步测量，以研究含水量和孔隙流体的作用（Saltas et al., 2015）。PSCs在垂直于施加应力的不同方向上被记录，同时使用一组声发射皮传感器同步记录声发射事件。实验装置如图 8-8所示。在干燥砂岩试样的单轴加载过程中，弱电流（小于2 nA）在破坏的最终阶段（385 s后）被检测到，如图 8-9A所示。然而，显著的声发射活动则更早开始（在340 s左右），大约在破裂载荷的75% 时，由图 8-9B和C中增加的撞击次数（或能量）速率可以看出。这大致对应于通过微裂纹生成从弹性范围向脆性变形的转变。相对于先前的声发射活动，PSC发射的延迟现象可归因于存在临界浓度的微裂纹，这些微裂纹使得重新分布的电荷能够在砂岩试样内部实现电荷输运。每个通道记录到不同极性的PSC强度不同，表明由于裂纹形成与扩展产生的微弱电流在整体内不均匀地发射，具有与破坏前试样内部形成定向剪切面相关的优势方向。

对于水饱和砂岩（图 8-10），压力刺激电流的强度比低含水量的试样（即在空气中放置3天的干燥试样）观测到的强度高出近三个数量级（图 8-9）。在后一种情况下，缺乏自由水或弱结合水应会抑制微弱电流。然而，在水饱和砂岩中，孔隙体积中的自由水存在会显著影响导电路径，导致发射电流值更高。最后，在盐水饱和砂岩的情况下，由于离子电荷过剩，发射电流比在水饱和砂岩中记录的值甚至高出约一个数量级。无论样品的含水量如何，声发射活动在所有情况下均表现出相似的特征。

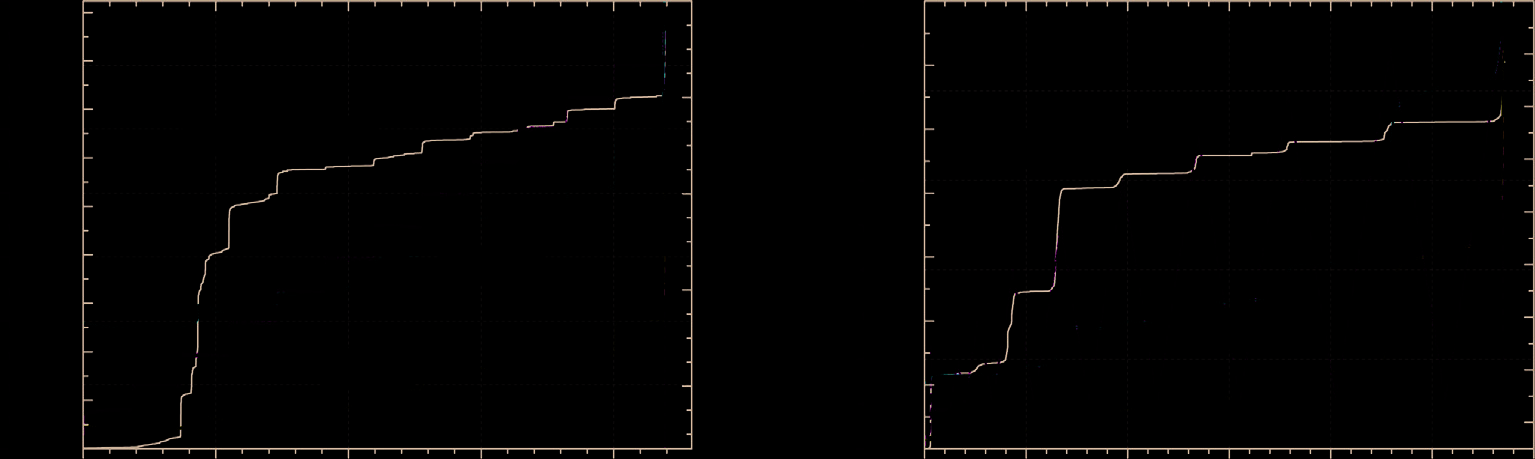
为了研究岩石在机械应力作用下电学性质随压力的变化，萨尔塔斯等人（2014）对经历线性和阶梯式单轴加载的石灰岩样品进行了复电导阻抗与声发射联合测量。值得注意的是，他们发现晶粒内部和晶界的直流电导率均随着单轴加载的增加而增加，表明在较高的单轴应力下活化体积为负值，范围从-10 到 -61 cm³/mol。这一发现，结合其他研究中报道的含水岩石（如白榴岩、花岗闪长岩和角闪岩）中出现的负活化体积（尚克兰德等人，1997；帕帕萨西亚斯等人，2010、2011、2012），对于正确记录地震事件发生前和/或期间产生的地震电信号的物理机制至关重要（瓦罗佐斯和亚历克索普洛斯，1984、1987；瓦罗佐斯，2005）。此外，他们还报告称，石灰岩在线性加载过程中的交流电导率与声发射活动密切相关，遵循材料断裂前能量释放的临界现象普遍自相似规律。在其他类型的单轴加载（如阶梯式和锯齿状加载）中，也观察到了声发射活动与交流电导率之间的这种强相关性，如图 8-11所示。

在每种情况下，记录通道的累计击中次数表现出与交流电导率相同的特征。然而，在较长时间的阶梯式加载实验中（图 8-11A），当载荷保持恒定时，电导率的逐渐下降明显可见。这种交流电导率的弛豫现象在声发射活动较低时更为显著，而在短时间的锯齿波单轴加载实验中则未观察到（图 8-11B）。

8 复杂性在实验室地震学中的研究：从电学和声学发射到断裂

8.2.4 声发射与压力刺激电流的定量关联

为了关联压力激发电流和声发射技术的实验数据，可以采用不同的方法。由于固体中破裂过程产生的地震事件与记录到的声发射事件之间存在相似性，因此来自地震学领域的b值也可用于声发射事件的分析，依据以下修正的古滕贝格-里克特定律（科伦博等，2003）：

$$
\log_{10} N = a - b \frac{A_{dB}}{20}
\quad (8.2)
$$

其中 $N$ 是幅度高于 $A_{dB}$ 的声发射事件数量（或击中次数），$a$ 为恒定常数，$b$ 为声发射基础 $b$ 值，由公式 $(8.2)$ 所绘曲线的斜率计算得出。

或者，可以使用 $I_b$ 由塩谷等（1994）提出的所谓改进的b值代替公式(8.2)，以根据声发射分析中的幅值分布来描述固体断裂的各个阶段。改进的b值是利用幅值分布的统计值定义的，即平均值 $\mu$ 和标准差 $\sigma$，其关系如下（Shiotani et al., 1994）：

$$
I_b = \frac{\log N(\mu - \alpha_1\sigma) - \log N(\mu + \alpha_2\sigma)}{(\alpha_1 + \alpha_2)\sigma}
\quad (8.3)
$$

其中 $N(\mu - \alpha_1\sigma)$ 和 $N(\mu + \alpha_2\sigma)$ 分别表示振幅大于 $\mu - \alpha_1\sigma$ 和 $\mu + \alpha_2\sigma$ 的累计事件数。经验常数 $\alpha_1$ 和 $\alpha_2$ 由用户定义，通常设为1（Shiotani 等人，1994）。$I_b$ 变化的特征趋势可作为被测材料损伤程度的定性指标。当 $I_b$ 的值小于1时，表明微裂纹的产生和传播，因而与材料即将发生的破坏相关。

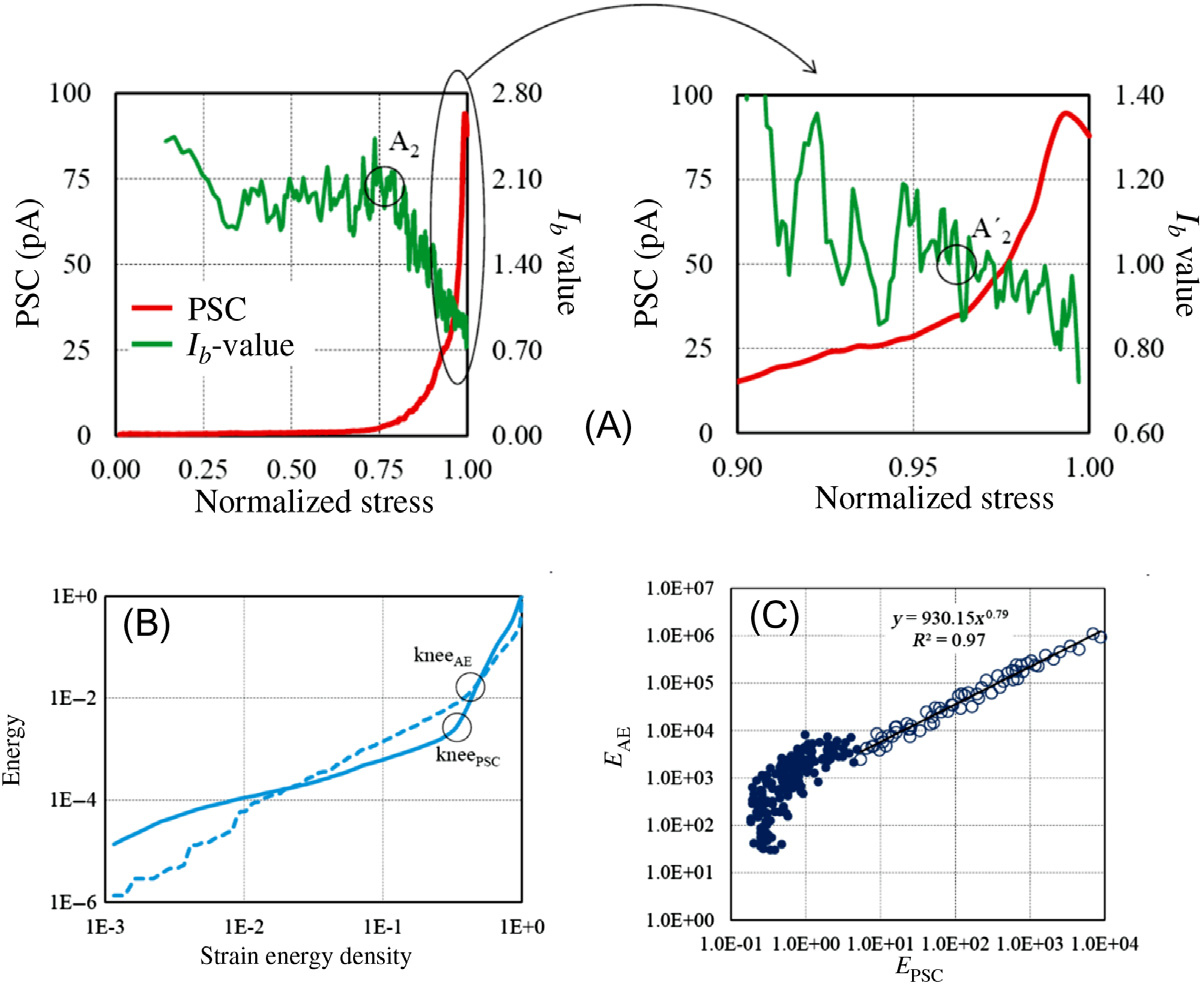
在 $I_b$ 值与大理岩试样单轴加载过程中压力刺激电流之间的相关性已由帕西乌和特里安蒂斯（2017）报告，并在Pasiou and Triantis(2017)中进行了说明图 8-12A。在应力达到最大应力的30%时，$I_b$ 值的初始下降归因于预先存在的微裂纹的闭合。由于微裂纹生成较少，$b$ 值在应力-应变偏离线性之前（B最大应力的80%）几乎保持恒定，但随后由于大量裂纹的形成，显著下降至接近1.0的数值（A 0 2点图 8-12A）。

在他们的研究中，Pasiou和Triantis还关联了多种脆性材料在压缩过程中声发射事件的能量与激发的压力刺激电流。对于压力刺激电流，释放的能量是通过以下关系计算的：

$$
E_{PSC} = \int_{t_i}^{t_i + \Delta t} \left(I_{PSC}(t)\right)^2 dt
\quad (8.4)
$$

其中积分是在时间间隔 $\Delta t$（$\Delta t = 1$ 秒）和 $t_i = 0; 1; …; n - 1$ 上计算的，$n$ 为实验的持续时间。一次声发射事件的绝对能量（以阿焦为单位）由声发射波形包持续时间内电压信号的平方对时间的积分除以10 kΩ参考电阻得到。

计算得到的大理石试样声发射事件和压力刺激电流的能量随应变能密度（SED）的变化如图 8-12B所示。SED是通过试验期间记录的应力-应变曲线下的面积计算得出的。两条曲线均包含两个近似直线段，其斜率不同，且在每种情况下均观察到一个拐点。值得注意的是，压力激发电流能量的拐点出现在声发射相应拐点之前，表明压电性电流技术对大理石试样内部损伤的检测更为敏感。声发射与压力激发电流能量在对数尺度上的相关性如图 8-12C所示。忽略压力激发电流能量大致保持恒定的范围（实心圆），在释放能量显著增加的区域（空心圆）适用幂律关系，即 $E_{AE} \sim (E_{PSC})^m$，其中 $m \approx 0.8$。

上述声发射和压力激发电流能量的相关性与瓦利安纳托斯和特里安蒂斯（2008）先前的研究一致，他们对大理岩进行了单轴应力试验，并对水泥砂浆试样进行了实验，并对记录的压力刺激电流事件间时间进行了统计分析，$\chi$（即连续压力激发电流事件之间的时间）。他们表明，相应的累积概率密度函数（PDF），$P(\chi)$，独立于断裂实验的类型（恒定应力或恒定应力率）以及材料种类（大理岩或水泥砂浆）。他们提出，该概率密度函数由其平均等待时间决定，并可由一种通用的缩放函数近似表示，该函数形式为伽马分布，即：$P(\chi) \sim \chi^{2-\gamma} \exp(-\chi/B)$，其中 $\gamma \approx 0.8$ 且 $B \approx 0.7$。他们得出结论，该函数与声发射和地震数据中观察到的函数非常相似，这意味着岩石断裂可能具有普适性，并在已进行的实验中至少跨越 3-4个数量级表现出自相似性。基于不可逆热力学，他们还描述了试样接近破坏时压力激发电流事件的累积能量随失效时间幂律的变化，类似于声发射数据和地震目录中观察到的现象（川田和永浜，2006；川田等，2007）。

在将PSC和电磁辐射技术应用于现场测量的框架下，压力刺激电压（PSVs）技术最近被引入（阿彻等，2016）。该技术基于萨塞克斯大学开发并取得专利的电位传感器（EPS）（普兰斯等，2000）。实验已证实，在各种岩石岩性中检测到的PSV来源于岩石本身，而非所用设备或局部环境（阿伊丁等，2009）。在同一项研究中，进行了单轴加载实验，以研究富石英正长花岗岩和非石英质盐岩中声发射事件与PSV活动之间的相关性。实验结果表明，声发射与PSV之间存在极强的正相关性。PSV的变化要么与相应的声发射记录同时被记录到，要么稍有延迟。作者认为，先于声发射（从而先于破裂）出现的PSV变化可能是由于应力累积，并发生在原子尺度上。这与前述的移动电荷位错机制是一致的。

8.3 岩石断裂复杂性与地震活动的相似性

8.3.1 察里斯熵基础：实验室地震学的统计力学方法

根据Tsallis (1988)提出的非广延统计物理，系统在离散情况下基于概率分布$p$的广义熵（塔萨利斯熵）$S_q$定义为：

$$
S_q = k_B \frac{1 - \sum_{i=1}^{W} p_i^q}{q - 1}; \quad q \in \mathbb{R} \quad \text{and} \quad \sum_{i=1}^{W} p_i = 1
\quad (8.5)
$$

其中，$k_B$ 是玻尔兹曼常数，求和表示系统可能状态的概率$p_i$的集合，总状态数为$W$。熵指数$q$表示系统非广延性的度量。当$q$趋近于1时，察里斯熵退化为经典统计物理中的玻尔兹曼-吉布斯（BG）熵。

对于由两个统计独立的子系统A和B组成的系统，塔萨利斯熵$S_q$违反了BG熵所遵循的可加性性质，具体表达式如下：

$$
S_q(A, B) = S_q(A) + S_q(B) + \frac{1 - q}{k_B} S_q(A)S_q(B)
\quad (8.6)
$$

等式右边最后一项公式(8.6)反映了所考虑的物理系统中由于长程相互作用导致的非可加性。指标 $q$ 的不同取值，即 $q > 1; q=1$ 和 $q < 1$ 分别对应次可加性、可加性和超可加性。

对于具有概率分布X的连续变量p(X)，公式(8.5)修改为：

$$
S_q = k_B \frac{1 - \int_0^N p^q(X)dX}{q - 1}
\quad (8.7)
$$

$X$变量可以是一个基本的地震参数，例如地震矩、连续两个事件之间的时间或事件间距离，这些事件例如是受力岩石内部产生的地震或微裂纹。

使察里斯熵 $S_q$ 优化的分布 $p(X)$ 受到自然约束，即归一化条件，

$$
\int_0^N p(X)dX = 1
\quad (8.8)
$$

以及关于广义期望值$X_q$（q‐期望值）的条件，其定义为：

$$
X_q = \langle X \rangle_q = \int_0^N X P_q(X)dX = 1
\quad (8.9)
$$

其中 $P_q(X)$ 是来自以下表达式的伴随概率（察里斯，2009）：

$$
P_q(X) = \frac{p^q(X)}{\int_0^N p^q(X)dX}
\quad (8.10)
$$

通过拉格朗日乘数，我们最终得到物理概率：

$$
p(X) = \frac{[1 - (1 - q)\beta_q X]^{1/(1 - q)}}{Z_q}
\quad (8.11)
$$

在上述方程中，分子表示q‐指数函数$\exp_q(-\beta_q X)$，其定义为：

$$
\exp_q(X) =
\begin{cases}
[1 + (1 - q)X]^{1/(1 - q)} & \text{for } 1 + (1 - q)X \geq 0 \
0 & \text{for } 1 + (1 - q)X < 0
\end{cases}
\quad (8.12)
$$

公式(8.11)中的分母是q‐配分函数

$$
Z_q = \int_0^{X_{\text{max}}} \exp_q(-\beta_q X) dX
\quad (8.13)
$$

其中，项 $\beta_q$ 与拉格朗日乘子 $\beta^*$ 的关系如下：

$$
\beta_q = \frac{\beta^*}{c_q + (1 - q)\beta \langle X \rangle_q} \quad \text{and} \quad c_q = \int_0^{X_{\text{max}}} p^q(X)dX
$$

通过考虑q‐指数的分布，而非单一的q值，可以进一步推广非广延统计物理的先前标准表示形式，正如Tsallis(1988)和Tsekouras 和 Tsallis (2005)所提出的。在这种情况下，引入一个广义微分方程来描述在变量X较大时观察到的向另一种行为类型的交叉，如下所示：

$$
\frac{dp}{dX} = -\beta_r p^r - (\beta_q - \beta_r)p^q
\quad (8.14)
$$

在 $r=0$ 或 $r = q$ 的平凡情况下，方程(8.14) 简化为非线性微分方程$dp/dX = - \beta_q p^q$，其解为广义概率 $p(X)$，由 公式(8.11) 给出。当 $1 \leq r < q$ 时，方程(8.14) 的通解如下所示：

$$
X = \int_p^1 \frac{dx}{\beta_r x^r + (\beta_q - \beta_r)x^q} = \frac{1}{\beta_r} \int_p^1 dx \left[ \frac{1}{x^{r-1}} - \frac{\beta_q/\beta_r - 1}{x^{q-2r-1}} - \frac{\beta_q/\beta_r - 1}{x^{q-r-1}} \right]
$$

这最终导致：

$$
X = \frac{1}{\beta_r} \left{ \frac{p^{1-r} - 1}{r - 1} - \frac{\beta_q/\beta_r - 1}{1 + q - 2r} H(1; q - 2r; q - r; \beta_q/\beta_r - 1) - H(p; q - 2r; q - r; \beta_q/\beta_r - 1) \right}
\quad (8.15)
$$

其中

$$
H(\xi; a; b; c) = \xi^{1+a} F\left(1 + \frac{a}{b}; 1; 1 + \frac{a + b}{c}; -\xi^{bc}\right)
$$

而$F$是超几何函数。

在将非广延统计物理应用于各种系统时，出现的问题是我们应该将所考虑系统的分布与哪种分布进行比较。如果使用的是escort分布，而不是p(X)（如公式(8.11)中给出的物理概率），那么我们将得到以下累积分布函数(CDF)：

$$
P_{\text{cum}}(X) = \int_{X_{\text{min}}}^{\infty} P_{\text{esc}}^q(X)dX = \exp_q(-X/X_0)
\quad (8.16)
$$

或者，通过对物理概率p(X)进行积分，在适当变换后可得到以下累积概率（Michas 等人, 2013）：

$$
P(X) = 1 - (1 - q) \left(\frac{X}{X_0}\right)^{(2 - q)/(1 - q)}
\quad (8.17)
$$

通过优化变量$X^2$的平方的察里斯熵$S_q$，可以得到著名的高斯分布的一种广义形式。因此，我们得到如下q‐高斯分布：

$$
p(X) = p_0 \left[1 - (1 - q) \left(\frac{X}{X_0}\right)^2 \right]^{1/(1 - q)}
\quad (8.18)
$$

当 $q \to 1$ 时，得到标准高斯分布；而当 $q > 1$ 时，q‐高斯分布的尾部遵循幂律，从而提高了 $X$（图 8-14）中高值出现的概率。

8.3.2 实验室实验中的应用

最近，已开展多项研究以探讨非广延统计物理在受力岩石声发射和压力刺激电流实验室尺度实验中的适用性（瓦利安纳托斯 等，2011，2012a,b,c，2013a,b；瓦利安纳托斯和特里安蒂斯，2012，2013；Cartwright-Taylor 等人，2014）。值得注意的是，非广延统计物理的概念还已被扩展到板块构造和全球地震活动等大规模系统（瓦利安纳托斯和萨蒙兹，2010，2011，2013）。

在NESM框架内，从现象学角度研究了KTB钻孔细粒角闪岩岩石在受到高速应力阶跃作用时记录的压力刺激电流的弛豫行为（瓦利安纳托斯和特里安蒂斯（2012））。在他们的实验中，每个岩石试样均受到高应力率（约3兆帕/秒）的阶跃式单轴应力作用，并达到不同的高恒定应力值$\sigma_H$。在每种情况下，压力刺激电流都被记录了足够长的时间，以观察当应力在特定阶跃达到其高值后，在最大电流发射之后的弛豫信号。他们观察到量 $\xi(t)$，定义为压力刺激电流弛豫信号$I(t)$除以在每个阶跃中记录的最大电流$I_o$（即$\xi(t) = I(t)/I_o$），随时间单调递减，在$\sigma_H$较低时遵循指数规律，即 $\xi(t) = \exp(-\beta_1 t)$。然而，当$\sigma_H$超过屈服应力时，在中间时间范围观察到向幂律的偏离，特别是在$\sigma_H$接近断裂应力时更为明显。

这种偏离与记录的弛豫电流的分形图像相关，可用广义q‐指数函数 $\xi(t) \sim \exp_q(-\beta_q t)$描述，该函数定义于公式(8.12)中。根据q‐指数函数对实验数据拟合的曲线在图 8-15中以绿色显示，适用于 $\sigma_H > \sigma_Y$的情况。然而，考虑到在高施加应力下实验数据在极长时间偏离幂律行为，瓦利安纳托斯和特里安蒂斯提出了以下微分方程，用于描述在极长时间下向另一种行为类型的交叉：

$$
\frac{d\xi(t)}{dt} = -\beta_1 \xi - (\beta_q - \beta_1)\xi^q
\quad (8.19)
$$

该方程是广义的方程(8.14)在$r=1$时的特例，其解为：

$$
\xi(t) = \left[1 - \frac{\beta_q}{\beta_1} + \frac{\beta_q}{\beta_1} \exp((q - 1)\beta_1 t)\right]^{-1/(q - 1)}
\quad (8.20)
$$

如图 8-15所示，使用公式(8.20)对压力激发弛豫电流进行拟合，在整个时间范围内表现出非常好的相关性。

在同一框架下，非广延统计物理也被应用于同一作者对之前实验的改进集（瓦利安纳托斯和特里安蒂斯，2013），他们研究了在连续加载-卸载循环下大理岩和角闪岩样品中发射的压电传感器信号。他们观察到，与之前的结果一致，归一化的PSC弛豫信号，$\xi(t)$，在大理岩和角闪岩样品中均偏离指数行为，表现出广义的q‐指数函数$\exp_q(-\beta_q t)$在长时间范围内的幂律特性（见瓦利安纳托斯和特里安蒂斯，2013中的图2）。在五个连续循环的每一次加载-卸载循环中，与PSC弛豫相关的察里斯q‐参数随着连续循环次数的增加而逐渐减小，趋近于$q=1$的值（图 8-16）。这表明，描述裂缝网络的分布通过重复加载-卸载循环逐渐趋向于普通指数，暗示了一个具有层次约束动力学的次可加性破裂过程。他们得出结论：在NESP框架下对PSC弛豫函数的描述揭示了源自驱动发射弛豫电流的裂缝网络的分形图像。

在他们的研究中，还采用了一种互补的方法，即所谓的超统计，来探究将非广延统计物理应用于PSC弛豫宏观行为的动力学原因。在这种方法中，考虑了一个由大量弛豫子域组成的简单模型，局部弛豫由德拜指数弛豫$\xi(t|\beta) = \beta e^{-\beta t} = (1/\tau)e^{-t/\tau}$表示。对于某个特定的局部弛豫参数 $\beta$，一个子域的弛豫为 $\xi(t|\beta)$。观测到的PSC弛豫信号是这些由复杂裂缝网络构成的子域弛豫的宏观结果，因此系统的弛豫强度参数 $\beta$ 应在很大范围内波动。这一假设导致了对指数模型的超统计观点。他们考虑了$\chi^2$‐分布作为 $\beta$的概率密度函数，如下所示

$$
f(\beta) = \left(\frac{z}{2\beta_0}\right)^{z/2} \frac{\beta^{(z/2)-1}}{\Gamma(z/2)} \exp\left(-\frac{z\beta}{2\beta_0}\right)
\quad (8.21)
$$

导致弛豫函数

$$
\xi(t) = \int_0^\infty f(\beta)\xi(t|\beta)d\beta = \int_0^\infty f(\beta)\beta e^{-\beta t}d\beta = \left[1 + B(q - 1)t\right]^{1/(1 - q)}
\quad (8.22)
$$

这正是在NESP框架内得到的结果，其中 $q = 1 + 2/(z - 1)$ 和 $B = 2\beta_0/(2 - q) = \beta_q$。

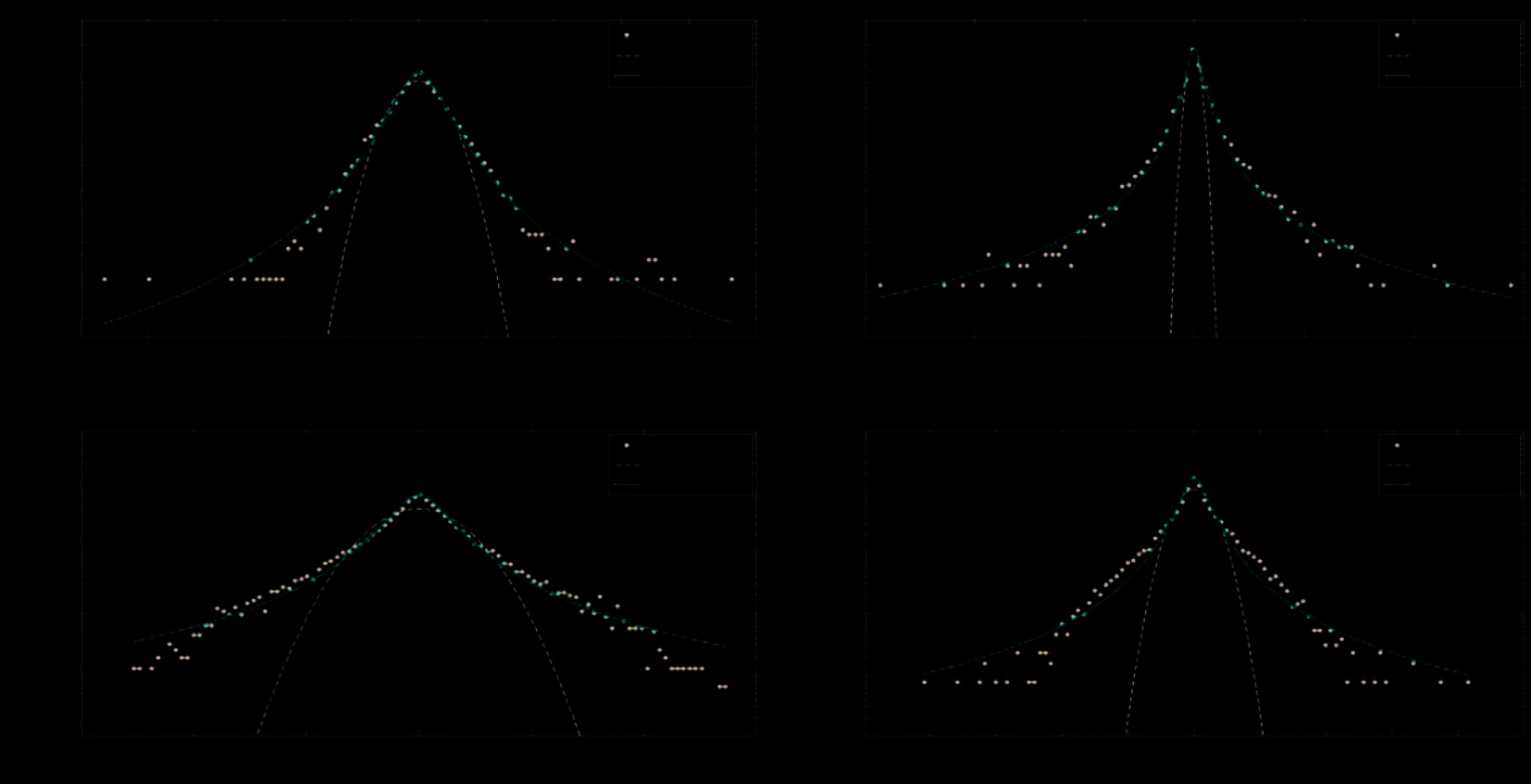
最近，Cartwright-Taylor et al.(2014)报道了三轴变形卡拉拉大理石试样中应力诱导电流波动的超统计观点。在其变形实验中，针对PSC波动的非广延行为进行了研究，该波动由变量$u_i = (F_i - \langle F \rangle)/\sigma_F$描述，其中$F_i = I(t_{i+1}) - I(t_i)$表示增量压致电波动，而$\langle F \rangle$、$\sigma_F$代表平均值和标准差，分别地。归一化增量$p(u)$的$u(t)$在不同围压下的概率密度函数（PDF）如图8-17所示。在所有围压条件下，分布均可用非广延q‐高斯函数描述，其q参数范围从30 MPa时的1.53到100 MPa时的1.78。作者将观察到的q值变化解释为：随着破坏模式从局部化的脆性断裂（P < 30 MPa）转变为具有均匀分布微裂纹的碎裂流机制（P > 30 MPa），长程相互作用增强所致。

将超统计概念应用于先前的PSC波动，导致出现q‐高斯分布，这是由于PDF的 $\beta$参数[发生变化所致，参见公式(8.21) 和 (8.22)]，该分布描述了系统在短时间尺度下的行为。当 $\beta$的变化时间尺度远大于$u(t)$的时间尺度时，$u(t)$的PDF可表示为临时平衡态的叠加。在局部平衡条件下，若 $\beta$被视为恒定，则$u(t)$的PDF可近似为

$$
p(u|\beta) = \sqrt{\frac{\beta}{2\pi}} \exp\left(-\frac{\beta}{2} u^2\right)
\quad (8.23)
$$

而 ，如果 $\beta$在更长的时间尺度上波动，则$u(t)$的分布由

$$
p(u) = \int p(u|\beta)f(\beta)d\beta
\quad (8.24)
$$

作者考虑使用 $\Gamma$‐分布来描述 $\beta$的稳态分布，

$$
f(\beta) = \frac{1}{\Gamma(\alpha)} \left(\frac{\alpha}{\beta_o}\right)^\alpha \beta^{\alpha-1} \exp\left(-\frac{\alpha\beta}{\beta_o}\right)
\quad (8.25)
$$

得到一个概率密度函数，$p(u) \sim (1 + B(q - 1)u^2)^{-1/(q - 1)}$，其形式为q‐高斯分布。

非广延统计物理（NESP）的概念也被应用于埃特纳玄武岩三轴变形试样的声发射数据中（瓦利安atos 等, 2012a,b,c）。实验在高度破碎的非均质脆性材料样品（来自意大利埃特纳火山的玄武岩）上进行，在不同围压下以恒定的轴向应变率加载。实验连续监测了声发射活动的空间和时间演化，并高精度估算了扩展裂纹的定位模式。在他们的研究中，分析了声发射标量矩 $M$ 的累积分布函数 $P(>M)$，声发射事件间时间 $P(>T)$ 以及声发射事件间欧氏距离 $P(>D)$ 的累积分布函数。在每种情况下，累积分布函数（见 公式 8.16）应满足以下关系：

$$
\frac{P_{1-q}(>X) - 1}{1 - q} = -BX
\quad (8.26)
$$

其中方程的左侧是q‐对数函数，$\ln(P(>X))$。根据公式 (8.26)，标量矩M的q指数估计为$q_M = 1.82$，与其他关于地震和其他自然灾害的q值估计一致。因此，声发射事件间时间与距离的q指数分别估计为$q_T = 1.34$ 和 $q_D = 0.65$。后者表明，由事件间时间与距离描述的声发射活动表现出非广延时空对偶性（$q_T + q_D \approx 2$），类似于在地球地震活动中观察到的现象（Abe 和 Suzuki, 2003, 2005）。

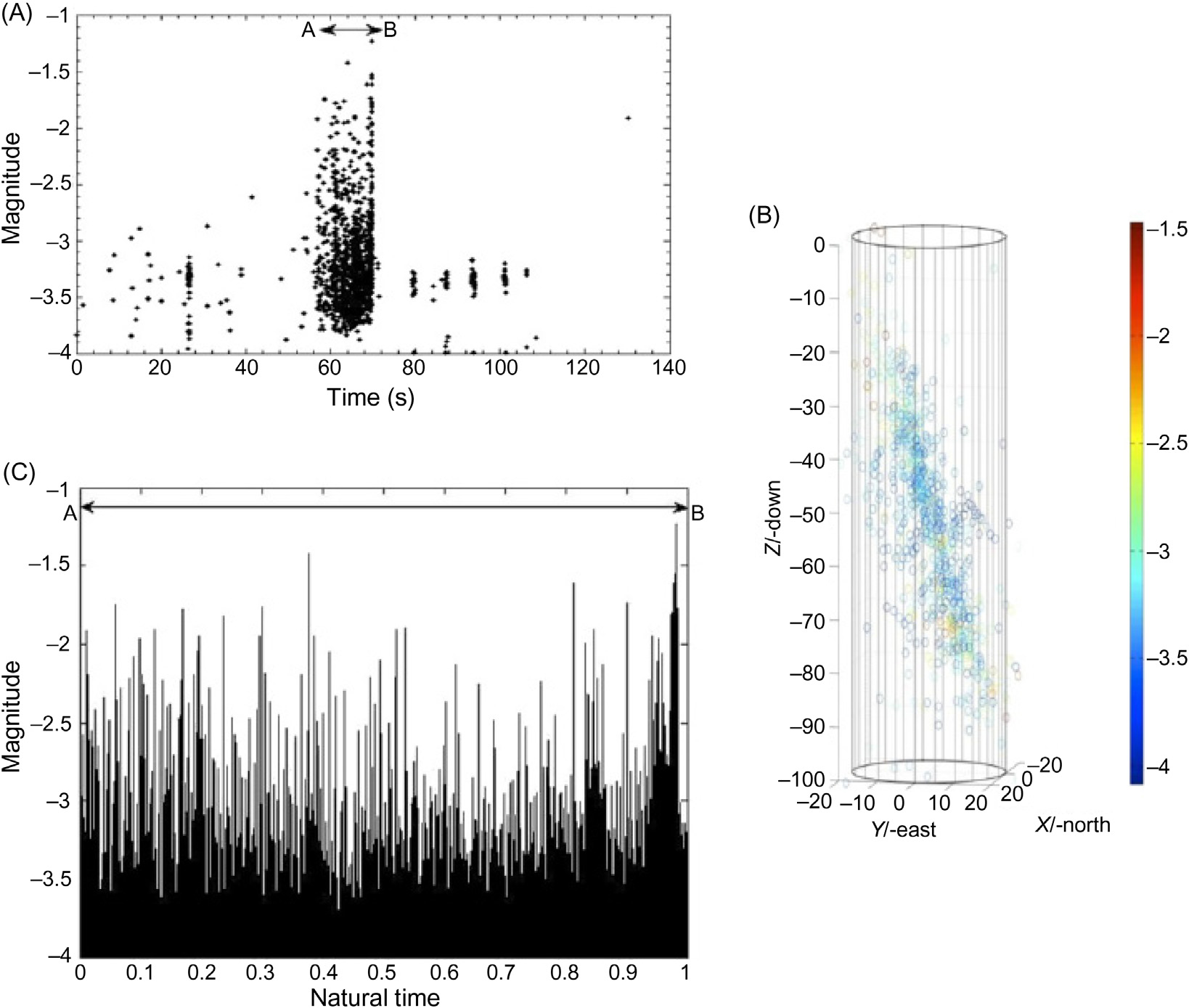
8.3.3 自然时间分析

为了研究声发射和压力激发电流信号与岩石破裂过程的相关性，并从早期加载阶段估计断裂的载荷水平，复杂性技术可能具有前景（Hloupis 等, 2016）。最近，自然时间分析被引入用于描述复杂系统的动态演化及其进入临界状态的过程（Varotsos 等, 2001, 2002, 2011a,b；瓦利安托斯等人，2012a,b,c，2013a,b；Hloupis 等, 2015）。

在记录的 $N$个声发射事件的时间序列中，自然时间 $\chi$定义为 $\chi_k = k/N$，用作第 $k$个事件发生顺序的索引（图 8-18A和 B）（Varotsos 等, 2011a）。在考虑声发射分析中第 $k$个事件释放的地震矩$M_k$ 时，连续函数 $F(\omega)$定义为（Varotsos 等,2011a,b）：

$$
F(\omega) = \sum_{k=1}^{N} M_k \exp\left(i\omega \frac{k}{N}\right)
\quad (8.27)
$$

其中 $\omega = 2\pi\phi$，且 $\phi$ 对应于固有频率。

The归一化函数，$\Phi(\omega)$通过将 $F(\omega)$ 除以 $F(0)$ 得到，如下所示 :

$$
\Phi(\omega) = \frac{\sum_{k=1}^{N} M_k \exp(i\omega k/N)}{\sum_{n=1}^{N} M_n} = \sum_{k=1}^{N} p_k \exp\left(i\omega \frac{k}{N}\right)
\quad (8.28)
$$

其中 $p_k (= M_k/\sum_{n=1}^{N} M_n)$ 对应于在自然时间观察到第 $k$个声发射事件的概率，即 $\chi_k$。随后，公式(8.28)的归一化功率谱，定义为 $\Pi(\omega) = |\Phi(\omega)|^2,$，对于 $\phi < 0.5$:

$$
\Pi(\omega) = \frac{18}{5\omega^2} - \frac{6 \cos\omega}{\omega^2} - \frac{12 \sin\omega}{5\omega^3}
\quad (8.29)
$$

根据概率论，如果已知分布函数在零附近的性态，则可近似确定该分布函数。因此，当 $\omega \to 0$ 时，公式(8.29) 导出

$$
\Pi(\omega) \approx 1 - \kappa_1 \omega^2
\quad (8.30)
$$

其中系数 $\kappa_1$ 是自然时间的方差，表示为 :

$$
\kappa_1 = \langle \chi^2 \rangle - \langle \chi \rangle^2 = \sum_{k=1}^{N} p_k \chi_k^2 - \left(\sum_{k=1}^{N} p_k \chi_k\right)^2
\quad (8.31)
$$

研究表明，当一个复杂系统接近临界状态时，参数$\kappa_1$应趋近于值 $\kappa_1 = 0.07$（Varotsos 等，2011b）。不同参数 $\kappa_1$取值下的归一化功率谱 $\Pi(\phi)$已在 图 8-18C中绘制。

Vallianatos 等(2013a,b)在自然时间背景下研究了埃特纳玄武岩三轴变形试样中的声发射活动（图 8-19）。声发射幅度作为的时间函数

时间显示在图 8-19A中。在变形的最后阶段观察到显著的声发射活动，该区域标记为图 A中的 8-19B。对该时间段内的声发射数据进行了自然时间域分析（见图 8-19C）。为了根据以下关系式计算概率$p_j$的平均值，对声发射目录中的$W$个事件采用了滑动自然时间窗（长度为$l$，起始点为$k_0$）：

$$
\mu_j = \frac{1}{W - l + 1} \sum_{k_0=1}^{W-l+1} \frac{M_{k_0 + j - 1}}{\sum_{m=1}^{l} M_{k_0 + m - 1}}
\quad (8.32)
$$

随后，从声发射目录的 $W - l + 1$ 个时间窗口中获得的参数 $\kappa_1$ 的期望值表示为：

$$
E(\kappa_1) = \kappa_{1,M} + \sum_{j=1}^{l-1} \sum_{i=j+1}^{l} \frac{(j - l)^2 - l^2}{Cov(p_j, p_i)}
\quad (8.33)
$$

其中 $\kappa_{1,M}$由 公式 (8.31) 得到，通过将 $\mu_k$代入$p_k$，而$Cov(p_j,p_i)$是$p_j$的协方差。为了识别自然时间基准下声发射幅度相关性的存在，类似于区域尺度地震活动，他们将原始声发射时间序列的$\kappa_1$的期望值$E(\kappa_1)$与$E(\kappa_{1, \text{shuf}})$的分布进行比较，其表达式为：

$$
E(\kappa_{1, \text{shuf}}) = \kappa_u \left(1 - \frac{1}{l^2}\right) + \frac{1}{l + 1} \text{Var}(p)
\quad (8.34)
$$

当使用多个原始声发射数据集的随机打乱副本时。在上述方程中，$\kappa_u$对应于均匀分布，$\text{Var}(p)$是打乱后的目录中的方差。他们发现$E(\kappa_{1, \text{shuf}})$服从正态分布（$\mu_s = 0.0573$；$\sigma = 0.00097$），而原始声发射目录得到的平均$\kappa_1$值（$\mu_0 = 0.0614$）不太可能来自此分布。这归因于$\mu_0$与原始声发射目录中长程相关性的存在有关。

值得注意的是，基于自然时间中序参量$\kappa_1$的统计特性，他们还发现其声发射目录与 1900-2007时期的百年地震目录具有相似性，表明声发射与全球地震活动性之间存在普适性。他们认为，在实验室尺度下压缩岩石试样中形成的剪切带的演化过程，与宏观尺度下的剪切过程（如断层带）的演化非常相似。

最近，一项实验方案被应用于对采自希腊阿提卡狄俄尼索斯山的大理岩制成的双刃缺口拉伸(DENT)试样进行声发射和PSC测量（Kourkoulis 等，2017）。通过声发射技术和 PSC技术同时监测试样的力学响应和断裂行为。此外，采用数字图像相关（DIC）技术确定所发展的位移场，并借助超高频高速相机捕捉裂纹的起始与扩展过程。同时，使用引伸计测量缺口张开位移，主要用于比较与标定目的。所使用的复杂传感系统的主要优势在于，它们能够提供来自试样表面以及内部的数据。该项工作的目的是研究早期检测大理岩结构元件即将发生灾难性断裂的问题。实验数据在以下假设框架下进行研究：复杂系统的独特且隐藏的力学特征可以通过测量时间序列来检测，并以自然时间进行分析（Varotsos 等，2011a,b；Vallianatos 等，2013a,b, 2014；Hloupis 等，2015）。在这一初步研究中，指示即将发生临界状态的力学特性结果与应用自然时间分析后的相应结果进行了对比。在先前发表的一项研究中（Hloupis 等，2015），表明声发射分析可提供有关临界性逼近的信息。具体而言，将量值RA（上升_时间/幅度）作为输入引入自然时间场。一个显著的观察结果是，在所有测试实验中，自然时间分析均能揭示一个临界点（进入‘临界阶段’的入口点）。具体来说，$\kappa_1$参数的研究采用了从靠近断裂区布置的声发射传感器获取的声发射事件计算得到的RA量值作为输入（Varotsos 等，2011a,b；Vallianatos 等，2013b, 2014；Hloupis 等，2015）。自然时间分析揭示了指示进入‘临界阶段’的指标（见图8a-d，Hloupis 等，2015）。一个有趣的观察结果是，接近临界点的时间（临界性起始时间）在所有声发射记录通道中并不相同。对此的详细解释可在Hloupis 等（2015）中找到。本研究取得的令人鼓舞的结果证明了NT方法的稳健性，因为独立事件数量$N$（在自然时间术语中即本研究中记录的声发射事件数）并未影响该方法的适用性。由于上述实验中的主要问题之一是确定裂纹起始位置，因此对每组声发射传感器分别考察了进入临界状态的情况。需要注意的是，一对声发射传感器放置在试样左侧缺口附近，另一对声发射传感器放置在试样右侧缺口附近。据此，提供了试样左右两侧满足临界条件的相对时间，从而可以确定临界性起始顺序。除了存在指示进入临界阶段的临界点外