第十二届蓝桥杯B组省赛部分真题

原创已于 2023-04-02 20:24:26 修改 · 166 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #c++ #算法

于 2023-03-26 20:40:40 首次发布

C++ 专栏收录该内容

4 篇文章

订阅专栏

文章介绍了两道编程题的解决方案，第一题通过优化暴力求解，利用约数找货物摆放方式；第二题使用DFS和动态规划(DP)求解砝码称重问题，展示了从深度优先搜索到状态转移矩阵的优化过程。

试题D：货物摆放

看到题目首先想到用暴力的方法去求解，三个for循环去求解，但是n位一个16位数值，直接暴力肯定会时间超限的，于是我们得想方法优化它，不能想到可以只写两个for循环，全排列出前两个数，第三个数通过n=L*W*H的公式变换为H=n/W/H去确定第三个未知数。但是，还是超限。继续思考优化的点，暴力还是不太可行，可以发现，因为n=L*W*H，故L和W和H都为n的约数，这样只要我们把n的约数求出来（一共才百来个），再在这些约数中暴力求解即可。

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;

// 求约数
vector<long long> get_divisors(long long n)
{
    vector<long long> divisors;
    // 减少循环次数
    long long t = sqrt(n);
    for (long long i = 1; i <= t; i++)
    {
        // 能整除说明为一个约数，则有一个与之对应的约数 n/i
        if (n % i == 0)
        {
            divisors.push_back(i);
            if (i != n / i)
                divisors.push_back(n / i);
        }
    }
    return divisors;
}
int main()
{
    long long n, ans = 0;
    cin >> n;

    vector<long long> vec = get_divisors(n);
    for (int i = 0; i < vec.size(); i++)
        for (int j = 0; j < vec.size(); j++)
            if (n % (vec[i] * vec[j]) == 0)
                ans++;
    cout << ans << endl;

    system("pause");
    return 0;
}

试题G：砝码称重

考点

DP动态规划、DFS（骗分）

题解

解法1 DFS（50%）

#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <set>

using namespace std;

int n, w[110], flag[110];
set<int> ans;
void dfs(int sum1, int sum2)
{
    // 两种对称情况，剪枝即可
    if (sum1 < sum2)
        return;
    // 根据set结构的特性插入可能的结果
    else if (sum1 > sum2)
        ans.insert(sum1 - sum2);
    for (int i = 1; i <= n; i++)
    {
        if(!flag[i])
        {
            // 标记已经被选择过了
            flag[i] = 1;
            // 进行dfs深搜，将砝码选中放到左边
            dfs(sum1 + w[i], sum2);
            // 将砝码选中放到右边
            dfs(sum1, sum2 + w[i]);
            // 回溯标记
            flag[i] = 0;
        }
    }
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> w[i];
    dfs(0, 0);
    cout << ans.size();

    system("pause");
    return 0;
}

解法2 dp

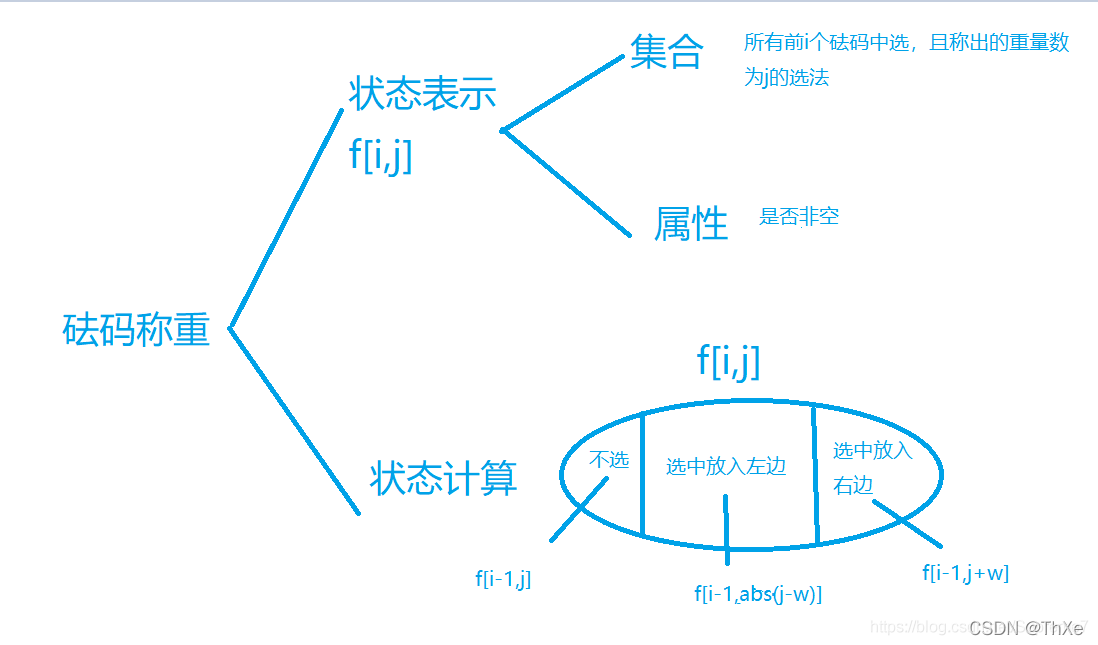
一般来说能够深搜的题且是求方案数的都可以用DP来优化，这题就是最好的例证。（引用别人的图）

#include <iostream>
#include <algorithm>
#include <cmath>
#include <string>
#include <set>

using namespace std;

// 一维为第几个砝码，二维为重量
bool dp[110][200010];
int main()
{
    int n, w[110] = {}, ans = 0, sum = 0;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i];
        sum += w[i];
    }
    // 初始化
    dp[0][0] = true;
    for (int i = 1; i <= n; i ++)
        for(int j = 0; j <= sum; j++)
        // 考虑第 i 个的情况，分别为不选中该砝码，放入左边天平和放入右边
            dp[i][j] = dp[i-1][j] || dp[i-1][j+w[i]] || dp[i-1][abs(j-w[i])];
    for (int i = 1; i<=sum; i++)
        if (dp[n][i])
            ans ++ ;
    cout << ans;
    system("pause");
    return 0;
}