蓝桥刷题小结

P8783 [蓝桥杯 2022 省 B] 统计子矩阵

题解：本题要求子矩阵，如果使用遍历循环去求解子矩阵中的元素之和肯定是超时的。这个时候我们很容易想到使用前缀和去优化求解元素之和的问题，在二维矩阵中又叫二维前缀和。在矩阵中，需要确定一个矩阵需要一个左上角顶点和一个右下角的顶点。二维前缀和求解的矩阵为从sum[i][j]的表现形式，解释为左上角顶点为（1，1）、右下角为（i，j）的顶点所组成的矩阵内的元素之和。

二位前缀和求解公式：sum[i][j] = sum[i-1][j] + prefixSum（一维前缀和）；

#include <iostream>
#include <cstdio>

using namespace std;

long long sum[510][510] = {};
int n, m, k, a[510][510] = {}, ans = 0;
int main()
{
    scanf("%d %d %d", &n, &m, &k);
    // 求解二维前缀和
    for (int i = 1; i <= n; i++)
    {
        int prefixSum = 0;
        for (int j = 1; j <= m; j++)
        {
            // cin >> a[i][j];
            scanf("%d", &a[i][j]);
            prefixSum += a[i][j];
            sum[i][j] = sum[i - 1][j] + prefixSum; 
        }
    }
    // 循环遍历求解答案，但这样暴力去循环只能拿80的分数，想ac还得进行优化
    for (int x1 = 1; x1 <= n; x1++)
        for (int y1 = 1; y1 <= m; y1++)
            for (int x2 = x1; x2 <= n; x2++)
                for (int y2 = y1; y2 <= m; y2++)
                    // 这一大串代表的是（x1，y1）到（x2，y2）的矩阵内元素之和
                    if (k >= sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1])
                        ans ++ ;

    cout << ans;

    system("pause");
    return 0;
}

 P8780 [蓝桥杯 2022 省 B] 刷题统计

 简单题，记录一下忘记开long long了，看到数据范围的时候想起要加long long的，等头文件写上去的时候就忘记了。

P8785 [蓝桥杯 2022 省 B] 扫雷

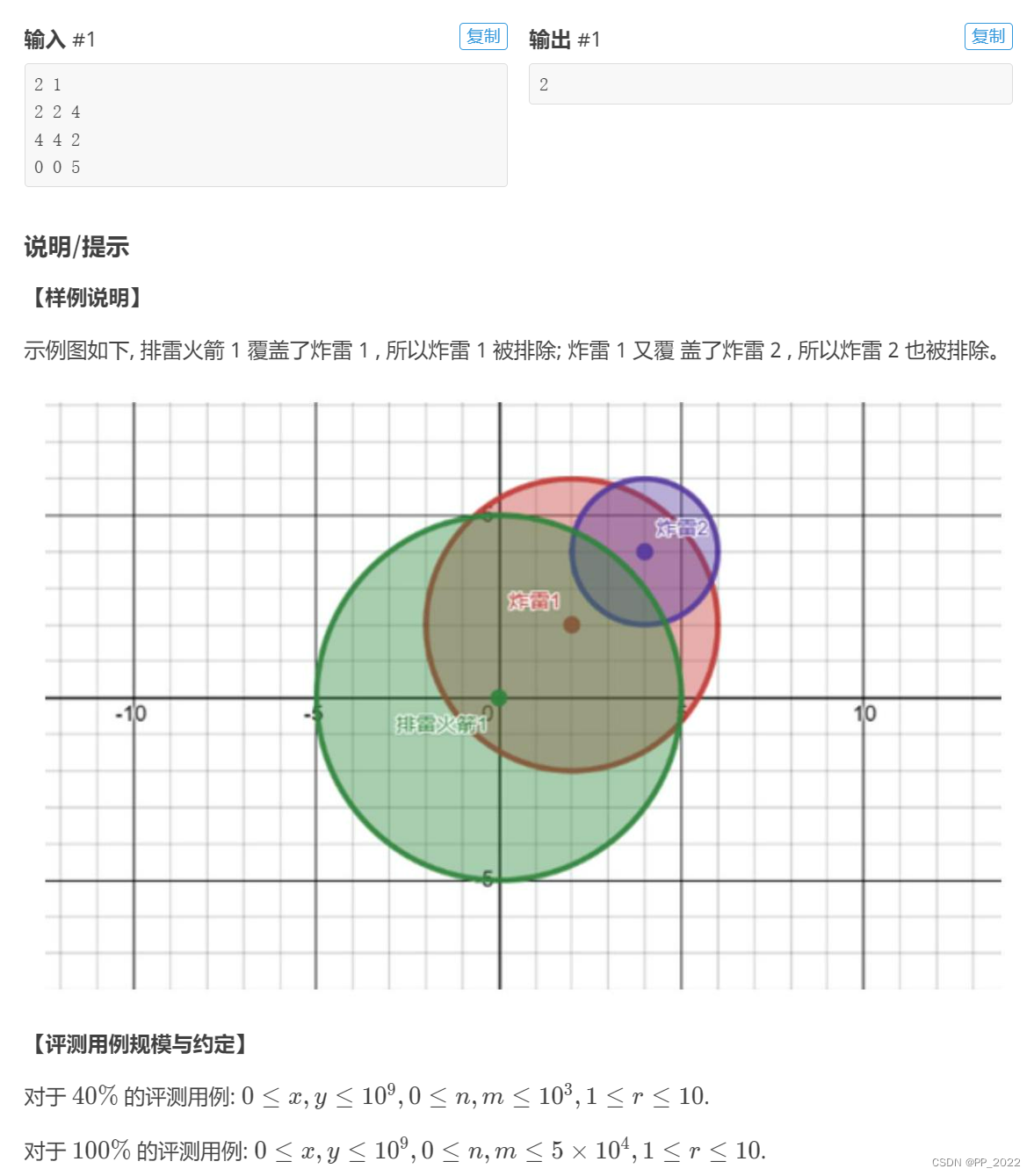
题解：本题不清楚排雷火箭到底可以引爆多少个的炸弹，所以只能使用 dfs 进行搜索遍历查找，但是直接遍历的话，根据本题的一个数据范围，时间肯定会超出限制。所以需要 dfs 的剪枝优化。观察题目可以发现，本题的 x 和 y 的范围非常的大但是 r 爆炸半径却很小，所以有很多炸弹都不会被一个火箭所涉及，如果去直接进行遍历的话大大浪费了时间。而我们发现，只要两个点的 x 轴相差的距离大于 r 那么不管这两个点的 y 值为多少，它们之间的距离必定大于爆炸半径 r 。通过对 x 范围的二分查找进行剪枝。

#include <iostream>
#include <cmath>
#include <algorithm>

using namespace std;

// 定义炸弹结构体，flag为是否引爆过
struct zha
{
    int x, y, r;
    bool flag;
} a[50010];
// 定义排雷火箭结构体
struct
{
    int x, y, r;
} b[50010];
// 结构体快排升序排列
bool cmp(zha a, zha b)
{
    return a.x < b.x;
}
int n, m, ans;
// 计算两点之间的距离
double getDistance(int x1, int y1, int x2, int y2)
{
    int x = x1 - x2, y = y1 - y2;
    return sqrt(x * x + y * y);
}
// 通过dfs深搜，通过二分确定左右边界减少循环次数剪枝
void dfs(int x, int y, int r)
{
    int left = 1, right = n, mid, L, R;
    // 二分确定左边界
    while (left <= right)
    {
        mid = (left + right) / 2;
        if (a[mid].x < x - r)
            left = mid + 1;
        else
            right = mid - 1;
    }
    L = left;
    right = n;
    // 二分确定右边界
    while (left <= right)
    {
        mid = (left + right) / 2;
        if (a[mid].x <= x + r)
            left = mid + 1;
        else
            right = mid - 1;
    }
    R = left;

    // 根据左右边界进行剪枝，在边界内循环
    for (int i = L; i < R; i++)
    {
        if (!a[i].flag && getDistance(x, y, a[i].x, a[i].y) <= r)
        {
            a[i].flag = true;
            ans++;
            dfs(a[i].x, a[i].y, a[i].r);
        }
    }
}

int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d %d %d", &a[i].x, &a[i].y, &a[i].r);
    for (int i = 1; i <= m; i++)
        scanf("%d %d %d", &b[i].x, &b[i].y, &b[i].r);
    // 进行快排，方便待会进行二分查找
    sort(a + 1, a + 1 + n, cmp);

    for (int i = 1; i <= m; i++)
        dfs(b[i].x, b[i].y, b[i].r);
    cout << ans << endl;

    system("pause");
    return 0;
}