trie树+思维 Xor-MST

Xor-MST

大意：

思路：

先讲一下我自己一开始的思路吧：嗯...两两之间都有边...嗯?是对应的异或值？？？...trie树？？？...不对...最小生成树？...emmm可这也转化不到kruskal啊...摆了摆了...

关于MST，Boruvka算法告诉我们，对于每一个连通块，每次向外伸出一条最短的边并连接，这样操作最后就能得到一颗最小生成树，并且由于每次至少消掉一半的连通块，所以复杂度是吃得住的。放到这一题里来的话，对于每一个连通块，我们很难快速找到其对应的最小边。这时就有一个神奇的思路。

我的一开始的思路其实是ok的，就是trie，毕竟关于异或的题，很多都可以跟trie扯上关系。如果我们将所有数字的二进制表示放到trie上面去的话，不难发现，所有二进制串的结尾都是数的叶子节点，这是因为如果有两个数字的二进制串长度不同，在从高位往低位建树的过程中，缺失的部分会自动补上0.

比如我们来模一下样例：

                         

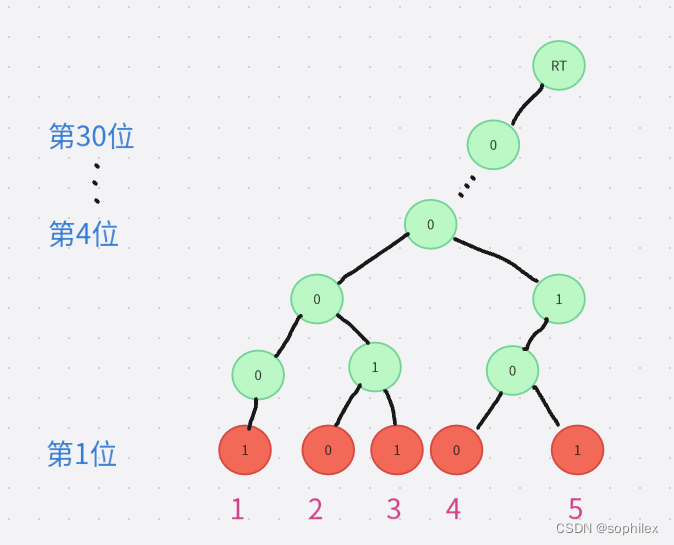
既然如此，那么任意两个数字之间的异或值就是它们到根节点路径上的对应节点的异或值的累加，那么我们就不难发现，trie树上两个叶子节点的lca深度越深，它们的异或结果也就越小。另外考虑到这里其实每一个叶子节点就对应一个连通块，并且每一个有两个儿子的节点，他的两个子树连通块一定是相互独立的，换句话说，我们一定需要从这两个连通块里找到两个异或值最小的数字才能将这两个连通块合并。而最后得到一个最小生成树，也就是对于每一个有两个儿子的节点都要进行一次在子树里选择的过程，都选择完之后，题目也就解决了。

另外，如果我们将数字按顺序插入trie树中，那么每一个节点对应的范围也就是原序列里一段连续的区间了，那么我们就可以很轻松地每次去查找两个子树合并的最小代价了，只要遍历左子树对应的数字，然后在右子树里找到它的最小异或值就好了。当然反一下也是可以的。

具体来说，从上向下的遍历过程中，如果碰到一个节点是有两个儿子的，意味着这里要做一次合并操作。返回值里需要加上(1<<dep)，因为两个子树在deo深度值不一样，这一位就是有贡献的。

ll dfs(int now,int dep)//当前在哪个节点，遍历到的深度 
{
	if(dep<0) return 0;
	int ls=tr[now][0];int rs=tr[now][1];
	if(R[ls]&&R[rs])//有两个儿子，此处出现分叉，需要合并 
	{//考虑遍历左子树，对于每一个值更新两颗子树合并的最小代价 
		int num=1e9;
		for(int i=L[ls];i<=R[ls];++i)
		{
			num=min(num,query(rs,mas[i],dep-1));//深度-1，因为在当前深度下两个子树还是共用一个节点 
		}
		return dfs(rs,dep-1)+dfs(ls,dep-1)+num+(1<<dep);
	}
	if(R[ls]) return dfs(ls,dep-1);
	if(R[rs]) return dfs(rs,dep-1);
	return 0;
}

然后查找子树合并的最小代价，其实就是一个板子了

int query(int now,int val,int dep)
{
	if(dep<0) return 0;
	int id=(val>>dep)&1;
	if(tr[now][id]) return query(tr[now][id],val,dep-1);
	else return query(tr[now][id^1],val,dep-1)+(1<<dep);
}

代码也是很好写

code：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define IL inline
const int N=2e5+10;
int tr[N*40][3];
int n;
int mas[N];
int L[N*40],R[N*40];
int cnt=0;
namespace FastIOT{
	const int bsz=1<<18;
	char bf[bsz],*hed,*tail;
	inline char gc(){if(hed==tail)tail=(hed=bf)+fread(bf,1,bsz,stdin);if(hed==tail)return 0;return *hed++;}
	template<typename T>IL void read(T &x){T f=1;x=0;char c=gc();for(;c>'9'||c<'0';c=gc())if(c=='-')f=-1;
	for(;c<='9'&&c>='0';c=gc())x=(x<<3)+(x<<1)+(c^48);x*=f;}
	template<typename T>IL void print(T x){if(x<0)putchar(45),x=-x;if(x>9)print(x/10);putchar(x%10+48);}
	template<typename T>IL void println(T x){print(x);putchar('\n');}
}
using namespace FastIOT;
void insert(int id)
{
    int p=0;
	for(int i=30;i>=0;--i)
	{
	     int ik=(mas[id]>>i)&1;
	     //cout<<mas[id]<<' '<<i<<' '<<p<<' '<<" "<<ik<<' '<<tr[p][ik]<<endl;
		 if(!tr[p][ik])
		 {
		 	tr[p][ik]=++cnt;
		 	L[cnt]=1e9;//极小值 
		 }
		 p=tr[p][ik];
		 L[p]=min(L[p],id);
		 R[p]=max(R[p],id);
	}	
}
int query(int now,int val,int dep)
{
	if(dep<0) return 0;
	int id=(val>>dep)&1;
	if(tr[now][id]) return query(tr[now][id],val,dep-1);
	else return query(tr[now][id^1],val,dep-1)+(1<<dep);
}
ll dfs(int now,int dep)//当前在哪个节点，遍历到的深度 
{
	if(dep<0) return 0;
	int ls=tr[now][0];int rs=tr[now][1];
	if(R[ls]&&R[rs])//有两个儿子，此处出现分叉，需要合并 
	{//考虑遍历左子树，对于每一个值更新两颗子树合并的最小代价 
		int num=1e9;
		for(int i=L[ls];i<=R[ls];++i)
		{
			num=min(num,query(rs,mas[i],dep-1));//深度-1，因为在当前深度下两个子树还是共用一个节点 
		}
		return dfs(rs,dep-1)+dfs(ls,dep-1)+num+(1<<dep);
	}
	if(R[ls]) return dfs(ls,dep-1);
	if(R[rs]) return dfs(rs,dep-1);
	return 0;
}
void solve()
{
	read(n);
	for(int i=1;i<=n;++i) read(mas[i]);
	sort(mas+1,mas+1+n);
	for(int i=1;i<=n;++i)
	{
		insert(i);
	}
//	L[0]=1;R[0]=n;
//	cout<<R[tr[0][0]]<<' '<<R[tr[0][1]]<<endl;
//	cout<<tr[0][0]<<' '<<tr[0][1]<<endl;
	cout<<dfs(0,30);
}
int main()
{
	//ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	solve();
	return 0;
}