导读
自OpenAI 2022年底发布ChatGPT以来,大语言模型便一直是最火热的话题。虽然大语言模型展示出了强大的能力,但是其大规模参数量也对计算和存储资源提出了较高的要求。一些研究人员便开始研究对大语言模型参数压缩的方法,其中最广泛应用的就是常规标量量化方法了,例如4-bit量化。然而,由于常规标量量化方法数值表达范围的限制,这使得LLM参数低比特量化难以取得较好的结果。有一些研究人员另辟蹊径,通过在codec模型中常用的VQ(Vector Quantization)的方法,并取得了不错的结果,这标志着突破LLM常规标量量化瓶颈的重要进展,本文将介绍几个对LLM权重进行VQ处理方法。
©️【深蓝AI】编译
01 背景知识
Vector Quantization
Vector Quantization,属于一种数据压缩技术,具体而言,这是一种把高维向量映射至一组预先设定好的低维向量之上,并且低维向量事先被存储于码本(codebook)当中的技术。

具体地来看,通常的VQ操作分为以下几个步骤,

对原始的向量进行K-means操作,把这些向量分成若干个簇(这些簇共同构成了codebook),每个簇有一个中心(图中的c1-c5)

对向量进行量化的过程就是寻找向量所归属的簇,或者寻找距离向量最近的中心,接着用中心的index来替代原始的向量,得到量化之后的结果。

从理论上来讲,VQ就是在数据中寻找共性以及去除数据中的冗余,因此,它可以实现比标量量化更高的数据压缩效率,这也就是把VQ用于LLM权重压缩的理论基础。
Residual Vector Quantization
虽然上文所述的Vector Quantization取得了比较好的压缩效果,但是这样的量化过程会损失掉不少信息。
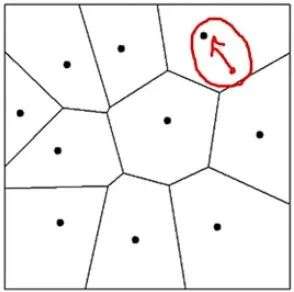
例如上图中红点部分代表的向量,经过量化之后就会丢失掉红色箭头代表的向量中隐含的信息,为了避免丢失掉这种寻找最近中心带来的信息损失,研究人员继续对红色向量进行第二次量化,这就是残差向量量化,Residual Vector Quantization。
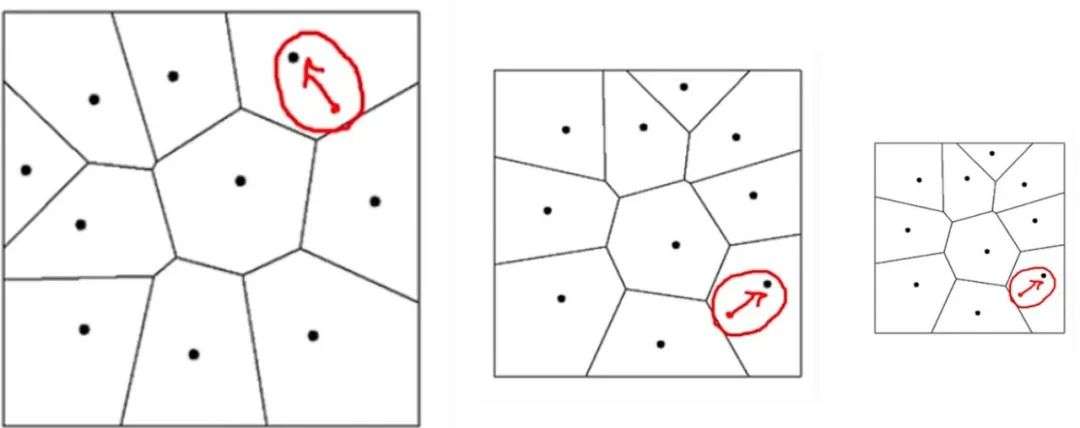
以此类推,可以迭代式的逐步对残差进行量化,最终得到较高精度的量化结果。

上图便演示了进行三次量化操作的过程,绿色向量经过量化得到index 3,残差的红色向量进行第二次量化得到index 12,残差的蓝色向量进行第三次量化得到index 91,因此该绿色向量经过量化之后得到[3,12,91],这个index组合。综上所述,Residual Vector Quantization这种方法可以通过多次量化并对结果进行加和的方式得到一个更好的重建还原的效果。
参数量化方法
均匀量化(Uniform quantization)一个对称均匀量化器( symmetric uniform quantizer)将原始的浮点向量 x ∈ R^D 近似为 x ≈ sxint,其中 xint 中的每个元素都是一个 b 位的整数值,s 是一个更高精度的量化调节参数,适用于x的每一个维度。
非均匀量化(Non-Uniform quantization)如上文所述,均匀量化虽然高效,但它非常不灵活,因为只能表示等距分布的点。一种更灵活的量化方法是使用基于码本量化( codebook quantization)的非均匀量化,其中浮点数被离散化为码本 C 中的任意标量质心( scalar centroids):C = {c1, c2,..., ck}。然后,x 中的每个高精度值都由质心 cj 的索引 j 表示。每个索引可以使用⌈log2 k⌉位进行存储。
向量量化(Vector quantization)在上一段介绍的非均匀量化的方法中,我们假设 x 中的每个维度值都是单独进行量化的。然而,其实还可以构建一个更灵活的量化器,为整个向量进行编码,得到一个更加高维的质心码表C。在这种情况下,C 中的每个质心编码 d 个值,例如,如果 d = 2,则为值对,并且 x 中的每个 d 个值都由一个指向 Cd 的索引表示,这里我们使用 Cd 表示具有维度为 d 的元素的码本。这种技术被称为向量量化(VQ)。将 D 维向量拆分为多个 d 维子向量(d < D),每个子向量都由指向 Cd 的一个索引单独表示的情况,也经常被称为乘积量化。
02 VQ量化LLM weights方法
VQ量化LLM权重面临的挑战
虽然VQ可以突破标量量化的瓶颈,但是将VQ方法应用于LLM权重压缩还面临着以下挑战:
1.在极低比特压缩率的情况下保证压缩的精度;
2.由于LLM参数庞大,在LLM上如何高效的应用压缩量化算法; 3.从量化压缩的权重之中还原原有的模型权重带来的计算开销; 因此,后文将介绍几篇用VQ对LLM进行权重压缩的工作,以及研究人员应对上述几个挑战的思路。
AQLM
AQLM,全称为Extreme Compression of Large Language Models via Additive Quantization(论文链接:https://arxiv.org/pdf/2401.06118)。
研究人员在这篇论文里面自称是第一篇将RVQ方法应用到对LLM权重压缩中的工作。虽然论文中所述采用的VQ方式是Additive Quantization(AQ),但是其实AQ和RVQ没有本质区别,都是对嵌入向量进行多级编码之后再进行加和。
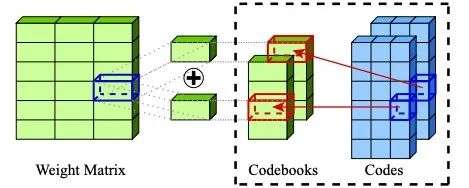
例如,对于一个权重为![]() 的线性层,找到一组量化还原后的权重
的线性层,找到一组量化还原后的权重![]() ,使得一组相同的input data
,使得一组相同的input data ![]() ,
,![]()
![]() 和
和![]()
![]() 之间的MSE最小化。
之间的MSE最小化。
其中,![]() 是经过AQ重建还原得到的权重矩阵,假设AQ有M个codebook
是经过AQ重建还原得到的权重矩阵,假设AQ有M个codebook ![]() ,则重建还原的权重矩阵
,则重建还原的权重矩阵![]() 通过如下方式得到
通过如下方式得到

即通过对每一级codebook中的code加和汇总得到。 因此,训练这样一个AQ模型的优化目标就变成了如下式子

因此,通过最小化上述MSE误差来更新AQ模型的codes,而具体训练这个模型的步骤如下:
-
K-means初始化:就像标准的RVQ一样,先对weight的 K-means 聚类并保存生成的索引,然后通过从每个权重中减去最近的centroid来计算量化误差,重复对量化误差进行 K-means 聚类,迭代上述过程若干次,得到多级codebook。
-
Beam search求解code:为了得到最小的MSE code index组合,研究人员采用了beam search的方法寻找k组mse最小的code index组合。这个过程其实也和LLM推理解码的过程类似,因此把beam search应用于求解code组合不失为一种简单且高效的方法。
-
更新codebook:在上述步骤通过beam search 找到最优的code book组合之后,为了使得上述目标函数能够更好的适用于adam优化器,研究人员对目标函数做了如下修改。

-
层间微调:由于AQLM是对每层的权重单独进行量化压缩的,而每层权重的压缩还原误差不尽相同,为了避免这样的误差问题,研究人员在对transformer block层中除线性层外的其他部分进行了微调,以部分弥补压缩还原带来的误差累积问题。
-
还原参数:AQ对模型权重压缩之后会得到一组索引,再根据索引找到codebook中的codes,一起组成压缩得到的编码vector。

看到这里难免会有疑问,VQ仅仅是对Transformer Blocks中的线性层进行参数压缩,而其他部分仍然需要微调以弥补部分量化带来的损失的话,这样的压缩操作意义是什么?研究人员也在论文中给出了解答:尽管对Transformer Blocks的其他部分微调需要消耗一定的计算资源,但是由于整体上需要微调的参数较小(基本也就是QKV矩阵),因此用于优化器状态的 VRAM 很少。而且这个微调过程不需要很多训练步骤,通常迭代几步就可以完成,这是由于本身参数从一个良好的初始状态进行初始化,以及量化带来的误差不会过大。论文中表示,通常微调过程只占总压缩时间的10%-30%不到。

研究人员选取了Llama 7B 13B 70B三种参数规模的模型进行压缩重建还原实验,实验结果显示在2 bit per parameter的压缩比例下(fp32 是32 bit per parameter)取得了良好的效果,证明了VQ压缩路线的可行性。
GPTVQ
顾名思义,这篇工作就是应用于GPT的VQ方法。研究人员通过对Llamav2 70B应用这种方法,甚至可以应用在手机CPU上面,论文全称为GPTVQ: The Blessing of Dimensionality for LLM Quantization,论文链接:https://arxiv.org/pdf/2402.15319。
虽然低比特量化(如4bit)已经取得了较好的成果,但是这都是对LLM进行均匀量化(uniform quantization)的方法。这篇工作探索了非均匀量化(即VQ方法)对LLM压缩的潜力。

如上图所示,VQ方法可以比均匀量化,非均匀量化更好的表示2d标准正态分布,这也是为什么对LLM权重采用VQ方法进行压缩可以突破当前均匀量化瓶颈的理论基础。
而且与上文AQLM方法不同的是,AQLM仍然需要对Transformer Block其他部分进行微调以弥补量化带来的损失,但GPTVQ的研究人员认为,这样的微调对于目前的LLM来讲,仍然需要消耗大量的计算资源。因此,他们探索了一种快速且可扩展的量化方法,通过在量化时把激活值也考虑进来,这样便可以高效地把量化方法扩展应用到参数量非常大的模型了,而不用再通过微调处理弥补量化损失。

对权重进行VQ的具体方法如下,假设我们需要一次性对一个维度为d的向量进行量化,那么在标量量化的情况下,对每个维度进行四舍五入就是最优的量化方法。但是,如果是应用VQ方法,简单地选择最近的质心可能不是最优的,因为在 d 个坐标中的每个坐标的误差权重是不同的。 因此研究人员制定了如下规则用以选择最优的质心:
![]()
同时,为了进一步降低量化压缩的误差,与AQLM对整个weight matrix做vq操作不一样的是,这篇工作将weight matrix分成了不同的group,每次仅对一个group中的weight进行vq操作,接着根据这一个group的重建loss作为残差更新下一个group。 此外,研究人员还对codebook初始化的方法进行了调整,给定 d 维向量 x(i) 的集合,目标是找到 k 个质心向量 c(m) 以及相应的分配集合 Im,使得如下的海森加权距离函数的总和最小:

为了进一步降低向量量化带来的误差,研究人员还在codebook初始化之前应用了block间数据初始化,对于每个需要进行量化的权重参数组,研究人员对权重子矩阵 Wi 执行按相应的尺度 Si 进行元素级量化缩放 Wi ⊘ Si,其中缩放系数按照如下方式确定:
![]()
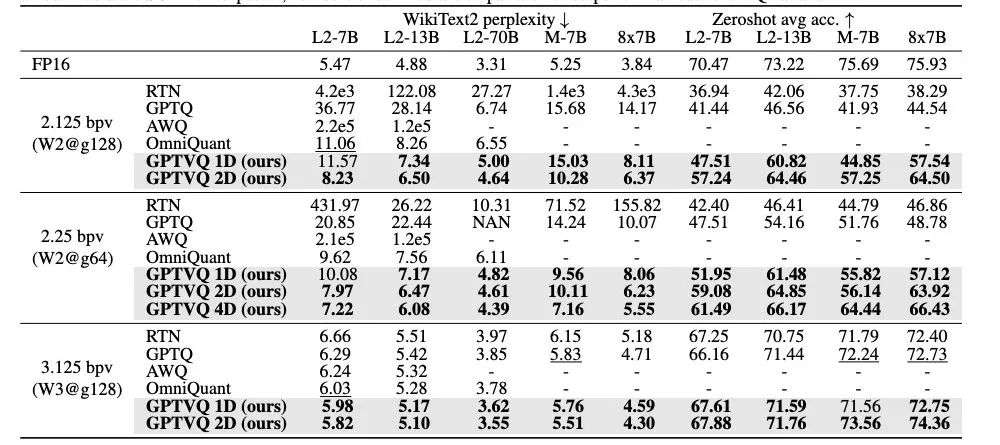
通过ppl和平均准确率作为比较指标,GPTVQ方法在几个主流的LLM(Llama2,Mistral,Mistral MoE)上进行压缩还原均取得了良好的结果。
VPTQ
在GPTVQ的基础之上,VPTQ做了更细粒度的量化操作。研究人员认为GPTVQ是q列一起VQ的,这样可能会带来比较大的损失累积,所以VPTQ是对weight中的每列进行独立的VQ操作,在一列上拆成m个vector然后再进行VQ操作。对于更大的weigth matrix,还会把weigt 拆成多个group,每个group拥有自己的codebook。论文全称为VPTQ: Extreme Low-bit Vector Post-Training Quantization for Large Language Models,论文链接https://arxiv.org/pdf/2409.17066。

由上文可得,研究人员通常把VQ对LLM权重压缩建模成如下优化目标:

而在VPTQ中,研究人员进一步地把上式建模成了一个二阶优化方案,采用拉格朗日方法把这个优化问题转化成了不带约束的优化问题:
![]()
那么,它的对偶问题可以通过下式表达:
![]()
对λ求导之后就可以得到
![]()
那么最优的λ则有

在codebook初始化方法上面,VPTQ也做了相应的调整以适应优化目标,通过利用矩阵迹的循环特性以及哈达玛积来转换优化目标。

因此把优化目标分成了两项,第一项表示初始误差矩阵的主要对角元素,这对量化误差有显著影响。第二项是权重量化中的单个值与其他值的相互作用。且由于因为海森矩阵主要是对角矩阵,可以通过codebook初始化优先优化第一项,因此可以把第一项看成是一个带权重的K-means聚合方法(Weighted K-means Clustering)。
综上所述,在有效带宽量,准确率和低比特量化平衡,量化编码耗时以及推理吞吐量上均取得了优势,超过了前文所提到的AQLM和GPTVQ方法。
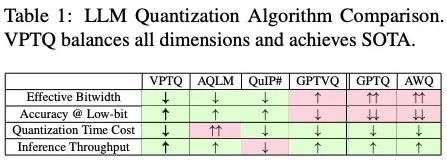
毫无疑问,最SOTA的方案当然是VPTQ。

03 总结
从上文梳理的研究内容不难发现,VQ方法确实可以突破常数量化的瓶颈,取得更高的压缩比例,且将VQ方法应用于LLM参数压缩在随着研究的深入渐渐变得成熟。
从AQLM首次把VQ应用到LLM上,经过GPTVQ和VPTQ的迭代已经逐渐形成了一定的范式,未来有望进一步地降低LLM的使用门槛,使得LLM可以在更加普适的场景下得以应用,发挥更大价值。
04 参考文献
1.Oord, Aäron van den et al. “Neural Discrete Representation Learning.” Neural Information Processing Systems (2017).
2.Egiazarian, Vage et al. “Extreme Compression of Large Language Models via Additive Quantization.” ArXiv abs/2401.06118 (2024).
3.Baalen, Mart van et al. “GPTVQ: The Blessing of Dimensionality for LLM Quantization.” ArXiv abs/2402.15319 (2024).
4.Liu, Yifei et al. “VPTQ: Extreme Low-bit Vector Post-Training Quantization for Large Language Models.” ArXiv abs/2409.17066 (2024).





















 472
472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








