leetcode hot100 之 柱状图中最大的矩形

题目

给定一个数组，表示一系列连续的柱子，每个数字代表柱子的高度，宽度统一为 1。求在这个柱状图当中最大能构建的矩形面积。

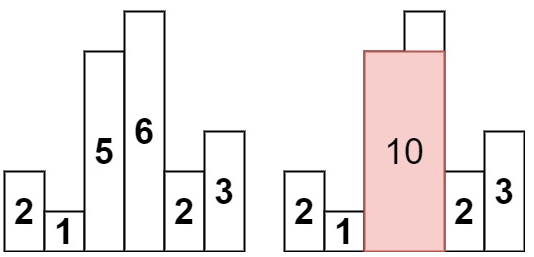
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

原题链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

思路

思路1

动态规划。记 dp[i][j] 表示 i 到 j 之间，最小的高度。可以初始化 dp[i][i] = heights[i]，且已知 j >= i。那么转移方程为 dp[i][j] = min(dp[i][j - 1], heights[j])。
那么端点在 i、j 上的最大矩阵面积为 dp[i][j] * ( j - i + 1)，在求 dp 的过程中，不断更新全局最大矩阵面积即可。
但这种方式时间复杂度为 O(n^2)，leetcode 上没法通过，有没有更好的方法呢？答案肯定是有的，那就是采用单调栈了。

思路2

单调栈。顾名思义，就是栈中的元素保持递增或递减的顺序。
我们先来重新看题。换一个思路，如果我们遍历数组，计算n个矩阵，以位置 i 上的柱子（暂且称为h）的高度作为高，则其宽就等于，当前位置向左向右所能够够到的最左端柱子和最右端柱子，其边界应该是第一个高度小于 h 的柱子。所以问题转变成了，找到位置 i ，其最左端边界柱子的下标，和最右端的下标。
我们采用单调栈来记录柱子的下标，并保证单调栈中的柱子高度是单调递增的。
当遍历到位置 i 时，如果 heights[i] > heights[top]，则说明 top 是 i 的左边界；如果 heights[i] <= heights[top] 则说明 top 不是 i 的左边界，为了找到这个左边界，需要不断的从栈中弹出，直到找到该边界为止。然后将 i 入栈，成为新的 top。
因为 i 的高度 heights[i] 比刚才弹出来的位置的高度都要小，所以后面 i+1、i+2 等等的左边界至多只会是 i （相当于 i 进行了截断），所以不需要再管那些弹出的数据。
另外需要考虑特殊情况，如果栈为空，则记左边界为 -1，即数组的最左端为左边界。

按照上面的思路，我们从前往后遍历找到了左边界，那右边界可以按相同的方法从后往前遍历来求解。

不过，这里还可以进一步优化，将遍历两次优化成遍历一次。

我们先初始化所有位置的右边界为 n。回顾刚才我们在需要弹出操作时的判断条件是，height[i] <= heights[top]。如果 height[i] < heights[top]，实际也说明了 top 最近的右边界是 i，但是如果 height[i] == heights[top] 呢？此时 top 的右边界不一定是 i，但是，实际上 top 和 i 位置的柱子，是等价的。我们只需要保证有一个柱子的左右边界是准确的，就不会影响最终的 max_area 的求解。所以我们暂且虚拟地认为 top 的最近右边界为 i。那么在弹出操作过程中，也就可以找到右边界了。

最后再根据公式 (right - left - 1) * height 求解矩阵面积。

• 复杂度分析
  • 时间复杂度 O(n)。遍历一次求左右边界，再遍历一次求最大矩形。
  • 空间复杂度 O(n)。用两个长度为 n 的数组存左右边界。

代码

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int max_area = -1;
        int n = heights.size();
        vector<int> left(n, -1);
        vector<int> right(n, n);
        stack<int> mono_stack;
        for (int i = 0; i < n; i++) {
            while(!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {
                right[mono_stack.top()] = i;
                mono_stack.pop();
            }
            if (!mono_stack.empty()) {
                left[i] = mono_stack.top();
            }
            mono_stack.push(i);
        }
        for (int i = 0; i < n; i++) {
            int cur_area = (right[i] - left[i] - 1) * heights[i];
            max_area = max(max_area, cur_area);
        }
        return max_area;
    }
};