LeetCode hot 100—柱状图中最大的矩形

题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例

示例 1:

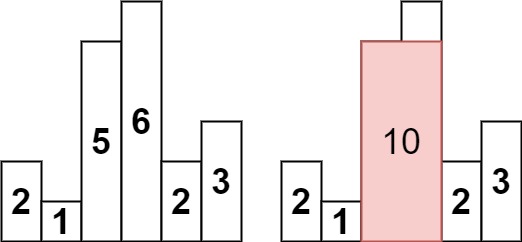
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

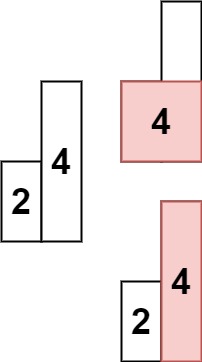
输入： heights = [2,4]
输出： 4

分析

为了求解柱状图中能够勾勒出的最大矩形面积，我们可以使用单调栈算法来优化计算过程。该算法通过维护一个单调递增的栈来快速找到每个高度左右两侧第一个比它小的高度，从而确定以当前高度为高的最大矩形宽度。

单调栈法

方法思路

单调栈：维护一个存储下标（对应柱状图高度）的栈，栈中的下标对应的高度保持单调递增。

边界处理：在柱状图高度数组末尾添加一个高度为 0 的虚拟元素，确保最后一个元素也能被处理。

遍历计算：对于每个高度，若当前高度小于栈顶高度，则弹出栈顶元素并计算以该高度为高的矩形面积。通过栈中剩余元素确定左右边界，计算宽度并更新最大面积。

时间复杂度：O()，  是数组的长度

空间复杂度：O()

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> h = heights;
        h.push_back(0); // 添加虚拟元素，确保处理最后一个元素
        stack<int> st; // 存储下标，对应的高度单调递增
        st.push(-1); // 初始边界下标，避免栈空
        int maxArea = 0;
        
        for (int i = 0; i < h.size(); ++i) {
            while (st.top() != -1 && h[i] < h[st.top()]) {
                int top = st.top();
                st.pop();
                int width = i - st.top() - 1; // 左右边界之间的宽度
                maxArea = max(maxArea, h[top] * width);
            }
            st.push(i);
        }
        return maxArea;
    }
};

该方法通过单调栈高效地找到每个高度的左右边界，避免了暴力解法中的重复计算，是求解此类问题的最优解法之一。