bzoj 2120 数颜色（分块做法）

最新推荐文章于 2020-09-11 21:07:44 发布

原创最新推荐文章于 2020-09-11 21:07:44 发布 · 476 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#acm

个人知识管理专栏收录该内容

20 篇文章

订阅专栏

本文介绍了解决BZOJ2120数颜色问题中的修改操作方法，使用分块策略及ppp数组追踪颜色变化，实现高效查找与更新。文章详细解释了如何利用ppp数组和pre数组来快速定位颜色变动前后的位置。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

bzoj 2120 数颜色（分块做法）

此篇文章主要讲修改操作
用pre[i]表示第i个元素的前一个相同元素的位置，问题变成在区间[l,r]里找大于l的数的个数,
（具体什么意思去其他地方看）默认值为最大值。
用ppp[i]表示颜色i最后出现的位置（针对这道题颜色最多1e6种，建一个1e6的数组即可）
color[i]表示第i个位置是什么颜色
总个数为n

1.建区块（网上有）

2.查询操作（网上有）

3.修改操作

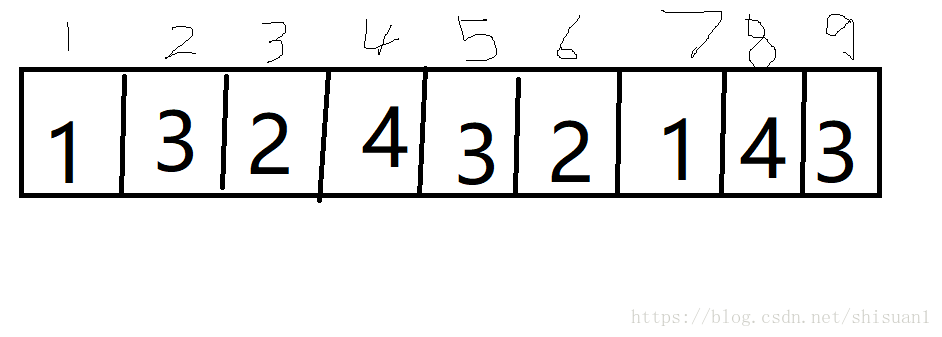
建好的color数组
这个是color数组
修改操作的主要问题是如何在序列后找到修改之前的颜色的第一个位置
和
修改之后的颜色前一个位置，后一个位置
这里就要用到ppp数组解决这个问题
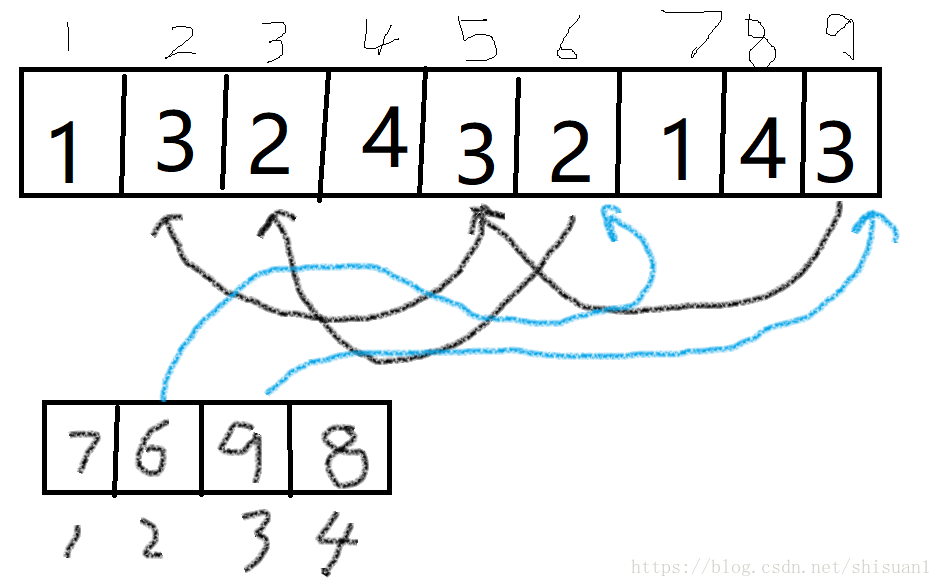
这里写图片描述
上图下面的那个数组是ppp数组
比如将5号位置的3修改为2

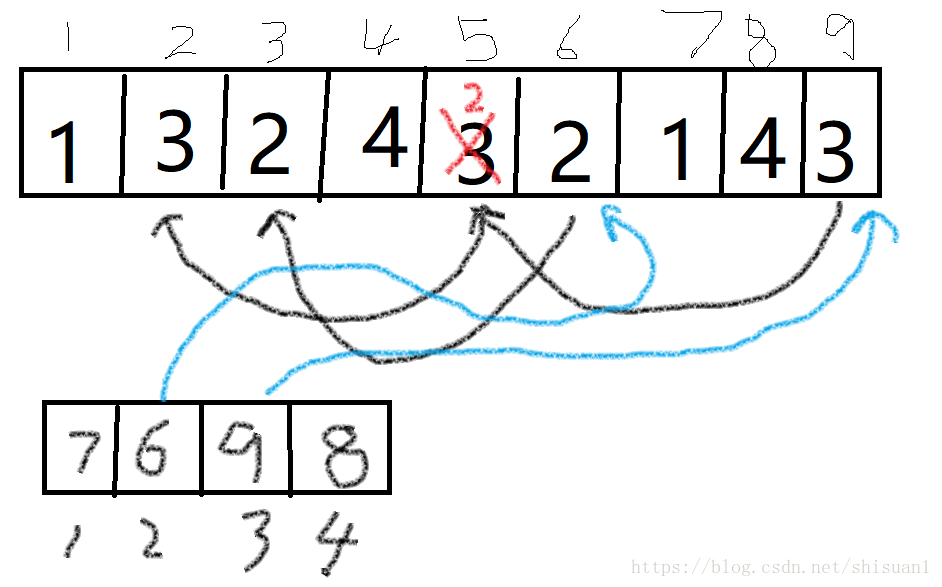
那么我们要更改值的位置则为五号位置后面的3和2
问题就是如何寻找颜色2，3
很简单，如图这是一个链式结构，只要我们从ppp数组中找到相应元素的最后位置，在通过pre数组的值往前找就可以了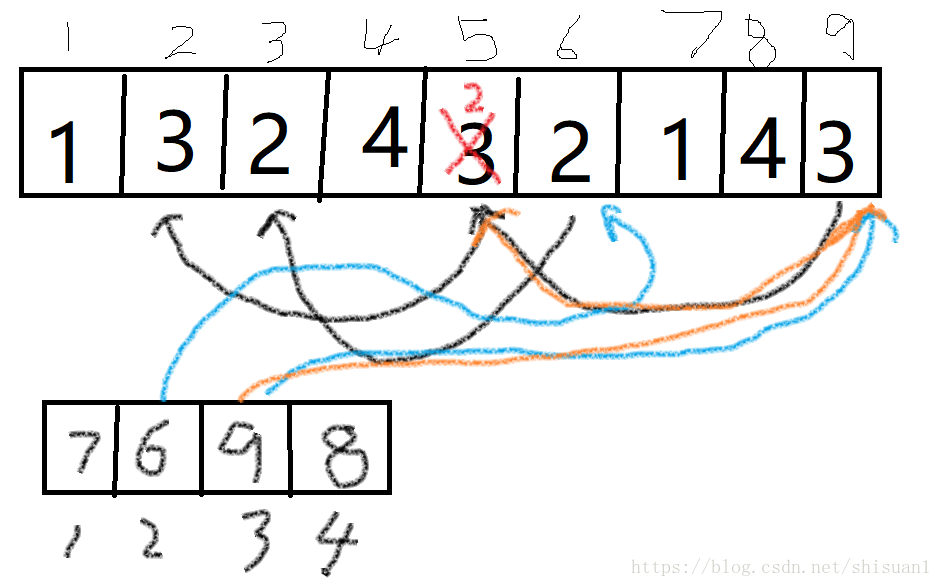这里写图片描述
沿棕色的线寻找3

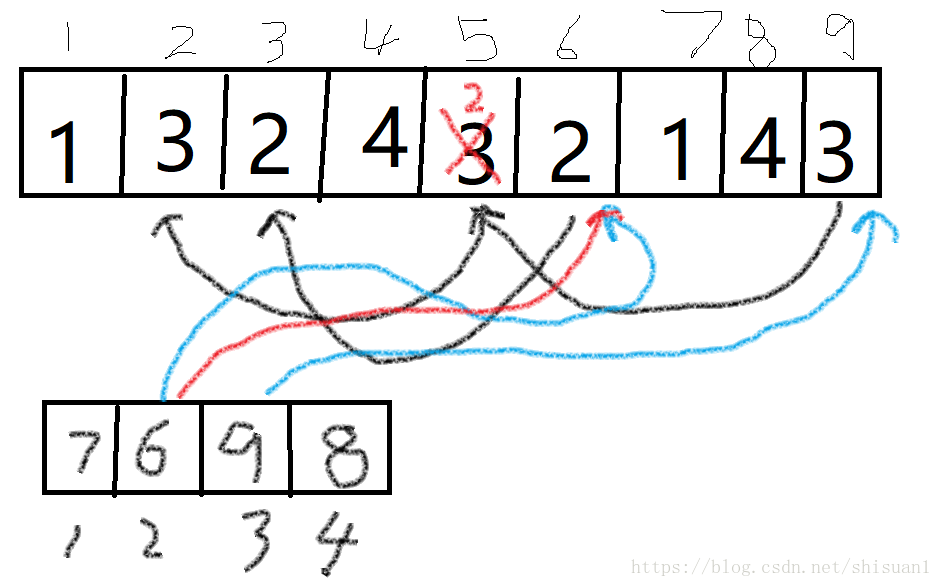
沿红色的线寻找2
找到位置改值再对相应的块进行重构修改就完成了。注意维护ppp数组的值始终保持为最后一个元素值

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#define inf 0x3f3f3f3f
using namespace std;
int a[205][205];
int pre[200005];
int color[200005];
int ppp[1000005];
int n,m,l,r;
void reset(int x)
{
    int p=(x-1)/l;
    for(int j=1;j<=l;j++)
    {
            a[p][j]=pre[p*l+j];
    } 
    sort(a[p]+1,a[p]+l+1);
}
void build()
{
    for(int i=0;i<r;i++)
    {
        for(int j=1;j<=l;j++)
        {
            a[i][j]=pre[i*l+j];
        } 
        sort(a[i]+1,a[i]+l+1);
    }
}
int search(int x,int y)
{
    int ans=0;
    int p=(x-1)/l+1;
    int q=(y-1)/l;
    if(p>=q)
    {
    for(int i=x;i<=y;i++)
    if(pre[i]<x)
    ans++;
    return ans;
    }
    for(int i=x;i<=p*l;i++)
    if(pre[i]<x)
    ans++;
    for(int i=q*l+1;i<=y;i++)
    if(pre[i]<x)
    ans++;
    for(int i=p;i<q;i++)
    {
        ans+=lower_bound(a[i]+1,a[i]+l+1,x)-a[i]-1;
    }
    return ans;
}
void change(int x,int y)//位置x,颜色y.
{
    int p=color[x];
    color[x]=y;
    int c=ppp[p];
    if(c==x)
    {
    ppp[p]=pre[c];  
    }
    else
    {
        while(pre[c]!=x)
        c=pre[c];
        pre[c]=pre[x];
        reset(c);   
    }
    c=ppp[y];
    if(c<x)
    {
        pre[x]=c;
        ppp[y]=x;
        reset(x);
    }
    else if(pre[c]<x)
    {
        pre[x]=pre[c];
        pre[c]=x;
        reset(x);
        reset(c);
    }
    else
    {
        while(pre[c]>x)
        {
        c=pre[c];
        }
        pre[x]=pre[c];
        pre[c]=x;
        reset(x);
        reset(c);
    }
} 

int main()
{
    //freopen("input.txt","r",stdin);
    memset(ppp,0,sizeof(ppp));
    memset(pre,inf,sizeof(pre));
    pre[0]=0;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&color[i]);
        if(ppp[color[i]]!=0)
        pre[i]=ppp[color[i]];
        else
        pre[i]=0;
        ppp[color[i]]=i;
    }
    l=floor(sqrt(n));
    if(n%l>0)
    r=n/l+1;
    else
    r=n/l;
    build();
    /*printf("%d %dff\n",l,r);
    for(int i=1;i<=n;i++)
    printf("%d ",pre[i]);
    puts("");*/
    int x,y;
    char c[10];
    for(int i=0;i<m;i++)
    {
        scanf("%s%d%d",c,&x,&y);
        if(c[0]=='Q')
        printf("%d\n",search(x,y));
        else
        change(x,y);
    }
    return 0;
}