浅谈控制原理以及PID

       最近一个月，围绕公司业务，学习了一下控制原理以及pid的设计与参数整定，学的不算深，在这里结合matlab对目前所学进行一些整合，本篇所描述内容包含自己的理解，可能需要一定的系统知识基础。

为什么需要使用控制器

       首先来做个实验，如果不使用任何控制器，系统能否进行自身调节呢？以下面这个二阶开环系统为例，输入是阶跃信号，表示参考值，查看其仿真输出。

       可以发现，即使不添加控制部分，系统自身也能被输入拉到指定参考值（想想为什么？），只是达到稳态的时间很久。这是因为上述系统具有两个负实部的极点，由信号系统的相关知识可知，该系统具有稳定性，即：有限的输入产生有限的输出。另外，观察零极点图：

       该系统的两个极点中，将远离虚轴（左边）的极点称为极点1，靠近虚轴（右边）的极点称为极点2，如果将s域的传递函数转化为时域的冲激响应如下图所示：

注：该图实际仅画出极点的趋势，并非响应的准确描述，但趋势是确定的

       发现靠近虚轴的极点（极点2）在响应中占据主导低位，收敛的趋势缓慢，从而使响应和的收敛速度变慢，进而验证了前面系统稳态时间长的实验结果，而极点1虽然自身产生的响应收敛速度快，但在线性系统里被极点2产生的响应给“拖累”了。这里的响应，本质就是不同极点对应着不同指数的自然对数的和，即：

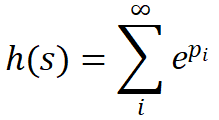
       当极点p从左半轴越靠近虚轴，的衰减越慢，相反，远离虚轴，其衰减越快。而由欧拉公式可知，如果极点具有虚部，会产生不同程度的正弦震荡。

       同样，该响应曲线最终趋于0，也验证了系统的稳定性。

       在这里还有一个问题，为什么输入一个参考值1，得到的响应最终就是趋于1呢？如果输入参考值为10，响应最终也是10吗？这就需要用到拉普拉斯的终值定理了，我们知道，阶跃信号在s域的变换为，由终值定理可知：

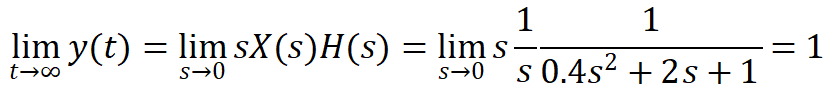
       如果输入参考值为10，则输入信号的s域变换变为，即只改变了增益，由上述式子可知，响应最终也会趋于10。但要注意，拉普拉斯终值定理的使用是有条件的!

       以上的分析都针对一个开环系统，如果一个系统的传递函数已知，则针对系统特性直接使用开环控制也是可以的，但实际应用中往往系统比较复杂，且受到环境、人为等多方面因素的影响，很难采用简单的方式进行开环控制，因此需要不断的根据实时输出动态地调整输入，即