opengl下的视锥体剔除和凸多边形剔除

预备知识

法线方程表达式的一般形式为Ax+By+Cz+D=0，其中(A,B,C)是平面的法向量，D是平面的截距。

平面上一点为P(x0,y0,z0)，则点P到平面的距离为：d = |Ax0+By0+Cz0+D| / √(A²+B²+C²) (因为法向量没有归一化，所以得到法向量上的投影要除以法向量长度)

假设n是归一化后的法向量(A,B,C)，平面上存在任意一点P(x,y,z)，O为原点，那么

OP·n = |OP|·|n|·cos(delta) = Ax+By+Cz 

因为P要满足平面方程，所以 Ax+By+Cz = -D

OP·n的几何意义是OP在n上的投影，即为平面距离原点的距离，故平面距离原点的距离为-D

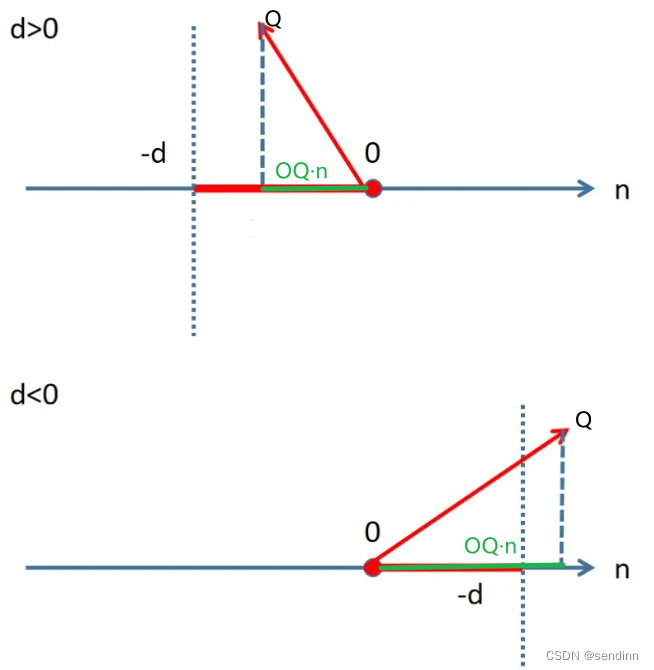
当D是正数，那么平面一定是从原点开始，沿着n向其反方向移动了|d|的长度。

当D是负数，那么平面一定是从原点开始，沿着n向其正方向移动了|d|的长度。

平面外任意一点Q(x,y,z)点乘n是OQ在n上投影的距离(可正可负)，加上D的值就是点到平面的距离。

点在正面

点在反面