Day
1
2022.01.22
\texttt{Day 1 2022.01.22}
Day 1 2022.01.22 开幕式,好耶!

Day 2 2022.01.23 \texttt{Day 2 2022.01.23} Day 2 2022.01.23
上午
才知道课程都是二选一,选了个第二课堂听听。
前置
- 向量加减
{ p = ( x 1 , y 1 ) , q = ( x 2 , y 2 ) p + q = ( x 1 + x 2 , y 1 + y 2 ) p − q = ( x 1 − x 2 , y 1 − y 2 ) \begin{cases} p = (x_1,y_1),q = (x_2,y_2)\\ p + q = (x_1 + x_2,y_1 + y_2)\\ p - q = (x_1 - x_2,y_1 - y_2) \end{cases} ⎩ ⎨ ⎧p=(x1,y1),q=(x2,y2)p+q=(x1+x2,y1+y2)p−q=(x1−x2,y1−y2)
- 向量点积【标量】
{ A B → ⋅ C D → = x 1 x 2 + y 1 y 2 A B → ⋅ C D → = ∣ A B ∣ ∣ C D ∣ cos θ \begin{cases} \overrightarrow{AB} \cdot \overrightarrow{CD} = x_1x_2 + y_1y_2\\ \overrightarrow{AB} \cdot \overrightarrow{CD} = |AB||CD| \cos \theta \end{cases} {AB⋅CD=x1x2+y1y2AB⋅CD=∣AB∣∣CD∣cosθ
- 向量叉积【矢量】
{ A B → × C D → = x 1 y 2 − x 2 y 1 A B → × C D → = ∣ A B ∣ ∣ C D ∣ sin θ \begin{cases} \overrightarrow{AB} \times \overrightarrow{CD} = x_1y_2 - x_2y_1\\ \overrightarrow{AB} \times \overrightarrow{CD} = |AB||CD|\sin \theta \end{cases} {AB×CD=x1y2−x2y1AB×CD=∣AB∣∣CD∣sinθ
同时有 0 × a = a × 0 = a × a = 0 \bold{0} \times \bold{a} = \bold{a} \times \bold{0} = \bold{a} \times \bold{a} = \bold{0} 0×a=a×0=a×a=0。
∣ a × b ∣ |\bold{a} \times \bold{b}| ∣a×b∣ 在数值上等于 a , b \bold{a},\bold{b} a,b 构成的平行四边形的面积。
- 向量旋转
a = ( x , y ) \bold{a} = (x,y) a=(x,y),逆时针旋转 θ \theta θ 后为 a ′ = ( x cos θ − y sin θ , x sin θ + y cos θ ) \bold{a'} = (x \cos \theta - y \sin \theta,x \sin \theta + y\cos \theta) a′=(xcosθ−ysinθ,xsinθ+ycosθ)。
- 多边形面积
S = 1 2 ∣ ∑ i = 1 n V i × V i m o d n + 1 ∣ S = \frac{1}{2}|\sum_{i = 1}^{n} V_i \times V_i \mod n + 1| S=21∣∑i=1nVi×Vimodn+1∣
-
极坐标与极坐标系
-
误差判断
double eps = 1e-8;
return (x > eps) - (x < eps);
距离
- 欧式距离
二维 ∣ A B ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 |AB| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} ∣AB∣=(x2−x1)2+(y2−y1)2
三维 ∣ A B ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 |AB| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} ∣AB∣=(x2−x1)2+(y2−y1)2+(z2−z1)2
- 曼哈顿距离
d ( A , B ) = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ d(A,B) = |x_1 - x_2| + |y_1 - y_2| d(A,B)=∣x1−x2∣+∣y1−y2∣
- 切比雪夫距离
d ( A , B ) = max ( ∣ x 1 − x 2 ∣ , ∣ y 1 − y 2 ∣ ) d(A,B) = \max (|x_1 - x_2|,|y_1 - y_2|) d(A,B)=max(∣x1−x2∣,∣y1−y2∣)
- 曼哈顿距离与切比雪夫距离的联系
曼哈顿距离 → \to → 切比雪夫距离: ( x , y ) → ( x + y , x − y ) (x,y) \to (x + y,x - y) (x,y)→(x+y,x−y)
切比雪夫距离 → \to → 曼哈顿距离: ( x , y ) → ( x + y 2 , x − y 2 ) (x,y) \to (\dfrac{x + y}{2},\dfrac{x - y}{2}) (x,y)→(2x+y,2x−y)。即旋转 π 4 \frac{\pi}{4} 4π 后缩小一半。
判断
- 点是否在直线上
①
(
Q
−
P
1
)
×
(
P
2
−
P
1
)
=
0
(Q - P_1) \times (P_2 - P_1) = 0
(Q−P1)×(P2−P1)=0
②
Q
Q
Q 在以
P
1
,
P
2
P_1,P_2
P1,P2 为对角顶点的矩形内
- 两线段是否相交
① 快速排斥试验 若两矩形不相交,则线段不相交
② 跨立实验
(
P
1
−
Q
1
)
×
(
Q
2
−
Q
1
)
≥
0
(P_1 - Q_1) \times (Q_2 - Q_1) \ge 0
(P1−Q1)×(Q2−Q1)≥0 和 $ (Q_2 - Q_1) \times (P_2 - Q_1) \ge 0$
- 线段和直线是否相交
只需用跨立实验判断即可。
- 点是否在多边形中
以 p p p 为端点,向左方作射线 L L L,根据交点个数的奇偶性判断。但需要注意与顶点相交、与边重合的特殊情况。
- 线段是否在多边形内
① 两线段端点在多边形内
② 线段与多边形所有边都不内交(两线段相交且交点不在两线段的端点)
做法是求出所有与线段相交的顶点,然后按照 ( x , y ) (x,y) (x,y) 排序,若相邻两点中点均在多边形内,则符合条件。
计算
-
点到线段的最近点
-
计算点到折线/矩形/多边形的最近点
-
计算点到圆的最近距离及交点坐标
-
求线段或直线与圆的交点
均可分为是否与坐标轴平行的两种情况。对于不平行的较复杂情况,通解为联立解方程组然后求出交点。
多边形
- 二维凸包
例题 P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包
① Andrew 算法 用单调栈维护,时间复杂度
O
(
n
log
n
)
O(n \log n)
O(nlogn)。
② Graham 扫描算法 找到左下角的点,然后按极角排序。
- 旋转卡壳
例题 P1452 [USACO03FALL]Beauty Contest G /【模板】旋转卡壳
逆时针枚举凸包边,记录并维护一个当前的最近点(根据叉积计算三角形面积)
- 半平面交
例题 P4196 [CQOI2006]凸多边形 /【模板】半平面交
{ A 1 x + B 1 y + C 1 ≥ 0 A 2 x + B 2 y + C 2 ≥ 0 ⋯ A n x + B n y + C n ≥ 0 \begin{cases} A_1x + B_1y + C_1 \ge 0\\ A_2x + B_2y + C_2 \ge 0\\ \cdots\\ A_nx + B_ny + C_n \ge 0 \end{cases} ⎩ ⎨ ⎧A1x+B1y+C1≥0A2x+B2y+C2≥0⋯Anx+Bny+Cn≥0
S & I S \& I S&I 算法 极角排序,然后维护单调队列(注意先判断队尾再判断队首的情况)
- 平面最近点对
例题 P7883 平面最近点对
分治的思想,以 P m P_m Pm 为界,拆分出点集 A 1 , A 2 A_1,A_2 A1,A2,然后分别找最近点对,距离为 h h h。再找一个点在 A 1 A_1 A1,另一个在 A 2 A_2 A2 的小于 h h h 的点对。最后的时间复杂度为 O ( n log n ) O(n \log n) O(nlogn)。
下午
有关链表的内容。
双向链表
- 插入
data[s] = x;
left[s] = left[p];
right[left[p]] = s;
right[s] = p;
left[p] = s;
- 删除
right[left[p]] = right[p];
left[right[p]] = left[p];
- 恢复
right[left[p]] = p;
left[right[p]] = p;
舞蹈链
一个运用链表到极致的例子。主要步骤如下:
① 矩阵 A A A 为空,返回已解决。
② 选择一列 c c c,通常选择 1 1 1 的个数最少的那一列。
③ a. 若
A
r
,
c
=
1
A_{r,c} = 1
Ar,c=1,说明行
r
r
r 存在,进入 ④;
b. 不存在,回溯,回溯删除,进入 ③ a.。
④ 把 r r r 包含进部分解。
⑤ 对于 ∀ j , A r , j = 1 \forall j,A_{r,j} = 1 ∀j,Ar,j=1,若 ∀ i , A i , j = 1 \forall i,A_{i,j} = 1 ∀i,Ai,j=1,删除第 i i i 行,否则删除第 j j j 行。
⑥ 重复递归。
舞蹈链的思想还可以运用到别的问题中去。我们将矩阵的行的意义为所有的情况,列的意义为约束条件。
- N N N 皇后问题
共有 n 2 n^2 n2 个格子,所以矩阵共有 n 2 n^2 n2 行。而因每行每列每斜行只能有一个皇后的约束条件,所以有 n n n 行 n n n 列, 2 n − 1 2n - 1 2n−1 条主对角线与副对角线,即矩阵共有 6 n − 2 6n - 2 6n−2 列。
- 数独
先分析行,共有 9 × 9 9 \times 9 9×9 个格子,可以填入数字 1 1 1 至 9 9 9,所以共有 9 × 9 × 9 = 729 9 \times 9 \times 9 = 729 9×9×9=729 行。
每一个格子都需要填入数字,所以要有 9 × 9 9 \times 9 9×9 列存放是否已经填入数字的信息。接下去的 3 3 3 个 9 × 9 9 \times 9 9×9 列,分别记录行、列、宫的数字放置情况。所以共需要 4 × 81 = 324 4 \times 81 = 324 4×81=324 列。
跳表
例题 P3103 [USACO14FEB]Airplane Boarding G
跳表可以实现链表中的快速查找,从第一个位置的顶端开始一层层往下跳,直至返回 x x x 不存在。时间复杂度为 O ( log n ) O(\log n) O(logn),空间复杂度为 O ( n ) O(n) O(n)【建立在随机选择插入层的前提下】。
例题选讲
没听的太明白(其实跳表也不是很明白),选几道洛谷上有的题目列一下。
晚上
营员交流,属于是在听天书。几乎属于听不懂的状态,也就当长长见识了 qwq \texttt{qwq} qwq。
今天一天累计算是听了 9 9 9 个多小时,休息去了! Day 2 \texttt{Day 2} Day 2 结束。
Day 3 2022.01.24 \texttt{Day 3 2022.01.24} Day 3 2022.01.24
上午
学习网络流,中午的时候到会议间中又听了听《多重时空下的算法竞赛》。
最大流
算法妙在建立反向边,主要步骤如下:
-
S → T S \to T S→T 找到一条增广路
-
求出流路径中边权最小的值
-
维护路径中的反向边
-
重复操作直到 S S S 与 T T T 不再连通
于是问题就在于如何找增广路,于是有 SAP \textit{SAP} SAP 算法,即重建距离标号,将图分成若干个“层次”。其中包含的两个优化就是弧优化(如果一条边已经被增广过,那么它就没有可能被增广第二次)与断层优化(若图上出现了断层,也就是说无法再找到增广路,则可直接终止算法)。
那么这个算法快在哪里呢?通过探寻本质,只有减少冗余以及重复利用可以有效缩短时间。那么该算法通过距离标号,将原来相互独立的增广路相互联系,从而重复利用来节省时间。
费用流
下午
发现自己学过 tarjan 了,于是想就听听数据结构选讲。但一打开课件就发现都是什么
IOI
\texttt{IOI}
IOI 黑题,劝退了……还是听 tarjan 吧!
求 LCA \texttt{LCA} LCA
若 LCA ( u , v ) = k \texttt{LCA }(u,v) = k LCA (u,v)=k,当遍历完 u u u 所在子树后, u u u 所在子树所有的结点跟 k k k 其它子树所有结点的 LCA \texttt{LCA} LCA 一定为 k k k。可以通过并查集维护。伪代码大概如下:
fa[v] = v;vis[v] = 1;
for (i...)
if (!vis[i]) dfs (i),fa[i] = v;
for (v...)
if (vis[u]) LCA[u][v] = LCA[v][u] = get_fa (u);
若 LCA ( u , v ) = u \texttt{LCA }(u,v) = u LCA (u,v)=u,在结点 u u u 信息返回前, u u u 结点子树均已访问完,故伪代码此时仍然成立。
题面中强调不存在环,故这是一棵树。考虑树上差分,则有 d i s i , j min = d e p i + d e p j − 2 d e p L C A ( i , j ) dis_{i,j}{\min} = dep_i + dep_j - 2dep_{LCA(i,j)} disi,jmin=depi+depj−2depLCA(i,j)。
求割点
若 u u u 为生成树的根,则 u u u 为割点的充要条件是 u u u 的子树 ≥ 2 \ge 2 ≥2。
若 u u u 不为生成树的根,则 u u u 为割点的充要条件是在 v v v 或 v v v 子孙结点和 u u u 祖先结点不存在回边。
可以使用时间戳来记录深度优先数与最低深度,有:
l o w [ u ] = min { d f n [ u ] min ( l o w [ v ] ∣ v is children ) min ( d f n [ u ] ∣ ( u , v ) is cross edge ) low[u] = \min \begin{cases} dfn[u]\\ \min{(low[v]\mid v \texttt{ is children})}\\ \min{(dfn[u]\mid (u,v) \texttt{ is cross edge})} \end{cases} low[u]=min⎩ ⎨ ⎧dfn[u]min(low[v]∣v is children)min(dfn[u]∣(u,v) is cross edge)
若 u u u 存在一个孩子 v v v 使得 d f n [ u ] ≤ l o w [ v ] dfn[u] \le low[v] dfn[u]≤low[v],则 u u u 为割点。
割边
若 ( u , v ) (u,v) (u,v) 为割边的充要条件是 u → v u \to v u→v 不为重边且 v v v 或 v v v 的子孙结点中没有指向 u u u 或 u u u 祖先的回边。若 d f n [ u ] < l o w [ u ] dfn[u] < low[u] dfn[u]<low[u],则 ( u , v ) (u,v) (u,v) 为割边(与割点思想类似)。
辨析:
- 两割点之间的边一定为割边。
错误!反例如下:
A-B
| |
C-D
| |
E F
C , D C,D C,D 为割点,但 ( C , D ) (C,D) (C,D) 不为割边。
- 割边的两端点均为割点。
错误!反例如下:
A-B-C
( A , B ) (A,B) (A,B) 为割边,但 A A A 不为割点。
若 v v v 为割点 -> 子树中存在 b b b -> 所求之点
关键在于判断子树中是否存在 b b b,可以通过 d f n [ u ] dfn[u] dfn[u] 判定。若 d f n [ u ] < d f n [ b ] dfn[u] < dfn[b] dfn[u]<dfn[b],则符合条件。
例题 P7687 [CEOI2005] Critical Network Lines
课后补题,解析见我的博文 【题解】P7687 [CEOI2005] Critical Network Lines 。
强连通分量
注意,求割点与割边是在无向图中,而强连通分量是在有向图中,要注意区分。
若 l o w [ u ] < d f n [ u ] low[u] < dfn[u] low[u]<dfn[u],则子孙结点能连到自己上方的结点;若 d f n [ u ] = d f n [ u ] dfn[u] = dfn[u] dfn[u]=dfn[u],则 u u u 为根,内部仍存在一个或多个强连通分量,递归求解即可。
当 l o w [ u ] = d f n [ u ] low[u] = dfn[u] low[u]=dfn[u] 为结束条件进行弹栈得到强连通分量。
例题 P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G
差不多可以说是板子题,缩点后判断是否只有 1 1 1 个出度为 0 0 0 的点。
晚上
趁着晚饭后做了课上讲的一道题,并写了篇题解。
还是营员交流,还是属于听不懂的状态。
Day 3 \texttt{Day 3} Day 3 结束。
Day 4 2022.01.25 \texttt{Day 4 2022.01.25} Day 4 2022.01.25
上午
数据结构中的复杂树问题,收获巨大!!!重点主要放在了前三个中,后面基本属于提了提。
树链剖分
轻重链剖分。一个定义就是重子结点表示其子结点中子树最大的子结点。
- 性质
① 在每条重链结点的 dfn 连续,即优先选择重子结点。
② 每个子树内的 dfn 连续。
③ 向下经过一条轻边,子树大小至少减半,不超过
log
n
\log n
logn 条重链。
④ 重链开头不一定为重子结点。
- 建树过程
void dfs1 (int u,int fa)
{
sz[u] = 1;f[u] = fa;dep[u] = dep[fa] + 1;
for (int i = head[u];i;i = nxt[i])
{
int v = to[i];
if (v != fa)
{
dfs1 (v,u);
sz[u] += sz[v];
if (sz[v] > sz[hson[u]]) hson[u] = v;//求重儿子
}
}
}
- 树的分解
void dfs2 (int u,int fa)
{
if (hson[u])//优先走重边
{
seg[hson[u]] = ++seg[0];
top[hson[u]] = top[u];//重链的顶端
rev[seg[0]] = hson[u];
dfs2 (hson[u],u);
}
for (int i = head[u];i;i = nxt[i])
{
int v = to[i];
if (!top[v])
{
seg[v] = ++seg[0];
rev[seg[0]] = v;
top[v] = v;//此时 (u,v) 为轻边,v 为所在重链的顶端
dfs2 (v,u);
}
}
}
P3384 【模板】轻重链剖分/树链剖分 模板题。
通过向上跳来维护信息。若在重链上,则跳到顶端;若不在则在其顶端向上跳一步至重链。直到两点均在同一条重链上即可。核心代码如下:
void ask (int u,int v)
{
int fx = top[u],fy = top[v];
while (fx != fy)
{
if (dep[fx] < dep[fy]) swap (u,v),swap (fx,fy);//深度大的向上跳
query (1,1,seg[0],seg[fx],seg[u]);
u = f[fx],fx = top[u];
}
if (dep[u] > dep[v]) swap (u,v);
query (1,1,seg[0],seg[u],seg[v]);//在同一条重链上的不同位置,最后需将这一段区间也进行求解
}
再放一道练手的题目,几乎也是裸题。
支持两种操作,树上的区间修改与子树的修改。注意因为涉及
0
0
0 和
1
1
1 两种情况,因此打懒标记的时候需要注意一下 if (tmp[cur] == -1) return ;,当然忽略这个语句就不存在这个问题了。
伸展树 splay \texttt{splay} splay
均摊时间复杂度为 O ( log n ) O(\log n) O(logn),通过势能分析可以得证。伸展树有一个性质,就是中序遍历不会改变。
-
右旋
zig(x)
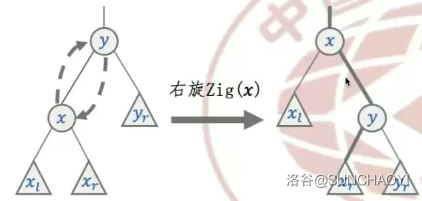
-
左旋
zag(x)
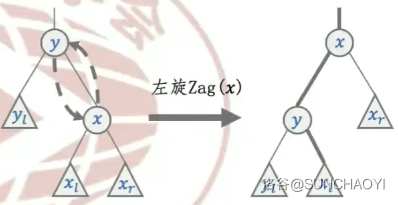
-
rotate函数 -
splay函数 -
插入
-
查找
-
分裂
-
合并
-
删除
-
找寻排名为 k k k 的数
-
区间删除
下午
还是听《新版 NOI-Linux \texttt{NOI-Linux} NOI-Linux 系统使用》比较实用叭。
在电脑上成功装了一个 NOI-Linux \texttt{NOI-Linux} NOI-Linux 虚拟机,针不戳。捣鼓了一下午的虚拟机,效果如下:
非常好!~~~
Day 4 \texttt{Day 4} Day 4 结束。
Day 5 2022.01.26 \texttt{Day 5 2022.01.26} Day 5 2022.01.26
上午
听 IOI \texttt{IOI} IOI 命题方向。只是停留在听听的层面,但不得不说交互题和构造题等非传统题可以说是兴起了。还看到了一些“恶搞题”,印象最深的就是:
- 人工智能题?面向数据才是真理!
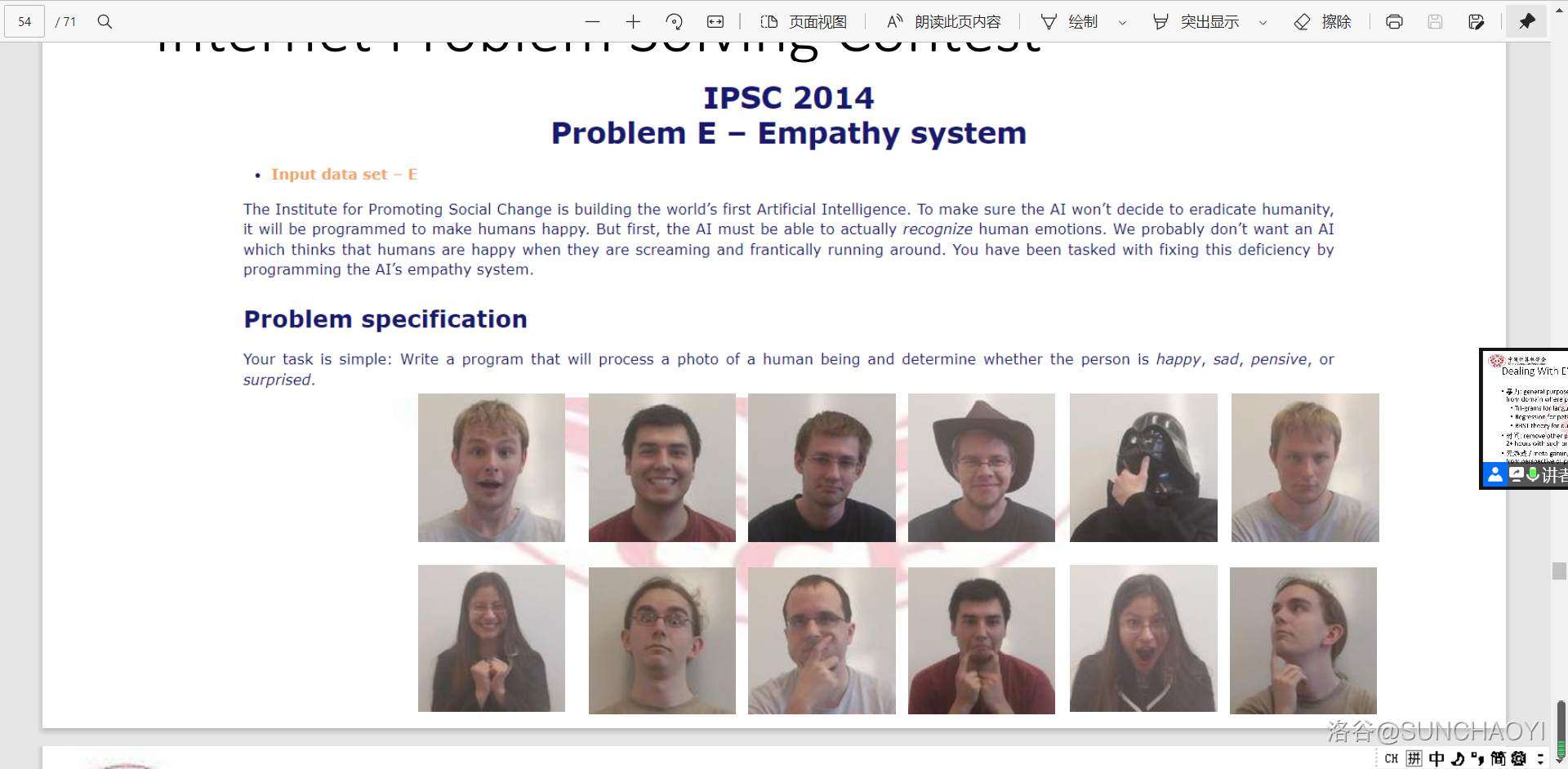
MoMOOMoo题
好像有个营员因“不文明语言”被管理员踢了…害怕
.jpg
\texttt{.jpg}
.jpg
下午
应该是冬令营的最后一节课了 awa \texttt{awa} awa,题目选讲,听听神仙是怎么爆切 IOI \texttt{IOI} IOI 的叭。
似乎今天 15 : 30 15:30 15:30 就结束了哈,明天结营测试, RP++ \texttt{RP++} RP++ 吧!
晚上
试机,没啥大问题。
Day 5 \texttt{Day 5} Day 5 结束。
Day 6 2022.01.27 \texttt{Day 6 2022.01.27} Day 6 2022.01.27
两道传统题,一道交互题。先开了 T2 \texttt{T2} T2,用空间换时间打了一个 O ( n m ) O(nm) O(nm)。然后发现啥都不会,交互题主要之前没有做过,所以就不太会格式,最后应该 CE \texttt{CE} CE 了。想着这样肯定也就不能拿牌,所以 T1 \texttt{T1} T1 的 25 pts \texttt{25 pts} 25 pts 最后也没拿。
Day 7 2022.01.28 \texttt{Day 7 2022.01.28} Day 7 2022.01.28 很后悔没打那个暴力,果然 Fe \texttt{Fe} Fe 了,被卡线 qwq \texttt{qwq} qwq。





















 943
943

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








