二分法总是学不透！

1. 二分法易错点

（1）while循环语句中的判断条件怎么写
（2）更新区间时选择mid还是mid-1

2.在二分过程中对区间边界的选择要保持不变

 一开始为左闭右闭，则在变化过程中也应该始终保持左闭右闭。

3.左闭右闭区间——[1,1]区间合法

left=0;
right=max-1;    //搜索区间：[0,max-1] 搜索值：值为target的数组下标
while(left<=mid){
    mid=l+(r-l)/2;
    if(num[mid]>target) right=mid-1;  
    //此时要更新左区间的右边界 而右边界会包含在区间中，
    //因此我们mid-1（不需要再计算一次mid了）
    else if(num[mid]<target) left=mid+1;
    else return mid;
}

4.左闭右开区间——[1,1)区间不合法

left=0;
right=max;    //搜索区间：[0,max) 搜索值：值为target的下标
while(left<mid){
    mid=l+(r-l)/2;   //防溢出
    if(num[mid]>target) right=mid;     
    //此时要更新左区间的右边界 而右边界不会包含在区间中，因此我们mid即可
    else if(num[mid]<target) left=mid+1;
    else return mid;
}

5.变形

（1）简单二分+循环数组 
（2）存在重复元素（找第一次/最后一次出现target的位置）
    第一次：在相等时进一步判断是不是第一个——只需要判断前一个元素是否为target
    若前一个也是target，则移动右指针 right=mid-1
    最后一次：判断后一个元素，移动左指针 left=mid+1

6.时间复杂度：O（log n）

7.进一步理解二分法

我们要找到蓝红边界即求出未知数k，在一开始整个数组都是灰色的。

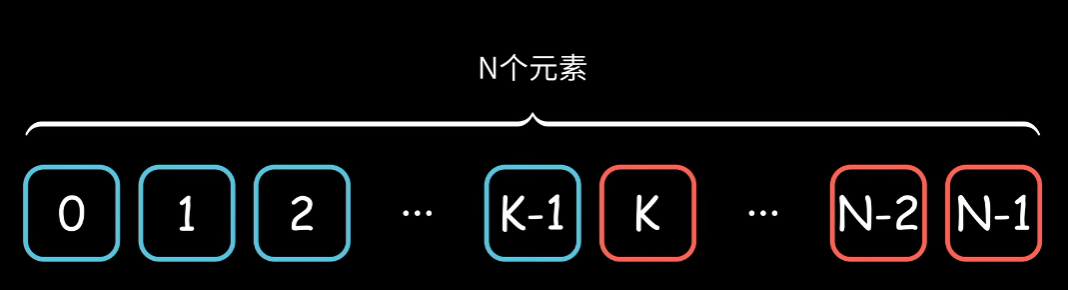
朴素算法：设置指针从头或从尾开始遍历   O(n)
二分：判断区间中点的颜色并不断更新区间来找到边界

伪代码：
l=-1,r=N      //l指向蓝色区域，r指向红色区域
while l+1!=r
   m= [(l+r)/2]
   if IsBlue(m) l=m
   else r=m    //l、r快速向蓝红边界逼近，保持l、r颜色不变
return l or r  //最后，l、r刚好指向蓝红边界

五点七边

几个细节问题：

（1）为什么l的初始值为-1，r的初始值为N？
能不能让l的初始值为1或r的初始值为N-1？ 不可以
当全红或全蓝时会出问题。

（2）m是否始终处于[0,N)以内？
只有当m处于这个区间时才位于数组内部。（考虑当l、r分别取最小或最大时）
m的最小值：（-1+1）/2=0 [为什么不是-1和0？ 因为当r=0时会满足l+1=r 退出循环]
m的最大值：（N-2+N）/2=N-1
（3）更新指针时，能不能写成l=m+1，或者r=m-1？
会在细节上出错！
当在某次循环中，m已经位于蓝（红）色的边缘，如果我们让l=m+1会直接变成红（蓝）色
（4）程序会不会陷入死循环？

一般流程

（1）建模，分成蓝色与红色
（2）判断返回值是l还是r
（3）由模板写出代码

8.题目

（1）借教室

输入：
第一行包含两个正整数 n,m，表示天数和订单的数量。 
第二行包含 n个正整数，其中第 i 个数表示第 i 天可用于租借的教室数量。 
接下来有 m 行，每行包含三个正整数，表示租借的数量，租借开始、结束分别在第几天。 
每行相邻的两个数之间均用一个空格隔开。
天数与订单均用从 1 开始的整数编号。

输出：
如果所有订单均可满足，则输出只有一行，包含一个整数 0 。
否则（订单无法完全满足）输出两行，第一行输出一个负整数 −1 ，第二行输出需要修改订单的申请人编号。

思路分析：差分法+二分法
*二分法如何考虑？
 a.我们先划分蓝红区域——能够完成的订单为蓝色，不能完成的订单为红色
 b.之后我们要返回红色的边界点（也就是r=l+1）
 c.套用算法模板

l=0,r=N+1    
while l+1!=r
    m= [(l+r)/2]
    if IsBlue(m) l=m
    else r=m   
return  r  

#include<iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1000000;
int m,n;
int r[N];
LL use[N];
struct Order {
    int d;  
    int s;  
    int e;  
};
Order orders[N];

bool check(int mid){
    memset(use, 0, sizeof use);  //初始化差分数组为0
    for (int i = 1; i <= mid; i++) {
        use[orders[i].s] += orders[i].d; 
        use[orders[i].e + 1] -= orders[i].d;  
    }

    for (int i = 1; i <= n; i++) {
        use[i] += use[i - 1];    //求出前缀和
        if (use[i] > r[i]) return false; //如果哪一天的教室需求量超了，则返回false
    }

    return true; 
}

int main(){
    //依次输入天数、教室数及订单数
    cin >> n >> m;
    for(int i=1;i<=n;i++) cin >> r[i];
    for(int i=1;i<=m;i++) cin >> orders[i].d >> orders[i].s >> orders[i].e;

    //划定蓝红区域，开始二分查找边界
    int l=0,r=m+1;
    while (l+1 != r) {
        int mid = (r+l+1) / 2; 
        if (check(mid)) l = mid; //如果mid个订单是教室够，则更新左边界
        else r = mid; 
    }

    if (r>m) cout << "0";  //当订单全部都可以完成时，右边界应该始终为m+1
    else cout << "-1" << endl << r;  

    return 0;
}

Let’go 借教室!

（2）分巧克力

小明一共有 N 块巧克力，其中第 i 块是 $H_i\times W_i$ 的方格组成的长方形。
为了公平起见，小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。
切出的巧克力需要满足：形状是正方形，边长是整数 + 大小相同

输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行包含两个整数 $H_i和W_i$。
输入保证每位小朋友至少能获得一块 1×1 的巧克力。

输出格式
输出切出的正方形巧克力最大可能的边长。

log 10⁶=16

思路分析：
首先考虑最大的边长有多大——能够切割的最大边长一定小于等于所给巧克力的最小边
之后可以使用二分法找出这个最大边
    即l=0，r=N(大边),对每个mid判断是否满足能够切出k块mid长的的正方形
也就是说，该题的蓝色区域为该边长可以切出k块，红色区域为该边长不能切成k块
    最大可能的边长即为蓝色的边界，即返回值为l（r+1）

#include<iostream>
using namespace std;

typedef long long ll;
const int N=100000;
int n,k;
ll a[N],b[N];
int max_edge=0;
int prefix[N];

bool check(int mid){
    for(int i=0;i<n;i++){
        prefix[i]=(a[i]/mid)*(b[i]/mid);
        prefix[i]+=prefix[i-1];
    } //prefix数组接收每块巧克力切mid长的正方形的个数 之后再前缀和相加
    if(prefix[n-1]<k) return false; //总共巧克力数小于k，则返回false
    else return true;
    
}

int main(){
    //输入数据
    cin >> n >> k;
    for(int i=0;i<n;i++) {
        cin >> a[i] >> b[i];
        int max=(a[i]<b[i])?b[i]:a[i];
        max_edge=(max_edge<max)?max:max_edge;
        //先找出巧克力的最大边，右边界即为最大边
        //why不是最小边？  当巧克力足够多时边很小的巧克力可以不使用
    }
    
    int l=0,r=max_edge+1; //定义边界情况
    while(l+1!=r){
        int mid = (l+r+1)/2;
        if(check(mid)) l=mid; //mid为边时若不满足，则更新左边界
        else r=mid;
    }
    
    cout << l;
    
    return 0;
}

Let’go 分巧克力!

（3）管道

有一根长度为 len 的横向的管道，该管道按照单位长度分为 len 段，
每一段的中央有一个可开关的阀门和一个检测水流的传感器。
一开始管道是空的，位于 Li 的阀门会在 Si 时刻打开，并不断让水流入管道。
对于位于 Li 的阀门，它流入的水在 Ti（Ti≥Si）时刻会使得从第 Li−(Ti−Si)
段到第 Li+(Ti−Si) 段的传感器检测到水流。
求管道中每一段中间的传感器都检测到有水流的最早时间。

---

输入格式
输入的第一行包含两个整数 n,len，分别表示会打开的阀门数和管道长度。
接下来 n 行每行包含两个整数 $L_i,S_i$，用一个空格分隔
表示位于第 $L_i$ 段管道中央的阀门会在 $S_i$ 时刻打开。

输出格式
输出一行包含一个整数表示答案。

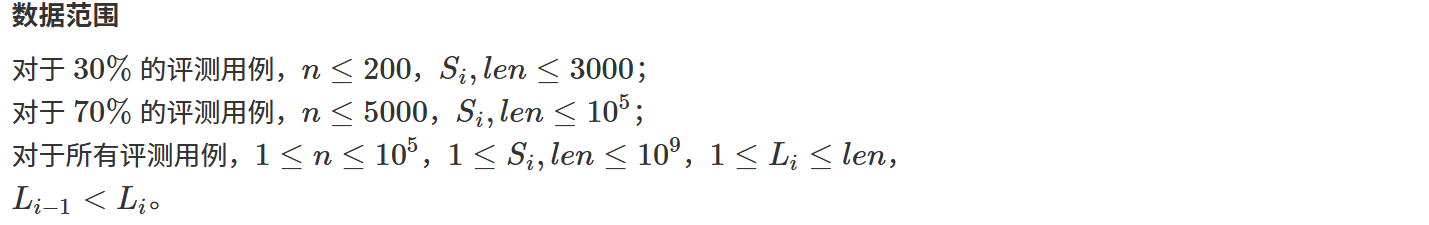
思路分析：

遇到的问题：
（1）在取二分右边界时，由于$S_i$最大值可以取到 $10^9$，则我们需要设置一个变量2e9（1e9可能会溢出，稳妥一点稍大设置吧）
（2）在设置数组时，如果是全局数组，则N不能过大
（3）此题要求的是最大值，因此
if (!check(mid)) left = mid; //当mid时刻不满足时才更新左边界
else right = mid;

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

typedef long long ll;
const int N=100000;
ll n, len;
int l[N],s[N];

bool check(ll mid) {
    vector<pair<ll, ll>> a;
    for (int i = 0; i < n; i++) {
        if (mid < s[i]) continue;
        ll left = l[i] - (mid - s[i]);
        ll right = l[i] + (mid - s[i]);
        left = max(left, 1LL);
        right = min(right, len);
        a.emplace_back(left, right);
    }

    sort(a.begin(), a.end());

    ll covered = 0;
    for (int i = 0; i < a.size(); i++) {
        if (a[i].first > covered + 1) return false;
        covered = max(covered, a[i].second);
        if (covered >= len) return true;
    }

    return covered >= len;
}

int main() {
    cin >> n >> len;
    for (ll i = 0; i < n; i++) cin >> l[i] >> s[i];

    ll left = -1, right = 2e9;
    while (left + 1 != right) {
        ll mid = (left + right + 1) / 2;
        if (!check(mid)) left = mid;
        else right = mid;
    }

    cout << right;
    return 0;
}

（4）技能升级

小蓝最近正在玩一款 RPG 游戏。他的角色一共有 N 个可以加攻击力的技能。其中第 i 个技能首次升级可以提升 $A_i$点攻击力，以后每次升级增加的点数都会减少 $B_i$。
$\frac{A_i}{B_i}$（向上取整）次之后，再升级该技能将不会改变攻击力。
现在小蓝可以总计升级 M 次技能，他可以任意选择升级的技能和次数。
请你计算小蓝最多可以提高多少点攻击力？

输入格式
输入第一行包含两个整数 N 和 M。
以下 N 行每行包含两个整数 $A_i$ 和 $B_i$。

输出格式
输出一行包含一个整数表示答案。

思路分析
1.首先确定红蓝边界，要求的是总的最高的攻击力，我们可以先求出单次升级能够达到的最小攻击增值t，之后再遍历求和求出总值，即我们可以设蓝色区域为增加攻击不大于t，红色为小于t，只需要判断当达到该攻击增值之时已经升级的次数是否等于M即可
2.返回值为蓝色区域的边界即l
3.l=-1,r=N (最小攻击从0开始，最大攻击设置为1e9)

即有n个等差数列，首项为$a[i]$,公差为$-b[i]$。
对于每个技能，能够升级的最大次数是$\frac{a[i]-1}{b[i]+1}$，通过遍历我们可以计算出最多能够升级的的次数count；
若$m>count$，则总共升级次数m=count（即$m$应该取输入$m$与计算出$count$的最小值）。
之后，我们通过二分法计算出蓝色边界l；
升级t次时增加的攻击值为:
$$a[i]-(t-1)\ast b[i]$$
升级t次总共增加的攻击值为：
$$t\ast a[i]-b[i]\ast (t-1)\ast t/2$$

则我们可以计算出当攻击力增值不小于l时升级的次数及对应的攻击增量总数：

#include <iostream>
using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

ll a[N], b[N]; 
ll n, m;

bool check(int x)
{
    ll sum = 0;
    for (int i = 1; i <= n; i++)
    {
        if (a[i] >= x)
        {
            sum += (a[i] - x) / b[i] + 1;
        }
    }
    return sum >= m;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);

    ll tot = 0;
    cin >> n >> m;

    for (int i = 1; i <= n; i++)
    {
        cin >> a[i] >> b[i];
        tot += (a[i] - 1) / b[i] + 1;
    }

    m = min(m, tot);
    ll ans = 0;
    ll l = -1, r = 2e9;
    while (l+1 != r)
    {
        ll mid = (l+r+1)/2;
        if (check(mid)) l = mid ;
        else r = mid;
    }
    ll count=0;
    for (int i = 1; i <= n; i++)
    {
        ll t = (a[i] - l) / b[i] + 1;
        if (t <= 0 || a[i] < l)  continue;  //特殊情况 跳过该循环
        if (a[i] - (t - 1) * b[i] == l)  t--;  //从t里面把等于l的情况删掉
        ans += t * a[i] - (t * (t - 1) / 2 * b[i]);
        count+=t;
    }

    cout << ans + (m - count) * l << endl;
    return 0;
}

Let’s go 技能升级

（5）冶炼金属

我觉得这题不用二分法更好解。

小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X 。
这个炉子有一个称作转换率的属性 V ，V 是一个正整数，这意味着消耗 V 个普通金属 O 恰好可以冶炼出一个特殊金属 X ，当普通金属 O 的数目不足 V 时，无法继续冶炼。
现在给出了 N 条冶炼记录，每条记录中包含两个整数 A 和 B，这表示本次投入了 A 个普通金属 O ，最终冶炼出了 B 个特殊金属 X 。
每条记录都是独立的，这意味着上一次没消耗完的普通金属 O 不会累加到下一次的冶炼当中。
根据这 N 条冶炼记录，请你推测出转换率 V 的最小值和最大值分别可能是多少，题目保证评测数据不存在无解的情况。

输入格式
第一行一个整数 N ，表示冶炼记录的数目。
接下来输入 N 行，每行两个整数 A、B，含义如题目所述。

输出格式
输出两个整数，分别表示 V 可能的最小值和最大值，中间用空格分开。

数据范围
对于 30% 的评测用例，$1\le N\le 10^2$。
对于 60% 的评测用例，$1\le N\le 10^3$。
对于 100% 的评测用例，$1\le N\le 10^4，1\le B\le A\le 10^9$。

//使用数学方法
#include<iostream>
using namespace std;

typedef long long ll;
const int N=10010;
int n;
ll a[N],k[N];
ll r_max=0,l_min=1e9;

int main(){
    cin >> n;
    for(int i=0;i<n;i++){
        cin >> a[i] >> k[i];
        if (k[i] == 0) continue;
        l_min=(l_min<a[i]/k[i])?l_min:a[i]/k[i];
        r_max=(r_max>a[i]/(k[i]+1))?r_max:a[i]/(k[i]+1);
    }
    
    cout << r_max+1 << " " << l_min;
    
    return 0;
}

Let’t go 冶炼金属

（6）最佳牛围栏

农夫约翰的农场由 N 块田地组成，每块地里都有一定数量的牛，其数量不会少于 1 头，也不会超过 2000 头。
约翰希望用围栏将一部分连续的田地围起来，并使得围起来的区域内每块地包含的牛的数量的平均值达到最大。
围起区域内至少需要包含 F 块地，其中 F 会在输入中给出。
在给定条件下，计算围起区域内每块地包含的牛的数量的平均值可能的最大值是多少。

输入格式
第一行输入整数 N 和 F ，数据间用空格隔开。
接下来 N 行，每行输入一个整数，第 i+1 行输入的整数代表第 i 片区域内包含的牛的数目。

输出格式
输出一个整数，表示平均值的最大值乘以 1000 再向下取整之后得到的结果。

数据范围
$1\le N\le 100000$
$1\le F\le N$

思路分析

1. 题目抽象：给你一组长度为 $n$ 的整数数组 $cow[]$，问是否存在一个长度为 $m$ 的子数组，它的平均值 ≥ 某个值 x。
2. 我们把目的反过来：找到一个最大的平均值，使$cow[]$数组中存在一个长度为$m$的子数组。
   这个时候我们可以使用二分法。
3. 🔍对每个mid，是否存在一个长度 ≥ $m$ 的子数组，平均值 ≥ mid？
   这个问题 可以转化为：$\frac{a_i+...+a_j}{j-i+1}$是否满足≥ $mid$?
   即$$a_i+\dots +a_j\ge (j-i+1)\ast mid$$
   即 $$(a_i-mid)+\dots +(a_j-mid)\ge 0$$

所以我们把数组每一项都减去 mid，问题就变成：是否存在一段长度 ≥ m 的子数组，和 ≥ 0？

4. 那我们的思路就清晰了：
   （1） 先输入数组$cow[]$
   （2） 利用二分法找出存在长度为$m$的子数组的最大数组平均值mid，也就是说蓝色区域为存在子数组长度小于 $m$，红色区域为不存在子数组长度大小等于$m$；
   l=-1,r=N;
   返回值为蓝色区域边界
   （3）在check()函数里，我们将问题转化为求子数组的和是否大于等于0，则我们可以使用前缀和数组求解。

注意点：由于本题在二分时以平均值为标度来开展，因此与之前二分法不同的是类型变成了double双精度

 while (r - l > 1e-5) {  //判断条件  1e-5为精度要求（尽量小）
        double mid = (l + r) / 2;
        if (check(mid)) l = mid;
        else r = mid;
    }

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 100005;
int n, m;
int cow[N];
double sum[N]; // 前缀和数组

bool check(double mid) {
    // 构造前缀和数组，注意 sum[0] = 0
    sum[0] = 0;
    for (int i = 1; i <= n; i++) {
        sum[i] = sum[i - 1] + (cow[i - 1] - mid);
    }

    double minv = 0;
    for (int i = m; i <= n; i++) {
        minv = min(minv, sum[i - m]);
        if (sum[i] - minv >= 0) return true;
    }
    return false;
}

int main() {
    cin >> n >> m;
    double l = 0, r = 0;
    for (int i = 0; i < n; i++) {
        cin >> cow[i];
        r = max(r, (double)cow[i]); // 二分上限为最大值
    }

    while (r - l > 1e-5) {
        double mid = (l + r) / 2;
        if (check(mid)) l = mid;
        else r = mid;
    }

    cout << (int)(r * 1000) << endl;
    return 0;
}

Let’s go 最佳牛围栏