光照模型在计算机图形学中的应用

scott198512

已于 2025-04-16 11:57:58 修改

阅读量1.1k

点赞数 10

CC 4.0 BY-SA版权

分类专栏： 3D重建-生成式-世界模型文章标签：三维重建图形渲染图形学

于 2025-04-08 21:01:49 首次发布

本文链接：https://blog.youkuaiyun.com/scott198510/article/details/147076901

1.概述

用特定材料制成的物体，在视野中显示出来的外观效果取决于材料与场景中光线之间复杂的相互作用。在本篇中，将探讨材料属性的几个关键方面，重点关注局部相互作用，并深入研究一些经典的光照模型（反射模型）来捕捉这些属性。

2.人眼是如何看见物体

看物体的过程涉及我们的眼睛接收光能，然后将其传输到我们的大脑。人眼由多层组成，其中一层是视网膜，其中包含感知可见光的感光细胞。

这种细胞主要有两种类型：视杆细胞和视锥细胞。视杆细胞对光子高度敏感，甚至一个光子就能触发它。这类细胞提供有关光强度的信息。另一方面，视锥细胞负责颜色感知。视锥细胞也有三种类型，每种类型对不同的波长作出反应，分别对应红色、绿色和蓝色。通常将这些颜色称为原色。

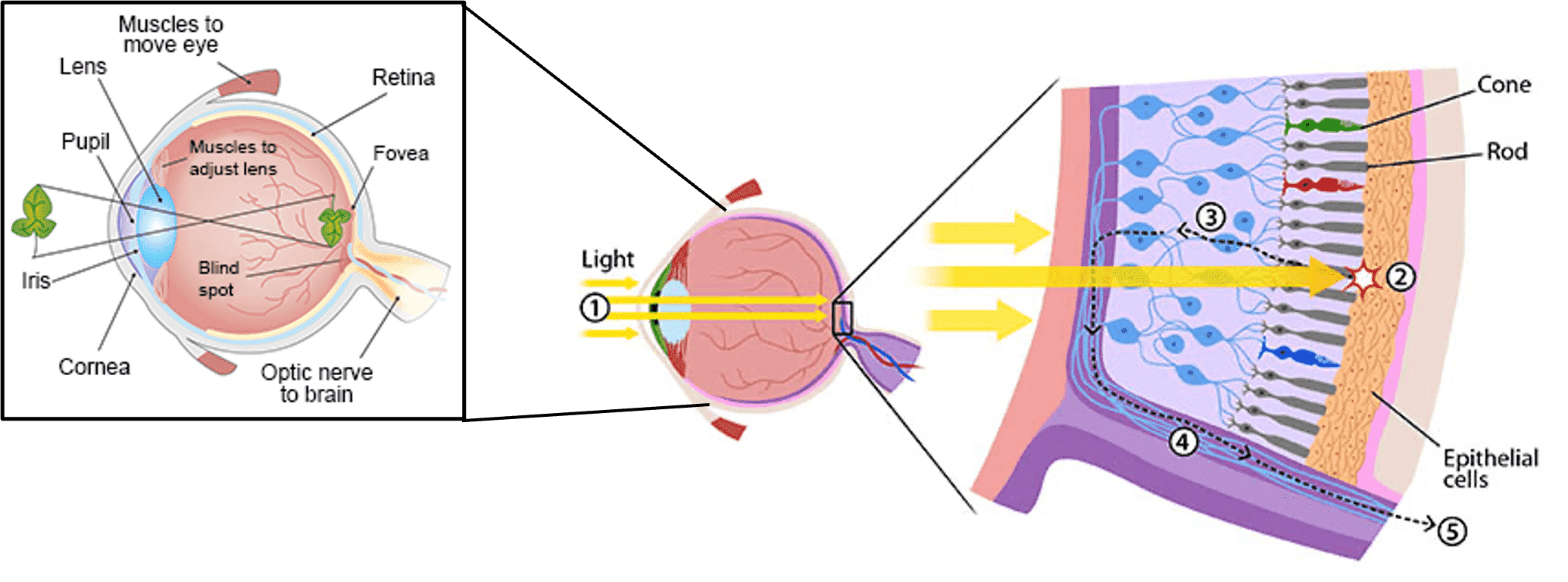
图 1.人类眼睛的解剖结构（参考资料4）

事实上，颜色并非天生存在。相反，我们的大脑会根据眼睛中三种视锥细胞的响应水平来重建颜色。人眼只能对这些电磁波光谱的一部分做出响应，通常称为可见光。可见光指的是波长在 400nm 至 700 nm 范围内的光。

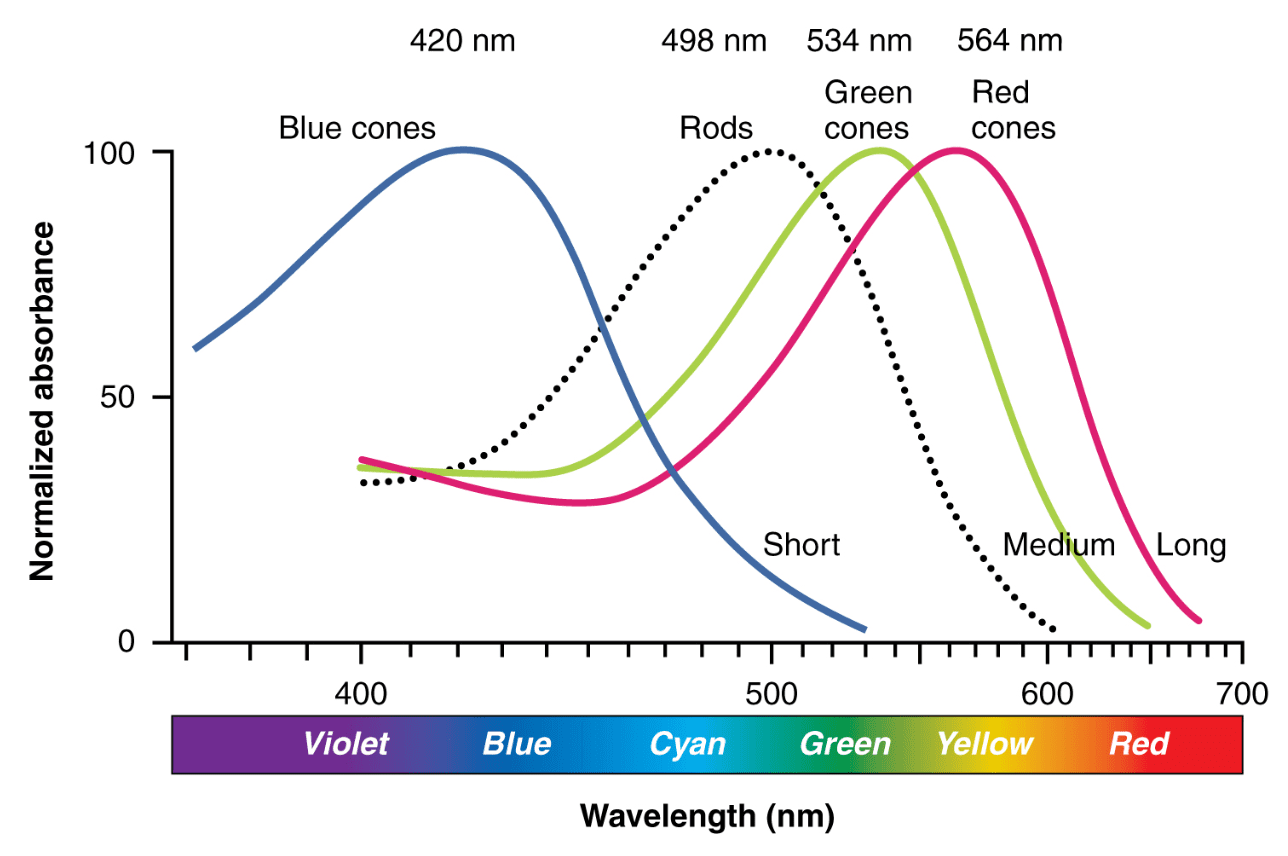
图 2.视杆细胞和视锥细胞的反应水平（参考资料4）

那么光是如何与材料相互作用的呢？这个过程可以用量子物理学来解释，但本篇文章只提供了这个过程的高度概述。当一种材料或原子接收到一个光子时，它会进入激发态。随后，它会恢复到正常状态，将能量释放到周围空间。这种能量的释放导致了光的反射、吸收和透射等各种现象。

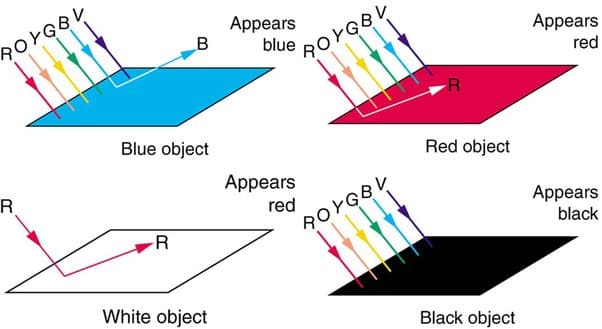
图 3.白光与物体的相互作用

因此，计算机图形学中的真实色彩表现需要量化光和材料，制定描述它们相互作用的规则，并通过某种显示介质呈现结果，从而产生正确的感知。光照模型，也称为反射模型或阴影模型，通过考虑光和物体表面接触点的局部特性来计算表面上点的颜色。

此类反射模型从光栅化系统时代（光线追踪技术之前）就已经开始使用，不过当时仅使用了一些特定模型，如镜面反射、漫反射及其组合形式（Phong着色模型）。而下文即将探讨的，双向反射分布函数（BRDF）是一种通用数学框架，能够统一表征所有这些特定反射模型。

3.表面相互作用：BxDF 函数

我们将要讨论的反射模型在渲染方程之前就已被应用于光栅化系统中，当时仅使用了一些特定的模型，如镜面反射、漫反射及其组合形式（Phong着色模型）。在这里，BRDF 充当能够表示所有这些不同反射模型的通用公式。

在本节中，我们将深入研究其他类型的双向分布函数，这些函数对于表征光与表面的相互作用很有帮助。

3.1 BTDF

当光线照射到物体表面时，部分光线会被反射，部分光线会被材料吸收，部分光线会被透射，也就是说光线会完全穿过材料。表面的双向透射分布函数 (BTDF)表示为：

$f_t (\mathrm{p}, \omega_{\mathrm{i}}, \omega_{\mathrm{t}})$

其中， $w_i,w_t$ 分别位于表面 $p_i$ 的相对半球空间，描述了透射光的分布情况。

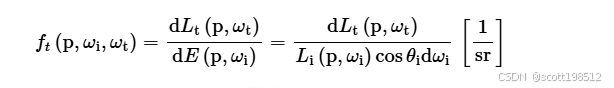
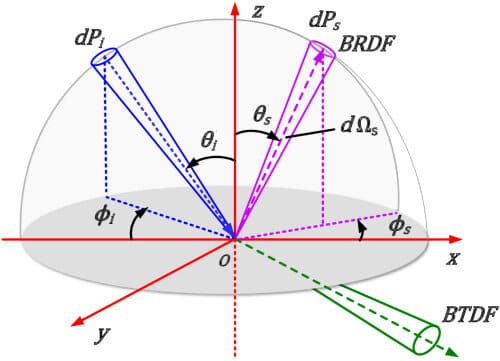
图 4.BRDF 和 BTDF 定义的几何形状 ( ResearchGate )

3.2 BSDF

为了便于在方程中表示，我们通常将 BRDF 和 BTDF 一起表示为：

$f(\mathrm{p}, \omega_{\mathrm{i}}, \omega_{\mathrm{o}})$

将其命名为双向散射分布函数（BSDF），即：

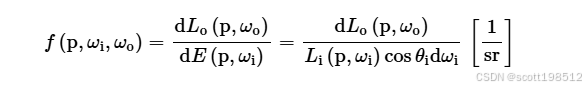
根据定义，我们可以对 p 点周围入射方向球面上的出射辐射度微分进行积分，计算出方向 $w_o$ 上的的出射辐射度：

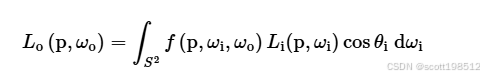
当积分域为上述球面 $S^2$ 时，该方程通常称为散射方程；当积分域限定在上半球面 $H^2$ 范围时，则称为反射方程。这一方程作为描述光线在表面散射行为的通用数学函数。在实际应用中通常被分解为反射分量（BRDF）和透射分量（BTDF）两部分。

上述BSDF 的定义还不是很规范，更多详尽说明，需参阅 Wikipedia-BSDF。

3.3 BSSRDF

半透明表面的反射现象更为复杂；从皮肤、树叶到蜡质和液体等多种材料都表现出次表面散射（也称为次表面光传输）的特性，即光线从表面某点射入材料内部，经过多次散射后，最终从另一点传出表面。

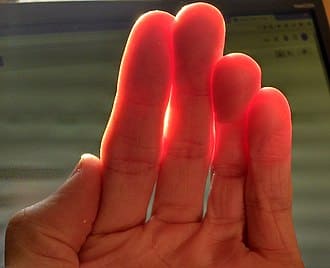
图 5.人手中的次表面散射（维基百科-次表面散射）

假设一束光线在表面点 $p_i$ 处入射，经过材质内部的多次反射后，最终从 $p_i$ 附近的另一点 $p_o$ 出射，这种散射可以通过双向表面散射反射分布函数 (BSSRDF) $S(\mathrm{p}_{\mathrm{i}}, \omega_{\mathrm{i}}, \mathrm{p}_{\mathrm{o}}, \omega_{\mathrm{o}})$ 来表示：

BSSRDF 定义为：在方向 $w_o$ 上点 $p_o$ 处的出射微分辐射度与来自方向 $w_i$ 的点 $p_i$ 的入射微分通量之比：

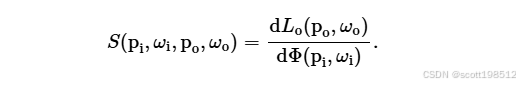
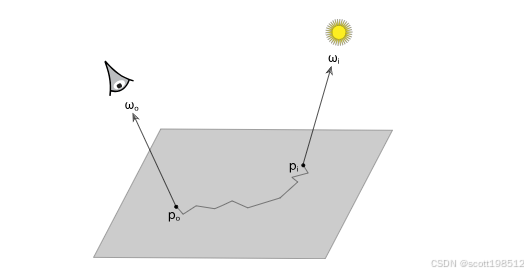
图 6. BSSRDF 的几何形状（参考资料3）

显然，BSSRDF 需要对散射方程进行维度推广，即对表面和入射方向进行 4D 积分：

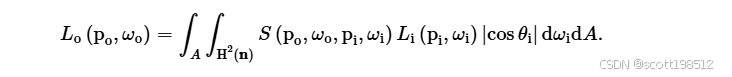
然而，使用 BSSRDF 渲染材质可以产生一些令人惊叹的效果，如下图所示，但代价是渲染方程的过于复杂。

图 7. 电影中的地下散射（PBS 新闻一小时）

4.反射类型

在开始之前，为了比较最终的视觉效果，我们可以将反射类型分为以下 4 大类：理想镜面反射、非理想（光泽）镜面反射、漫反射、回射。大多数真实表面都表现出这四种行为的混合。

理想镜面反射
- 将入射光散射到单一出射方向；
- 遵循反射定律；
- 例如镜子、玻璃；
漫反射（Lambertian）
- 入射光线以多个角度反射，而不仅仅是一个角度；
- 理想的漫反射表面，即向各个方向均匀散射光线，在现实世界中并不存在；
- 遵循朗伯定律；
- 例如哑光；
非理想镜面反射
- 也称为光泽镜面，或简称为镜面
- 优先在一组反射方向上散射光，从而定向漫射并显示其他物体的模糊反射；
- 例如塑料、高光漆；
回射型
- 主要沿入射方向散射光
- 例如天鹅绒、地球的月亮

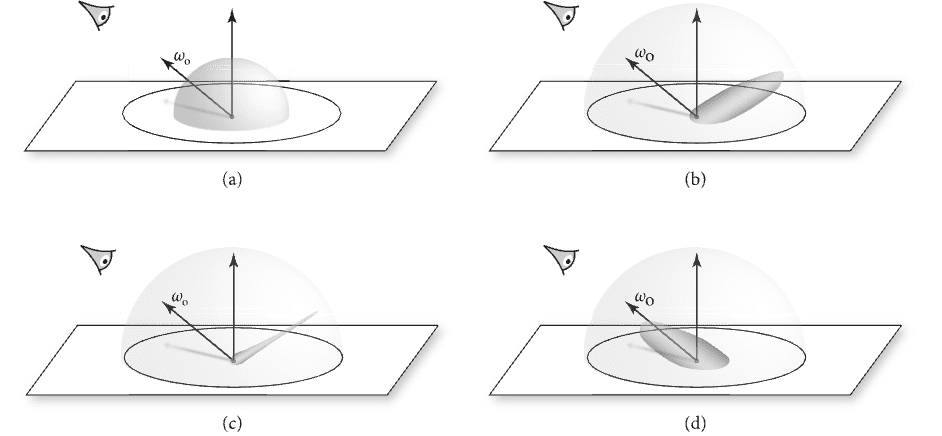
图 8.反射类型。（a）漫反射，（b）光泽镜面反射，

（c）近乎理想的镜面反射，（d）回射分布（参考资料3）

给定特定类别的反射，反射分布函数可能是各向同性的或各向异性的。

各向同性材料
- 选择表面上的一点并绕该点的法线轴旋转，则该点反射的光的分布不会改变；
- $f_r ((\theta_{\mathrm{i}}, \phi_{\mathrm{i}}) \to (\theta_{\mathrm{r}}, \phi_{\mathrm{r}}))$ 可以简化为具有 3 个参数的函数 $f_r (\theta_{\mathrm{i}}, \theta_{\mathrm{r}}, \phi_{\mathrm{i}} - \phi_{\mathrm{r}})$
各向异性材料
- 当你绕给定点的法线轴旋转它们时，会反射不同量的光；
- 例如头发、布料等。

5.材料类别

光由电磁波组成，因此物质的光学特性与其电学特性之间存在密切的相关性。材料通常分为三个主要光学类别：金属（或导体）、电介质（或绝缘体；虽然它们并不完全是同义词，但在图形中它们经常互换使用）和半导体。然而，鉴于可见物体表面很少表现出半导体特性，出于实用考虑，我们可以采用简化的分组，分为金属和非金属。

1）电介质
所谓电介质，就是不导电的材料（通常为非金属）。它们具有实值折射率并透射一部分入射光。典型的材料有：塑料、石头、木材、皮革、玻璃、水、空气。

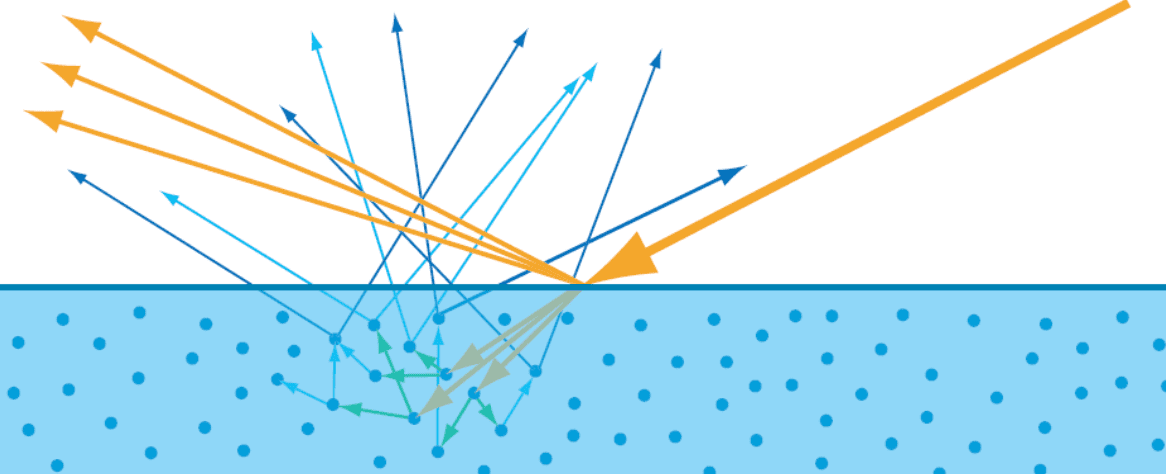
图 9.非金属 ( 参考资料5 )

2）导体

在导体中，价电子可以在原子晶格内自由移动，从而允许电流从一个地方流向另一个地方。当导体受到电磁辐射（如可见光）时，这种基本原子特性会转化为截然不同的行为：材料呈现不透明状态，并反射大部分入射光。这些材料具有吸收所有折射光的独特特性。
虽然一小部分入射光也会穿透导体内部，但它会被迅速吸收，并且完全吸收通常发生在顶部0.1纳米0.1纳米材料的折射率。因此，只有非常薄的金属膜才能传输相当数量的光。与电介质相比，导体理论上具有复值折射率 $\bar{\eta} = \eta + k \mathrm{i}$ ，典型导体如金属材料。

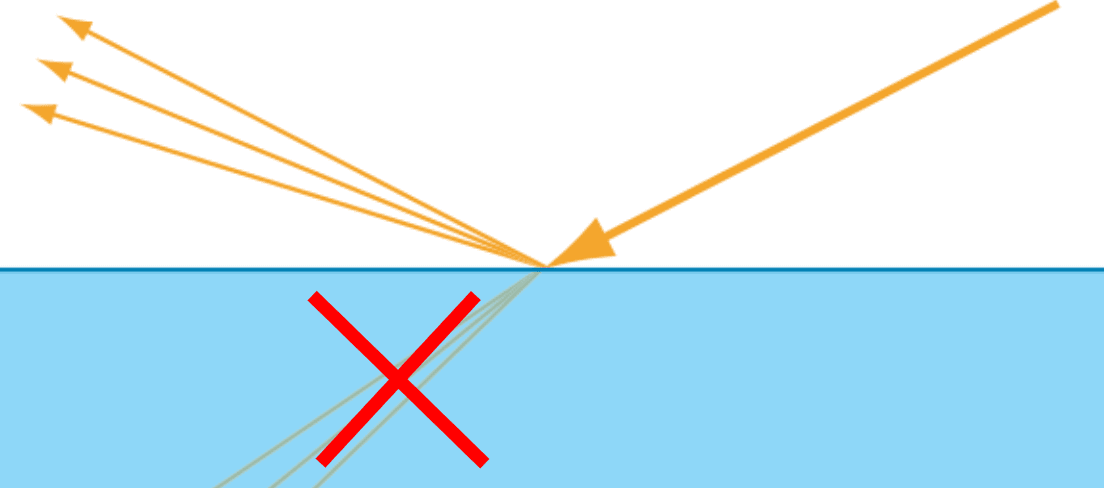
图 10.金属（参考资料5）

电介质、导体和半导体都遵循下一节介绍的菲涅尔方程（Fresnel equations）的规律。

6.基本反射和折射

6.1 理想漫反射

理想的漫反射表面会将入射光均匀地散射到各个方向。（虽然这种反射模型在物理上不太合理，但它可以合理地近似许多现实世界的表面，例如哑光漆。）从数学上讲，这意味着：

$f_r (\omega_{\mathrm{i}}, \omega_{\mathrm{r}}) = \frac{\rho}{\pi}$

其中， $\rho$ 是反射率，是出射辐照度与入射辐照度之间的比值。具体推导如下：

$\begin{aligned} L_\mathrm{o} & = \int_{H^2} f_r (\omega_{\mathrm{i}}, \omega_{\mathrm{r}}) L_{\mathrm{i}} (\omega_{\mathrm{i}}) \cos \theta_{\mathrm{i}} \; d \omega_{\mathrm{i}} \\ & = \frac{\rho}{\pi} \int_{H^2} L_{\mathrm{i}} (\omega_{\mathrm{i}}) \cos \theta_{\mathrm{i}} \; d \omega_{\mathrm{i}} = \frac{\rho}{\pi} E_{\mathrm{i}} \\ E_\mathrm{o} & = \int_{H^2} L_{\mathrm{o}} \cos \theta \; \mathrm{d}\omega = \frac{\rho}{\pi} E_{\mathrm{i}} \int_{H^2} \cos \theta \; \mathrm{d}\omega = \rho E_{\mathrm{i}} \end{aligned} \\ \\ \\\therefore \rho = \frac{E_{\mathrm{o}}}{E_{\mathrm{i}}} \leq 1$

6.2 理想的镜面反射和折射

理想的镜面只会沿单一方向反射或折射光线，这是由反射定律和斯涅尔定律的原理决定的。菲涅尔方程描述了从表面反射的入射光的比例；从而提供了反射或透射的入射光的比例。

图 11.使用理想镜面反射和折射渲染的龙模型（参考资料3）

6.2.1 反射

在理想的镜面反射中，入射光只是沿着法线反射。给定入射光的方向 $\omega_{\mathrm{i}} = (\theta_{\mathrm{i}}, \phi_{\mathrm{i}})$ ，根据反射定律，由此产生对应的出射方向 $\omega_{\mathrm{r}} = (\theta_{\mathrm{r}}, \phi_{\mathrm{r}})$ 的出射光。

反射定律

给定来自某个方向的入射光 $(\theta_{\mathrm{i}}, \phi_{\mathrm{i}})$ ，在与理想镜面相互作用后的单一反射方向为： $(\theta_{\mathrm{r}}, \phi_{\mathrm{r}})$ ，可以简单地表示为：

$(\theta_{\mathrm{r}}, \phi_{\mathrm{r}}) = (\theta_{\mathrm{i}}, \phi_{\mathrm{i}} + \pi)$

其中，在接触点处的法向量为 $\mathbf n$ ，满足以下关系：

$\omega_{\mathrm{r}} = - \omega_{\mathrm{i}} + 2 (\omega_{\mathrm{i}} \cdot \mathbf{n}) \mathbf{n}.$

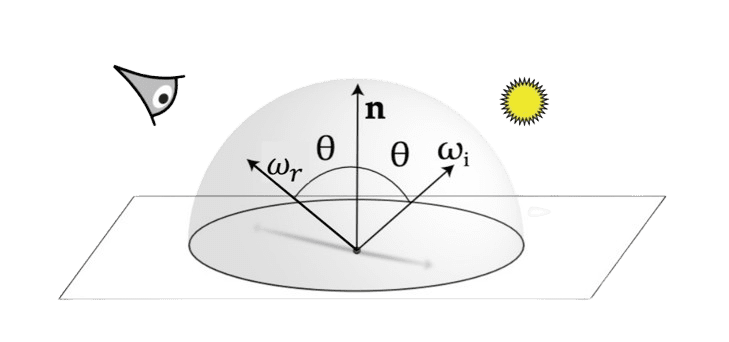
图12.反射定律

证明过程如下：

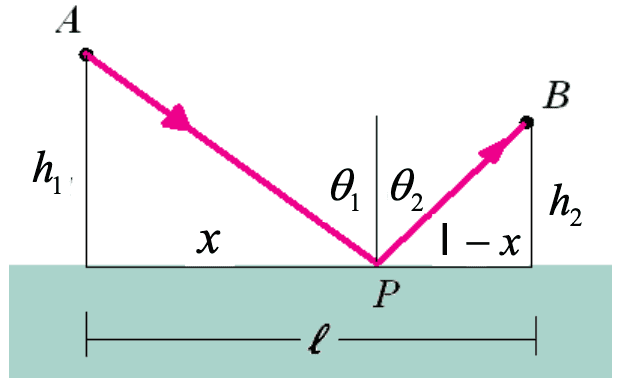
以下是基于费马原理对反射定律的推导过程，该方法参考自Giancoli等人2013年的工作：光线在两点之间传播时总是选择耗时最短的路径。

参考下图所示的光线路径。一束光线从点A出发，在表面点P处发生反射后到达点B，点B与点A的水平距离为ℓ。我们通过计算每条路径的长度，并将其除以光速，从而确定光线在两点之间传播所需的时间。最终可得：

$t = \frac{\sqrt{x^2 + h_1^2}}{c} + \frac{\sqrt{(\ell - x)^2 + h_2^2}}{c}$

取微分求最小值：

$0 = \frac{\mathrm{d}t}{\mathrm{d}x} = \frac{x}{c \sqrt{x^2 + h_1^2}} + \frac{- (\ell - x)}{c \sqrt{(\ell - x)^2 + h_2^2}}$

由此得到：

$sin(\theta_1)=sin(\theta_2)$

也就证明了反射定律。

基于这个结果，作用于表面上的方向向量 $w$ 可以分解为垂直和平行向量于接触点的法向量 $\mathbf n$ 的两个分量 $\omega_{\Vert} ,\omega_{\perp}$ ：

$\begin{aligned} \omega_{\Vert} & = \cos \theta \cdot \mathbf{n} = (\mathbf{n} \cdot \omega) \mathbf{n} \\ \omega_{\perp} & = \omega - \omega_{\Vert} = \omega - (\mathbf{n} \cdot \omega) \mathbf{n} \end{aligned}$

由此，得到对应于入射方向 $w_i$ 的出射方向 $w_o$ 为：

$\begin{aligned} \omega_{\mathrm{r}}=\omega_{\mathrm{r} \perp}+\omega_{\mathrm{r} \|} & =-\omega_{\mathrm{i} \perp}+\omega_{\mathrm{i} \|} \\ & =-\left(\omega_{\mathrm{i}}-\left(\mathbf{n} \cdot \omega_{\mathrm{i}}\right) \mathbf{n}\right)+\left(\mathbf{n} \cdot \omega_{\mathrm{i}}\right) \mathbf{n} \\ & =-\omega_{\mathrm{i}}+2\left(\mathbf{n} \cdot \omega_{\mathrm{i}}\right) \mathbf{n} . \end{aligned}$