多元线性回归

目录

多变量线性回归或多元线性回归

1.如何使用梯度下降法来处理多元线性回归

2.多元梯度下降法-特征缩放

3.多元梯度下降法-学习率

4.特征和多项式回归

---

多变量线性回归或多元线性回归

假设现在不仅有房屋大小，还有卧室的数量、楼层的数量、房子的年龄，那么现在就有了更多可以预测房屋价格的信息

有四个特征向量，用n表示特征向量的数目，因此n=4，依然用m表示样本的数量

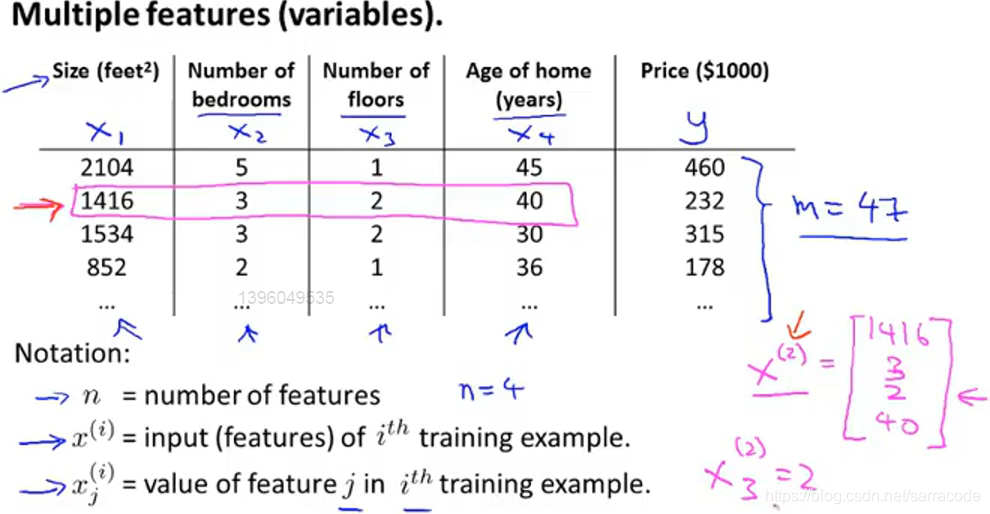
用表示第i个训练样本的输入特征值，因此对应表格中的第二行，在这里是一个四维向量

用表示第i个训练样本中第j个特征量的值

那么我们新的假设形式及化简方式如下图：

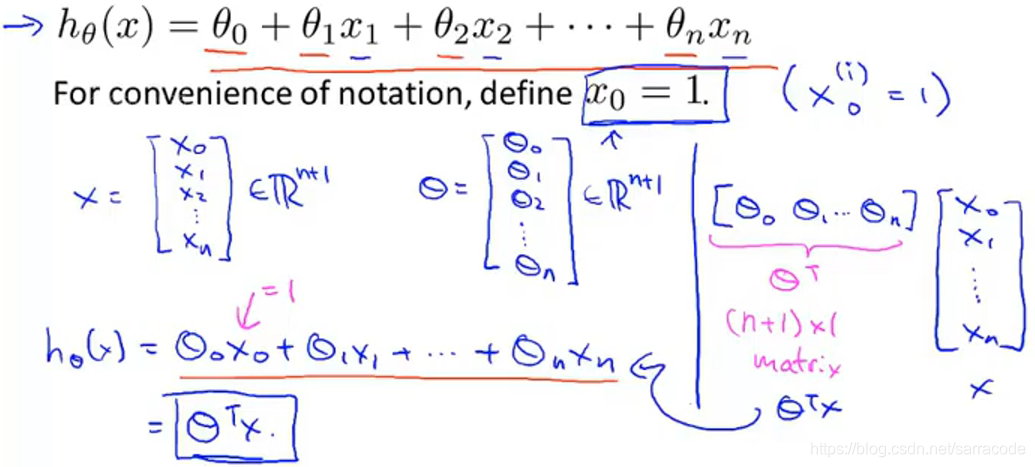
1.如何使用梯度下降法来处理多元线性回归

把n+1个参数看作成向量，即0，1，2，······，n

那么，接下来我们可以看到多元线性回归算法的公式如下：

2.多元梯度下降法-特征缩放

通常，我们执行特征缩放时，目的是将特征的取值约束到-1到+1的范围内

因为当1个特征值的取值范围远大于另一个时，可能会导致画出的代价函数的等高线图是一个又瘦又高的椭圆

那么，如果在这种等高线图上运行梯度下降的话，可能会需要很长一段时间，并且会来回波动，最终才收敛到全局最小值，情况如下：

因此，我们通过特征缩放会让他们的值的范围变得相近，那么这样梯度下降算法会更快的收敛

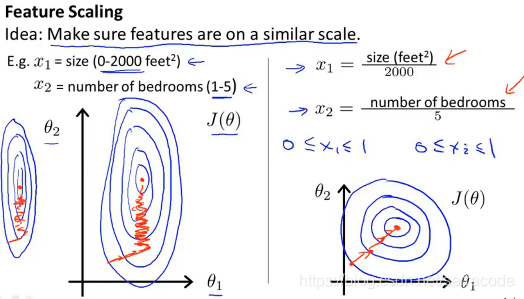
可以用如下式子来代替x1，其中1是训练集中特征x1的平均值，s1是该特征值的范围（最大值减去最小值或者设置为标准差也可以）

3.多元梯度下降法-学习率

下面图中的情况就是没有很好的收敛，那么可以让学习率a低一点

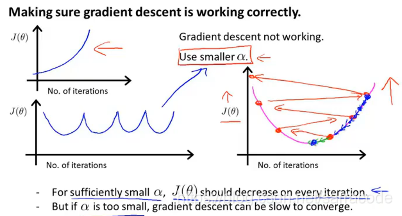
总结一下，如果学习率a太小，可能会收敛速度很慢；如果学习率a太大的话，代价函数J（）可能不会在每次迭代都下降，甚至可能不收敛

在调试过程中，通常会绘制J（）随迭代步数变化的曲线，可以帮助你弄清楚到底发生了什么，在这个过程中会尝试不同的a值

4.特征和多项式回归

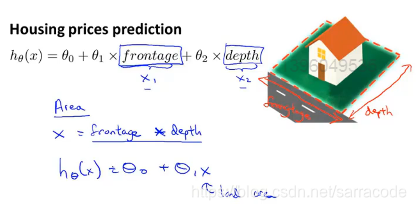
在这里虽然给了两个参数长和宽，但是我们可以通过定义新的特征值的方式来简化这个假设函数 ，那就是使用面积作为参数，那么就可以变为面积=长x宽

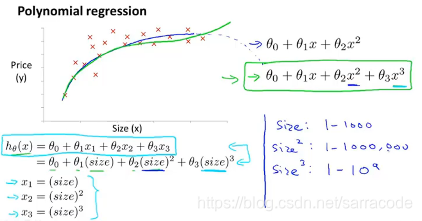
那么在这个例子中采用三次函数（下面左图）来拟合这个房屋价格的数据，因此在这里特征缩放就显得很重要

             

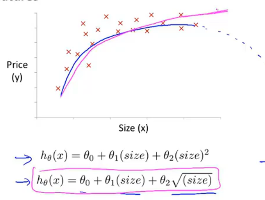
那我们还可以有其他的方式（上面右图）处理上面的例子，那么需要对一些函数和数据形状了解，才能得出更好的模型