蓝桥杯官网练习题（矩形运算）

最新推荐文章于 2025-12-30 20:44:15 发布

原创最新推荐文章于 2025-12-30 20:44:15 发布 · 85 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #职场和发展

博客围绕蓝桥杯相关题目，要求根据用户输入的两个矩形坐标，计算并输出它们的交集和并集矩形。输入为两个矩形的对角点坐标，不保证顺序；输出为交集和并集信息，若交集不存在则特殊输出。运行有时间和内存限制。

题目描述

在编写图形界面软件的时候，经常会遇到处理两个矩形的关系。

如图 1 所示，矩形的交集指的是：两个矩形重叠区的矩形，当然也可能不存在（参看图 2 ）。两个矩形的并集指的是：能包含这两个矩形的最小矩形，它一定是存在的。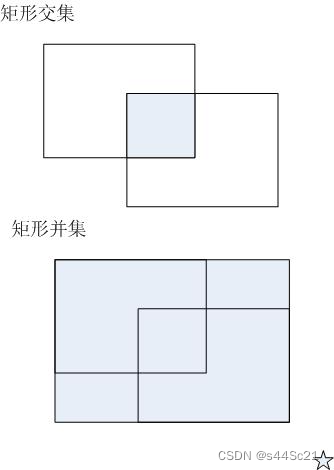

图 1

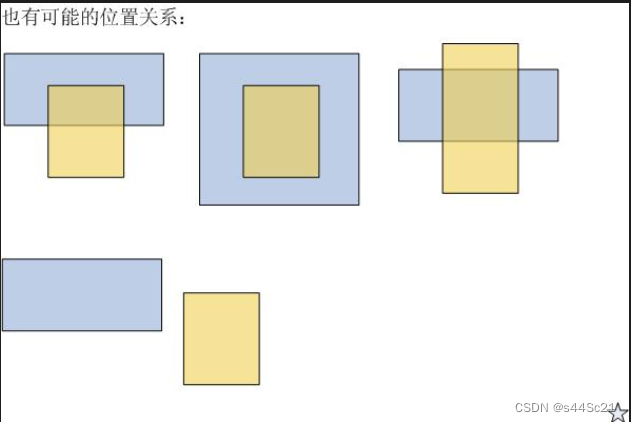
图 2

本题目的要求就是：由用户输入两个矩形的坐标，程序输出它们的交集和并集矩形。

矩形坐标的输入格式是输入两个对角点坐标，注意，不保证是哪个对角，也不保证顺序（你可以体会一下，在桌面上拖动鼠标拉矩形，4 个方向都可以的）。

输入描述

数据共两行，每行表示一个矩形。每行是两个点的坐标。

x 坐标在左，

y 坐标在右。坐标系统是：屏幕左上角为

(0,0)，

x 坐标水平向右增大；

y 坐标垂直向下增大。

输出描述

也是两行数据，分别表示交集和并集。如果交集不存在，则输出 NO。

前边两项是左上角的坐标。后边是矩形的长度和高度。

输入输出样例

示例

输入

100,220,300,100 
150,150,300,300

输出

150,150,150,70 
100,100,200,200

运行限制

import java.math.*;
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        String str=scan.nextLine();
        String[] str1=str.split(",");
        String str2=scan.nextLine();
        String[] str3=str2.split(",");

        //左上右下
        int x1=Math.min(Integer.parseInt(str1[0]),Integer.parseInt(str1[2]));
        int y1=Math.max(Integer.parseInt(str1[1]),Integer.parseInt(str1[3]));
        int x2=Math.max(Integer.parseInt(str1[0]),Integer.parseInt(str1[2]));
        int y2=Math.min(Integer.parseInt(str1[1]),Integer.parseInt(str1[3]));
        int x3=Math.min(Integer.parseInt(str3[0]),Integer.parseInt(str3[2]));
        int y3=Math.max(Integer.parseInt(str3[1]),Integer.parseInt(str3[3]));
        int x4=Math.max(Integer.parseInt(str3[0]),Integer.parseInt(str3[2]));
        int y4=Math.min(Integer.parseInt(str3[1]),Integer.parseInt(str3[3]));

        //交集(按左上右下找,得到左下右上坐标)
        int x5=Math.max(Math.min(x1,x2),Math.min(x3,x4));
        int y5=Math.max(Math.min(y1,y2),Math.min(y3,y4));
        int x6=Math.min(Math.max(x1,x2),Math.max(x3,x4));
        int y6=Math.min(Math.max(y1,y2),Math.max(y3,y4));

        //并集(按左上右下找,得到左下右上坐标)
        int x7=Math.min(Math.min(x1,x2),Math.min(x3,x4));
        int y7=Math.min(Math.min(y1,y2),Math.min(y3,y4));
        int x8=Math.max(Math.max(x1,x2),Math.max(x3,x4));
        int y8=Math.max(Math.max(y1,y2),Math.max(y3,y4));

        if(x5<x6&&y5<y6) {
            int length1=x6-x5;
            int hight1=y6-y5;
            System.out.printf(x5 + "," + y5 + "," + length1 + "," + hight1 + "\n");
        }
        else{
            System.out.println("NO");
        }
        int length2=x8-x7;
        int hight2=y8-y7;
        System.out.printf(x7+","+y7+","+ length2 +","+ hight2 +"\n");
        scan.close();
    }
}