计算机的本质是什么？逻辑？数学？

最新推荐文章于 2023-06-24 09:12:16 发布

原创最新推荐文章于 2023-06-24 09:12:16 发布 · 1w 阅读

17 ·

CC 4.0 BY-SA版权

本文介绍了计算机的发展历程，从ENIAC的诞生到图灵机理论，探讨了逻辑、代数和数学在计算机科学中的融合。讲述了亚里士多德的逻辑学、笛卡尔的解析几何、布尔的逻辑代数以及香农如何将二进制逻辑应用于计算机，阐述了计算机的本质是逻辑与数学的结合。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

计算机的诞生

1946年，在美国的宾夕法尼亚大学诞生了第一台现代电子计算机ENIAC。虽然在今天看来ENIAC计算能力连手机，甚至是十几块钱的计算器都比不上，但它在当时却是相当强大。ENIAC的体积非常庞大，得好几个大房间才能放下它，耗电也相当恐怖，一开机全城家家户户电灯都要变暗。

之所以称ENIAC是第一台现代计算机，是因为现代计算机理论的奠基人是图灵和冯诺依曼。这两个超级天才应该大家都听过，图灵提出了图灵机理论模型，而冯诺依曼设计确定了现代计算机的基础结构，他以数学语言阐述了计算机模型，将程序和数据都存在存储器中。

思想转为代码

实际上，计算机的发展并非一蹴而就。现代电子计算机属于狭义上的计算机，而广义上的计算机其实包括所有人类制造出来的计算设备，比如古代的算盘也属于计算机，只不过它是靠人力驱动的，再比如机械式计算机，使用机械齿轮来进行运算。

在广义上，对于计算机我们更应该将其理解为一种思想。计算机其实是为了帮助人类将思想转化为代码仿真出来，这就要求我们需要先对思想进行解码工作。而在古代就已经有先贤在逻辑学和数学方面进行研究，其中最伟大的思想家就是柏拉图和亚里士多德，他们俩也互为师生关系。

亚里士多德首次将哲学与科学分离，并在逻辑方面进行了研究，他认为逻辑是一切科学的基础，是形式逻辑学的创始人奠基人。他将人的思维和存在联系起来，然后根据实际阐明逻辑。亚里士多德在推理逻辑中提出了三段论：

所有动物都会死
所有人都是動物
所以，所有人都會死

异类联想

自亚里士多德以来，逻辑学和数学都是分开研究各自发展的。直到后来德国的莱布尼茨哲学家才尝试将它们结合起来，通过将两种现有的思想结合起来，以形成第三种创新思想，即异类联想。后来发展出数理逻辑这门学科，以数理逻辑思想为基础的计算科学也在不断地发展着。对于这些人，他们的目标是将抽象的逻辑用精确的数学符号来表示，

对于计算机，多数人会认为计算与逻辑是密不可分的，甚至还有人认为计算的本质其实就是逻辑。而逻辑与数学的关系是，逻辑并不等于数学，只是曾经有人想以逻辑为基础来构建数学。逻辑、计算和数学三者应该如何融合？

调和代数与几何

在笛卡尔之前，代数和几何各自为政，它们是两个独立不同的学科。然而几何过度依赖图形与形式，代数又过分受公式限制，这都制约了它们的发展。这时法国数学家笛卡尔则通过异类联想将这两者联系了起来，创立了解析几何，从而他也被称为解析几何之父。

笛卡尔发明了现在大家很熟悉的直角坐标系，x轴和y轴，通过坐标系成功调和了几何与代数。从此一个圆可以用方程来描述，也可以用坐标系画图来表示。此外，解析几何也为微积分的创立奠定了基础。

逻辑与代数的融合

现在估计多数人都没听过布尔，程序员最多也是知道布尔类型，但其实可以说布尔逻辑是计算机的核心理论。莱布尼茨一直的梦想就是将逻辑学和数学进行融合，而英国的数学家乔治布尔则通过异类联想将亚里士多德的三段论与代数结合起来，并发明了二进制，将这个梦想向前推动。

算术可来实现加法乘法，而逻辑主要是或、与等，能否将它们结合起来呢？逻辑或类似于加法，即两个相交集合中，有些元素只属于其中一个集合。逻辑与则是两个相交集合共同拥有的那些元素，这部分类似于乘法。而且是只有在0和1的情况下才能成立，这就将算术与逻辑通过二进制运算连接了起来。

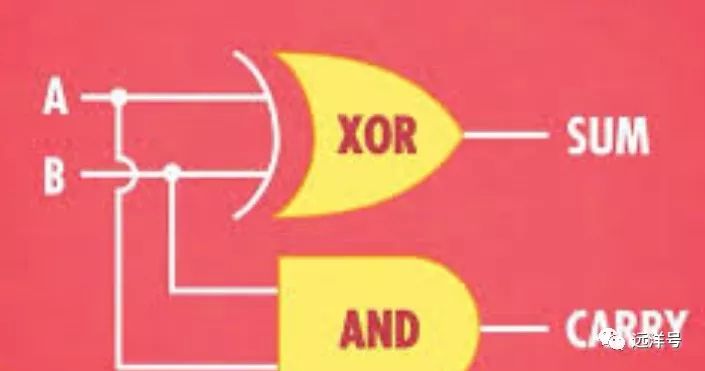
香农的二进制

正是克劳德香农将布尔的逻辑运算带入计算机，香农是一名贝尔实验室的工程师。比起有名的科学家，香农的名气不算大，估计只有计算机专业的人有了解过他，而且大家知道他估计也是因为信息论。其实香农的伟大成就还包括他将逻辑融入到计算机内，从而成功将逻辑层和物理层进行分离。得益于香农将逻辑映射到现实物理世界，至此计算机得到了空前的发展。

其实是他将二进制运算与电子器件相结合，实现了逻辑功能，奠定了如今计算机的运算机制。他设计出了相加电路来构造复杂的算术运算，这些电路也成为现代计算机的组件。纵使后面越做越小越来越先进的晶体管，也是基于香农的电路原理。

图灵的图灵机

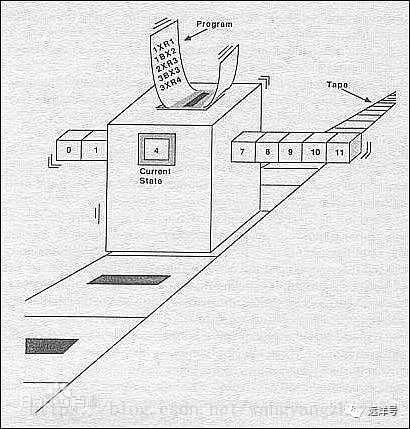
图灵机即图灵计算机，是由数学家艾伦·麦席森·图灵（1912～1954）提出的一种抽象计算模型。图灵尝试以数理逻辑语言来设计计算机，将人们使用纸笔进行数学运算的过程进行抽象，由一个虚拟的机器替代人们进行数学运算。

图灵机有一条无限长的纸带，纸带分成了一个一个的小方格，每个方格有不同的颜色。一个机器头在纸带上进行移动，机器头有一组内部状态，还有一些固定的程序。在每个时刻，机器头都要从当前纸带上读入一个方格信息，然后结合自己的内部状态查找程序表，根据程序输出信息到纸带方格上，并转换自己的内部状态，然后进行移动。

每一个会决策、会思考的人都可以被抽象地看成一台图灵机，该模型主要有四要素：输入集合、输出集合、内部状态和固定的程序。如果把人进行抽象，那么输入集合就是所处环境中所看到、听到、闻到、感觉到的一切；输出集合就是人的每一言每一行，还有表情动作；内部状态集合则可以把神经细胞的状态组合看成一个内部状态，所有可能的状态集合将是天文数字。