LeetCode hot 100—腐烂的橘子

rigidwill666

于 2025-04-15 20:19:05 发布

阅读量687

点赞数 29

CC 4.0 BY-SA版权

分类专栏： leetcode 文章标签： leetcode 算法职场和发展 bfs c++ 数据结构

本文链接：https://blog.youkuaiyun.com/rigidwill/article/details/147257207

leetcode 专栏收录该内容

87 篇文章

订阅专栏

题目

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例

示例 1：

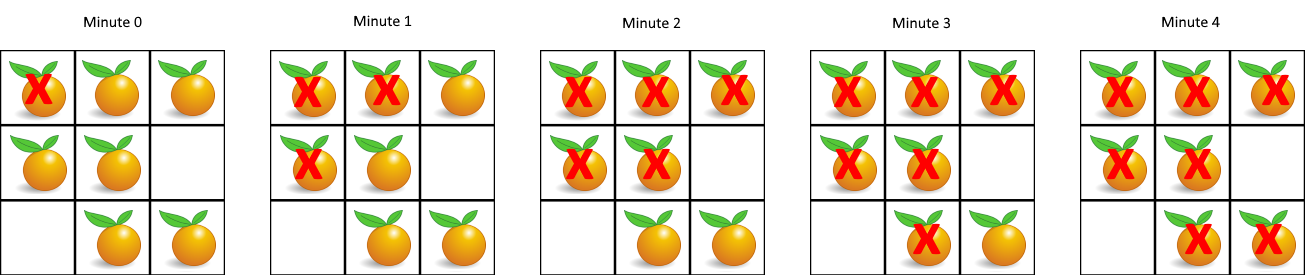
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

分析

为了解决这个问题，可以使用广度优先搜索（BFS）算法。BFS 非常适合解决这类逐层扩散的问题，因为它能够按照层次顺序遍历图，恰好符合橘子腐烂的过程，即每分钟向周围扩散一层。

BFS

代码解释

初始化部分：遍历网格，将所有腐烂的橘子的坐标加入队列 rottenQueue，同时统计新鲜橘子的数量 freshCount。

BFS 过程：

当队列不为空且还有新鲜橘子时，进行 BFS。
每一轮 BFS 处理当前队列中的所有腐烂橘子，将其周围的新鲜橘子变为腐烂橘子，并将新腐烂的橘子加入队列。
每一轮 BFS 结束，分钟数 minutes 加 1。

结果判断：如果最后没有新鲜橘子了，返回 minutes；否则返回 -1。

时间复杂度：O( $m\times n$ )

空间复杂度：O( $m\times n$ )

class Solution {
public:
    int orangesRotting(std::vector<std::vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        std::queue<std::pair<int, int>> rottenQueue;
        int freshCount = 0;
        int minutes = 0;

        // 初始化队列，将所有腐烂的橘子加入队列，并统计新鲜橘子的数量
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 2) {
                    rottenQueue.push({i, j});
                } else if (grid[i][j] == 1) {
                    ++freshCount;
                }
            }
        }
        // 定义四个方向：上、下、左、右
        std::vector<std::pair<int, int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        // BFS 过程
        while (!rottenQueue.empty() && freshCount > 0) {
            int currentSize = rottenQueue.size();
            for (int i = 0; i < currentSize; ++i) {
                auto [x, y] = rottenQueue.front();
                rottenQueue.pop();
                // 遍历四个方向
                for (const auto& [dx, dy] : directions) {
                    int newX = x + dx;
                    int newY = y + dy;
                    // 检查新位置是否合法且为新鲜橘子
                    if (newX >= 0 && newX < m && newY >= 0 && newY < n && grid[newX][newY] == 1) {
                        grid[newX][newY] = 2;
                        --freshCount;
                        rottenQueue.push({newX, newY});
                    }
                }
            }
            // 每一轮 BFS 结束，分钟数加 1
            ++minutes;
        }
        // 如果还有新鲜橘子，说明无法全部腐烂，返回 -1
        return freshCount == 0 ? minutes : -1;
    }
};