TensorFlow训练神经网络
在之前的记录8中我们学习到了如何在神经网络上进行推理,而本次的记录9我们将目光集中在神经网络的训练中
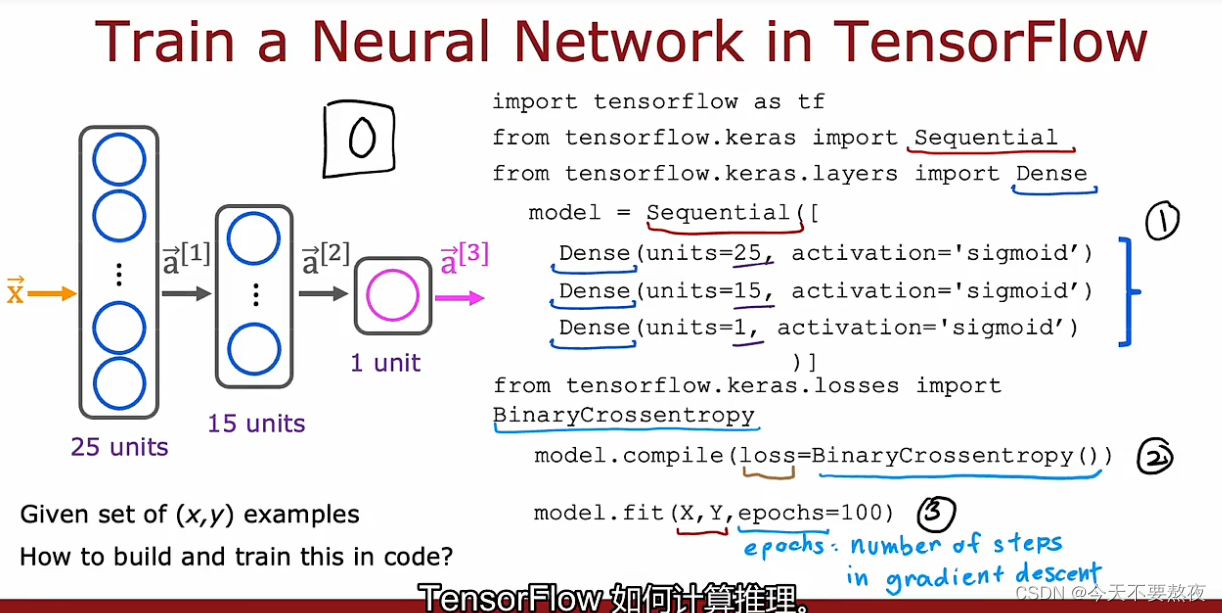
Step1是指定模型,此模型告诉TensorFlow如何去在神经网络上计算推理
Step2是使用特定的loss or cost function去编译compile模型
Step3是训练模型
要求TensorFlow编译模型的关键步骤是指明specify你要使用的损失函数或者成本函数loss function/cost function,这里我们采用的损失函数是二元交叉熵损失函数
fit函数告诉TensorFlow在数据集X,Y上,去拟合你在步骤1提出的那个模型,使用你在步骤2中提出的loss or cost function,对于epoch来说是表示梯度下降的步数
用于训练神经网络的TensorFlow代码实际在做什么
同样我们也要搞明白这些代码实际在干什么,方便我们在debug时进行更有效率的调整
这里我们与逻辑回归模型的训练作为类比,简要列出对应的神经网络如何进行训练

loss function是在一个训练样本上,cost function是在整个训练集上求损失函数的平均值
Step1构造模型
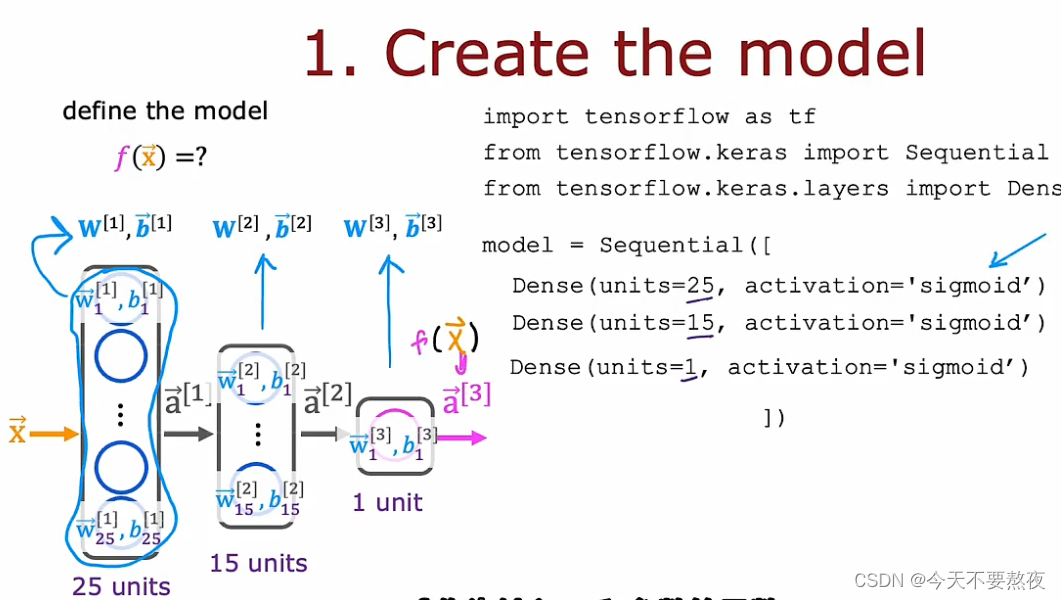
这个代码片段指定了整个神经网络的架构
Step2指明损失函数和成本函数
在这一步中我们需要指定损失函数进而也指定了成本函数,最后的输出可以是f(x)也可以为强调此输出和所有参数有关系,写成f W,B(x)

在mnist数字识别问题中识别是0还是1,即二分类问题,我们使用二元交叉熵损失函数(此函数和在逻辑回归中使用的loss function一样),其中binary是为强调我们在进行的是二分类问题
如果是回归问题,我们想要使用不同的损失函数编译我们的模型,所以可以使用均方误差
Step3要求TensorFlow去最小化成本函数
利用上述公式进行前面所设定的100次梯度下降,而为了实现梯度下降我们所需要的关键一步是计算这些偏导数项,这里我们会用到反向传播算法,TensorFlow可以为我们完成所有的这些事情,我们所要做的就是调用这个model.fit函数,指定所使用的数据集和所要进行的迭代次数
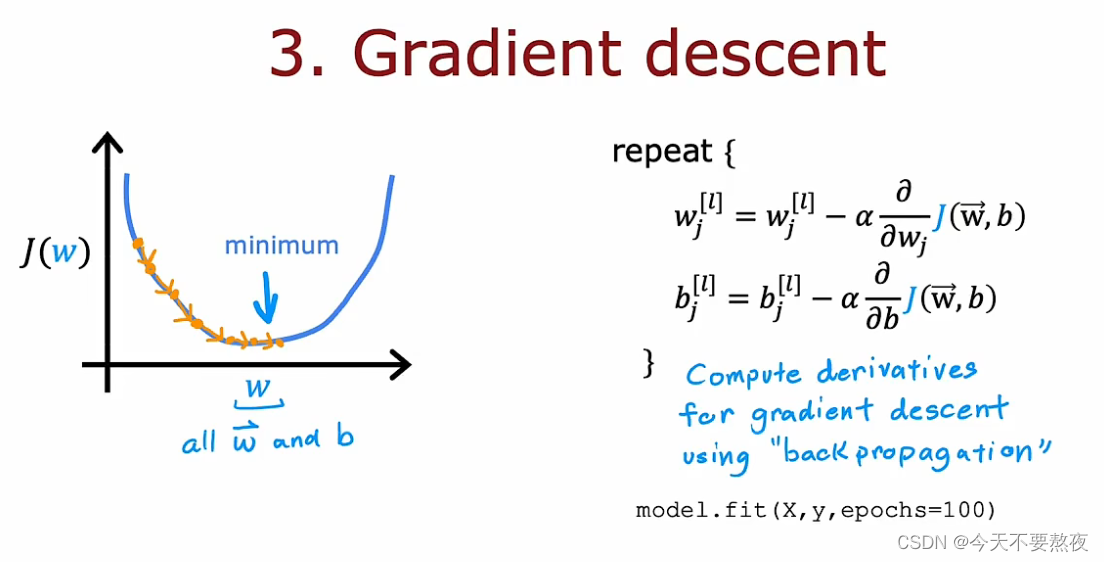
其实TensorFlow使用了一个要比梯度下降快一点的算法,我们会在之后的课程里学习到
我们学会了如何去训练一个神经网络或者有时候也称之为多层感知器,这时候可以对神经网络进行一些修改,得到更好性能的神经网络
修改激活函数
这三个可能是迄今为止使用最多的激活函数,之后我们还会学到softmax激活函数用于多分类问题
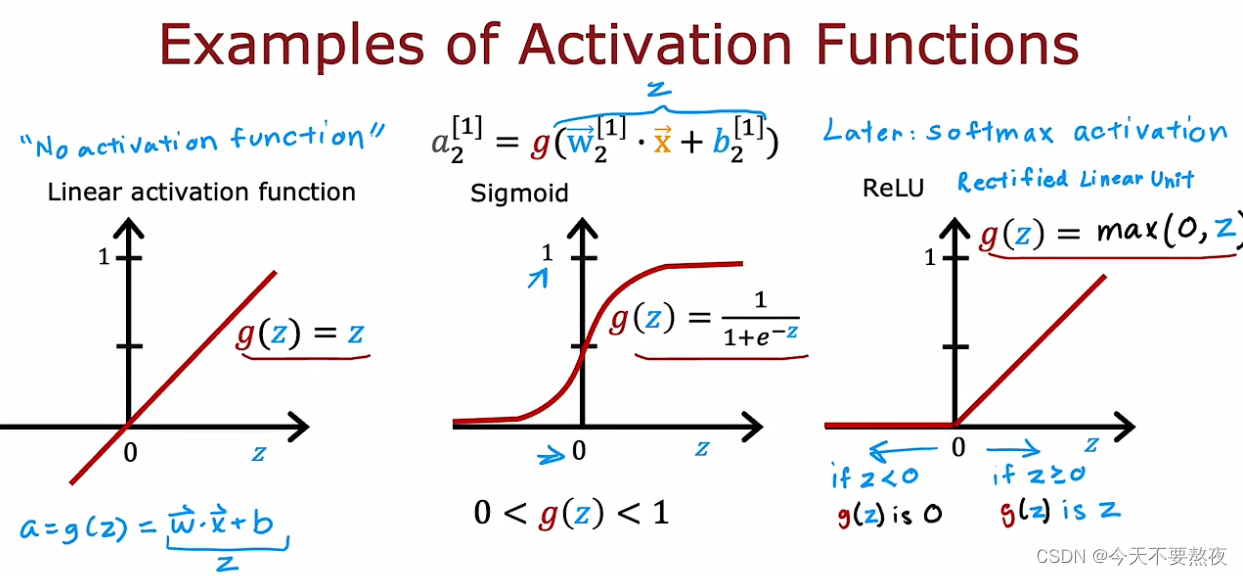
如果你使用的是这里的线性激活函数,我们会说其实你没有使用激活函数,因为最后就没有g的参与,通过这些激活函数我们可以构建丰富多样的强大的神经网络
如何选择激活函数
我们可以为神经网络中的不同神经元选择不同的激活函数
输出层
取决于目标标签或者是说真实标签是什么,输出层的激活函数的选择也有不同:二分类问题我们通常会使用sigmod函数,如果标签y可正可负可以使用线性激活函数,如果y取非负值那么可以使用Relu函数
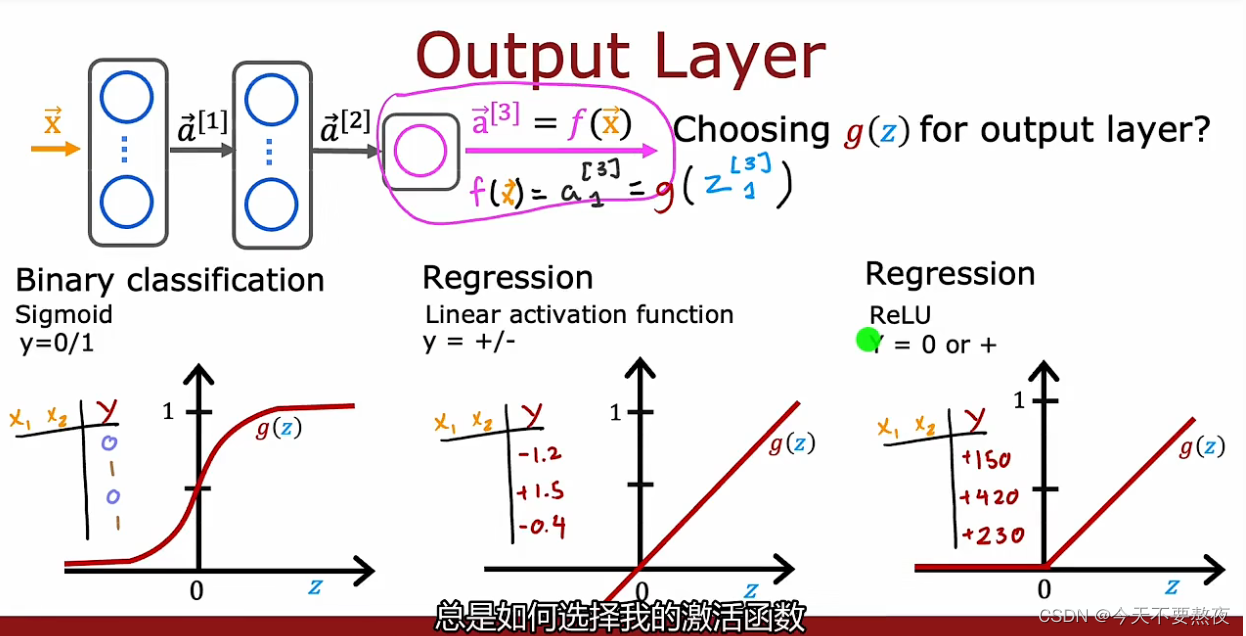
隐藏层
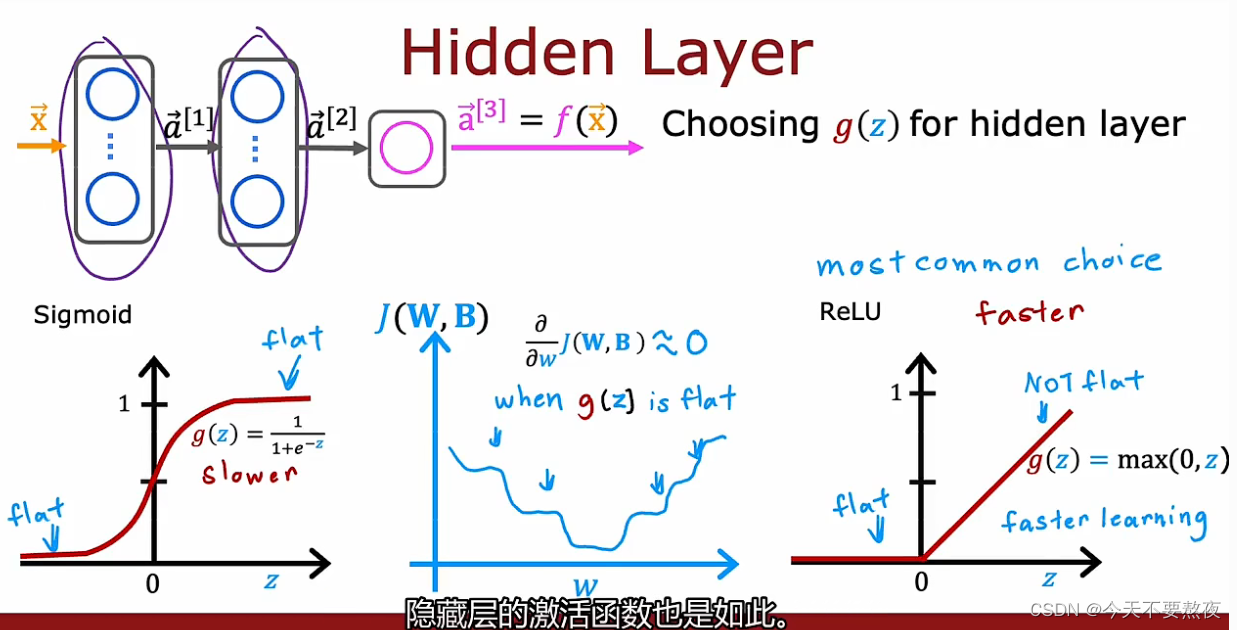
虽然梯度下降优化的是成本函数,但是激活函数是进行计算的一部分(one piece of what goes into computing ),所以对于成本函数的图像,Sigmod函数由于自身在左右两侧都会有flat的地方,所以使得也会出现很多平坦flat的地方,由于梯度很小所以学习的速度很慢,因此Relu函数要比Sigmod函数学习的速度更快,另一方面也因为Relu函数的表达式相比于Sigmod函数而言更简单,所以Relu激活函数几乎是神经网络中最常用的激活函数,几乎很少使用Sigmod函数除非是在二分类问题中
所以在隐藏层中默认采用Relu函数作为激活函数

输出层如果采用线性激活函数的话,语法表示为,activation='linear'
为什么模型需要激活函数
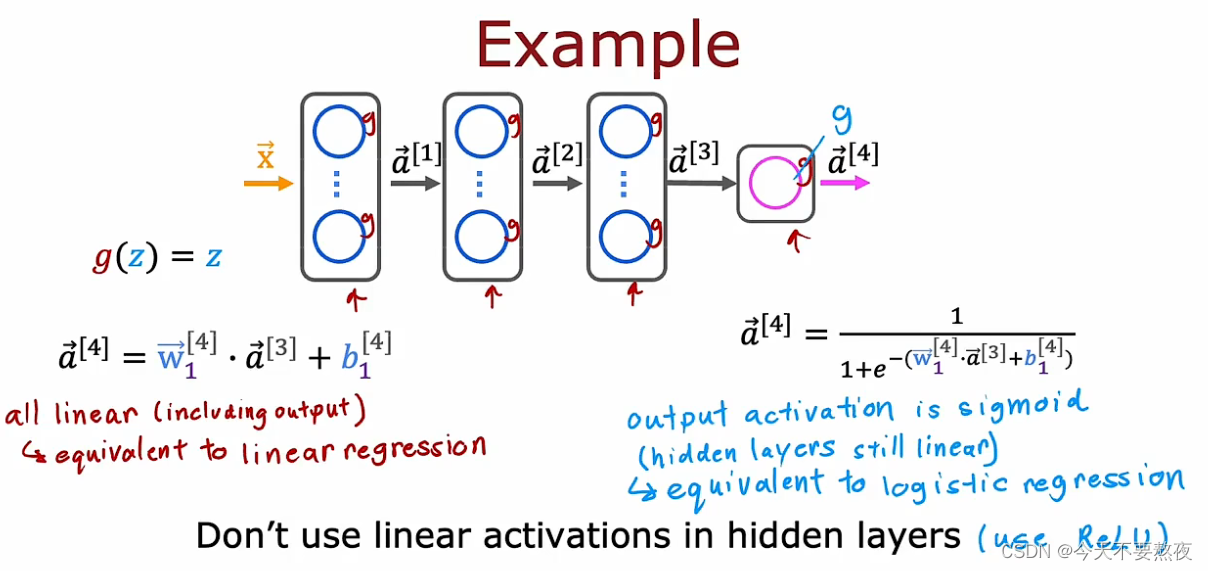
如果所有隐藏层都采用线性激活函数的话,那么如果输出层是线性激活函数,则就是线性回归模型,输出层是sigmod激活函数,则就是逻辑回归模型,相当于隐藏层没有作用
多分类问题构建神经网络
Softmax计算输出值
Softmax是在二分类问题中运用的逻辑回归的推广(泛化)

Softmax中的loss function
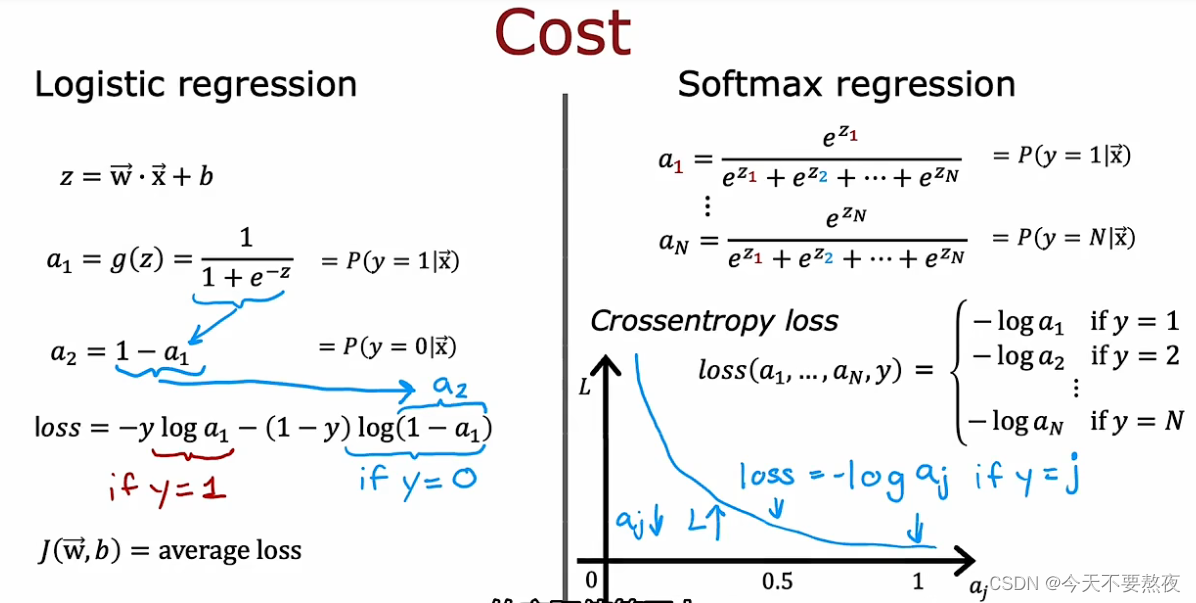
Softmax做输出层的神经网络
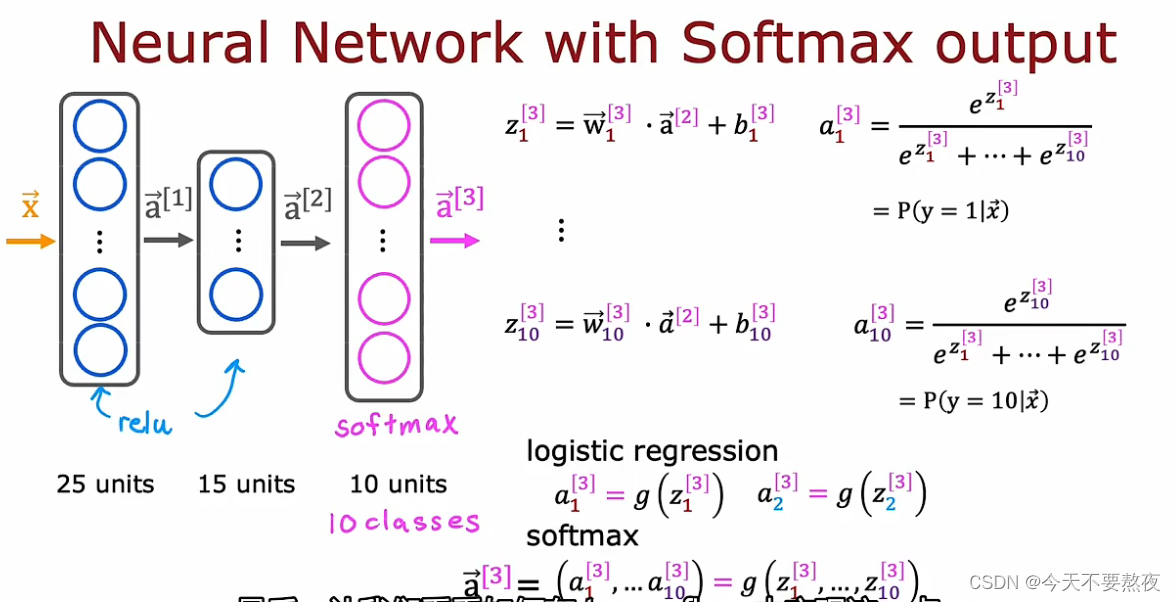
相比于logistic regression,a1就是z1的函数,a2就是z2的函数,Softmax呢a1是z1一直到zn的函数
TensorFlow代码实现Softmax
前面我们所提到的Softmax的损失函数称为SparseCategoricalCrossentropy稀疏分类交叉熵损失函数,而在逻辑回归中的损失函数称为BinaryCrossentropy二元交叉熵

这里的code可以奏效,但是不推荐使用,在之后的学习中我们会看到实施效果更好的一个版本





 本文详细介绍了如何在TensorFlow中训练神经网络,包括指定模型、设置损失函数、使用fit函数进行训练,以及讨论了激活函数的选择(如ReLU和Sigmoid),并提及了在多分类问题中使用Softmax的实例。
本文详细介绍了如何在TensorFlow中训练神经网络,包括指定模型、设置损失函数、使用fit函数进行训练,以及讨论了激活函数的选择(如ReLU和Sigmoid),并提及了在多分类问题中使用Softmax的实例。

















 471
471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








