机器学习----AndrewNg视频笔记记录03

梯度下降算法介绍

梯度下降算法可以被用作try to minimize任何函数而不仅仅是线性回归的成本函数，所以为了使得对梯度下降的讨论更加普遍，并且梯度下降也适用于更一般的函数，于是我们在此处使用w1到wn和b的参数，并在outline（概述）中表达出梯度下降的三个工作步骤

在线性回归中初始值是多少并不重要，常见的一个选择就是把w和b都设置为0

对于具有平方误差成本函数的线性回归，J的图像会总是以碗状bowl shape或者吊床形结束，但是J不总是呈现这种形状，于是最小值可能有多个：

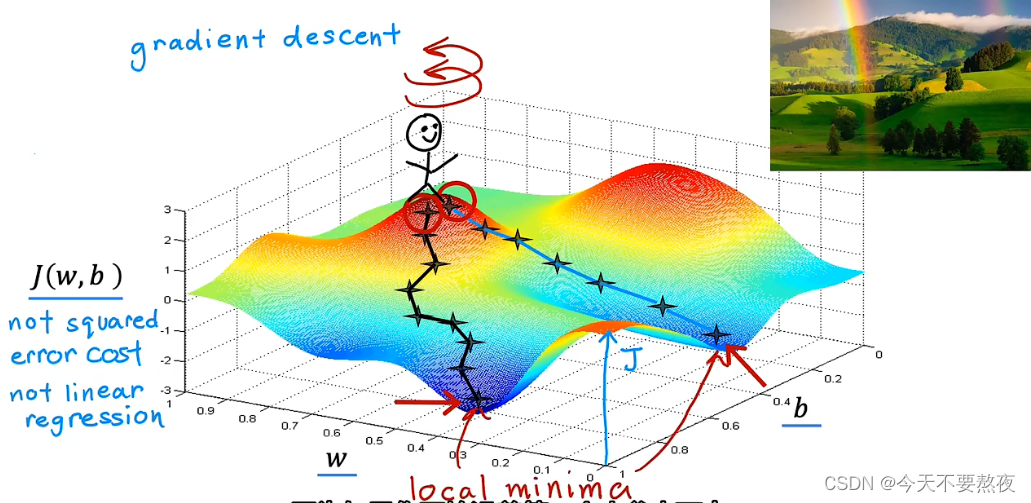
梯度下降所做的就是帮助你找最陡的下坡路线，其有一个有趣的特性就是：局部最小值

梯度下降的实现（数学表达式）

α学习率，在做的就是控制步长的大小；导数项（偏导）在做的就是控制朝着哪个方向迈步

要同时更新w和b这两个参数，不要使用右边这样的；并且重复这两个步骤直到收敛convergence

理解梯度下降（what it's doing和why it  might make sense）

为了简化问题，更加直观，这里我们仍然将b设置为0

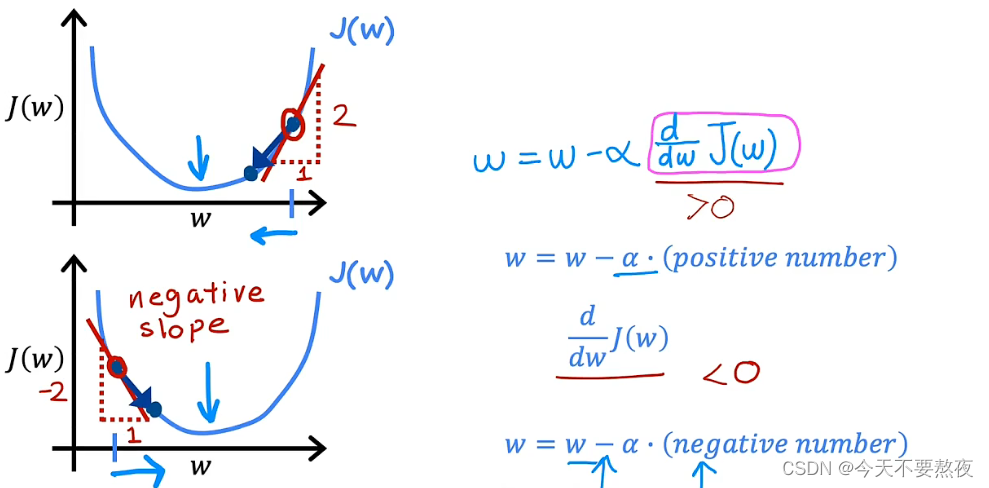
当你选择从右侧开始进行梯度下降时，通过计算其偏导数项为正值，它使得w越来越小，直至接近最小值；当你选择从左侧开始进行梯度下降时，通过计算其偏导数项为负值，它使得w越来越大，直至接近最小值

学习率的选择

如果学习率的值很小，梯度下降的速率可能会很慢，即使最终也可以达到最小值

如果学习率的值很大，梯度下降采用很大的步伐，可能会越过最小值点，不会收敛甚至发散

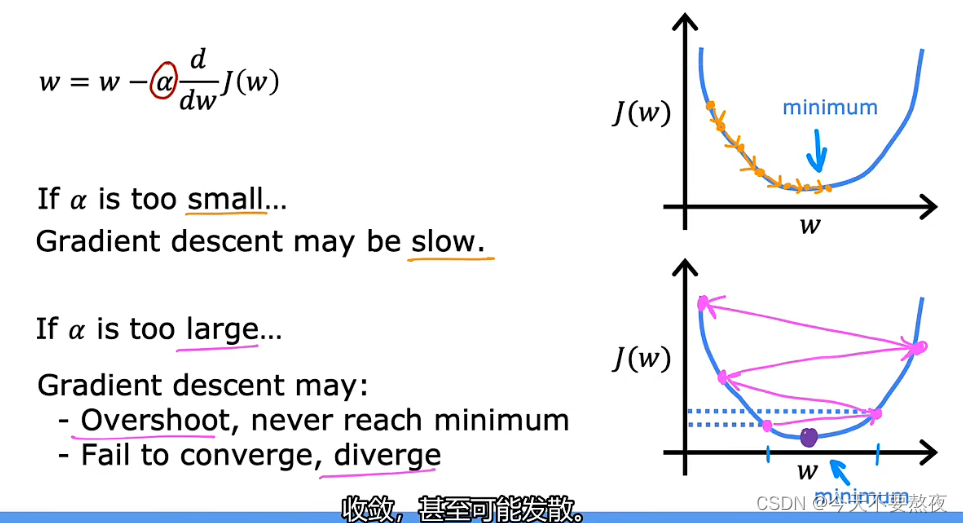
需要明确的一点是，当我们已经处在了最小值点，此时的导数项已经为0，所以参数会保持不变。

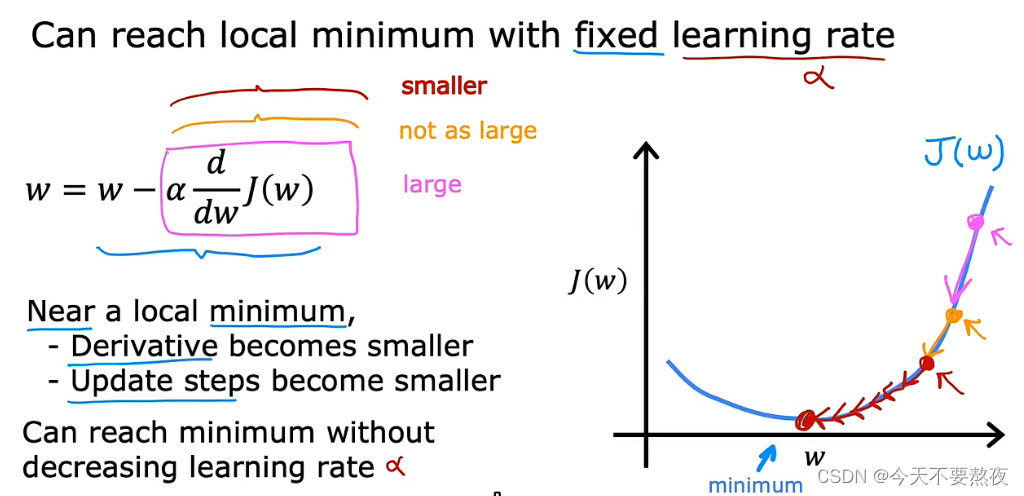
当靠近局部最小值点时，导数项会变得越来越小，导致更新的步伐也越来越慢，这一过程并不需要减少学习率便可以到达最小值 

线性回归算法

将此前的线性回归模型，成本函数和梯度下降算法pull together就得到我们机器学习的第一个学习算法：线性回归算法，此处成本函数我们依旧采用平方误差成本函数。于是，这就允许我们训练线性回归模型去拟合数据并形成一条直线。

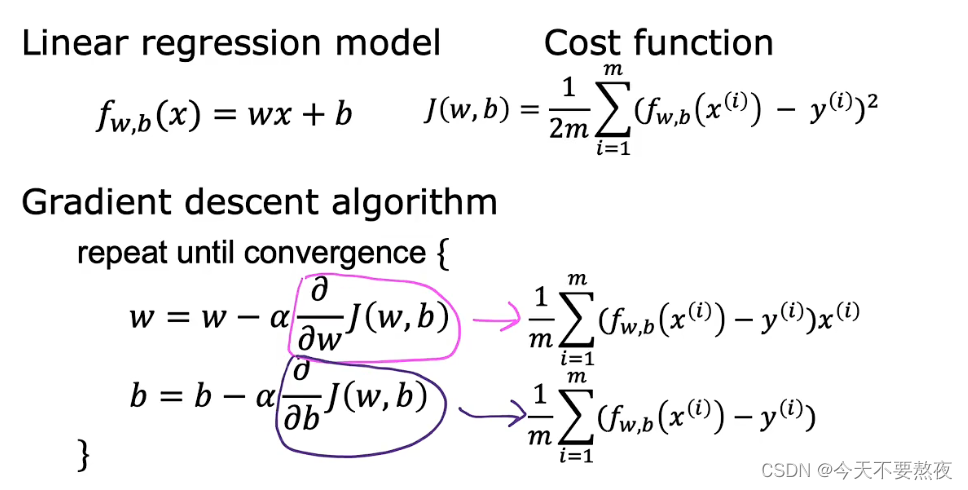
 关于这两个偏导数项是如何计算出的，Andrew给出了推导：就是一个简单的求导过程

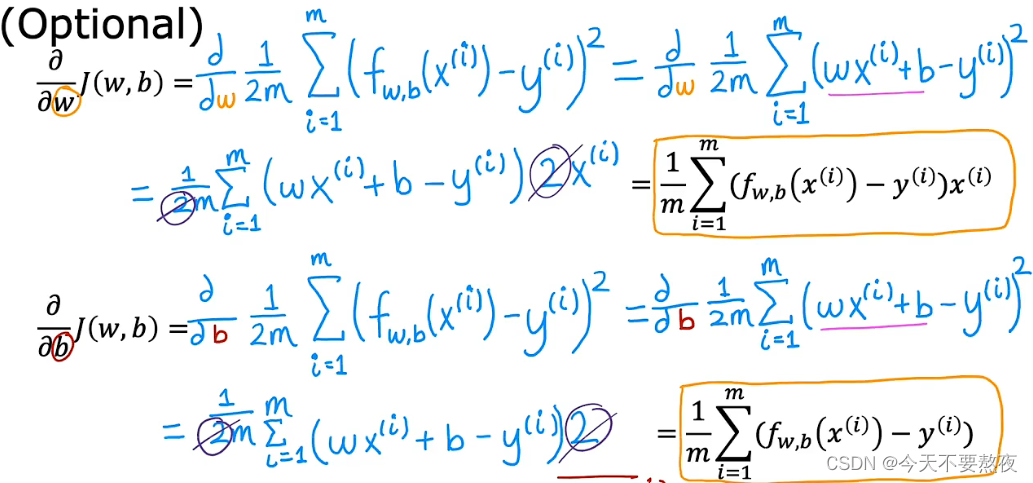
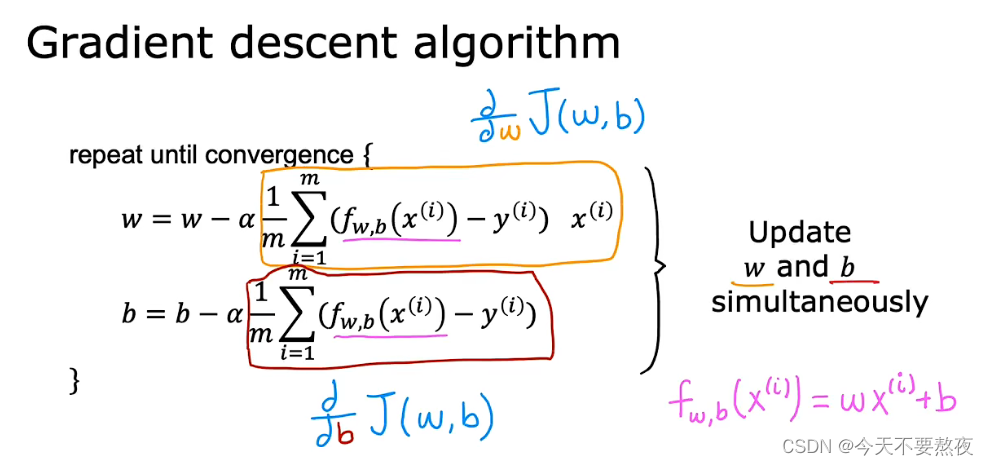
在计算出这两个导数项之后，梯度下降算法可以表达为：

当线性回归问题中使用平方误差成本函数时，成本函数不会有多个局部最小值，因为此函数为凸函数，informally来讲，图像是碗状的（bowl shape）只有单个全局最小值，而不会存在多个局部最小值。

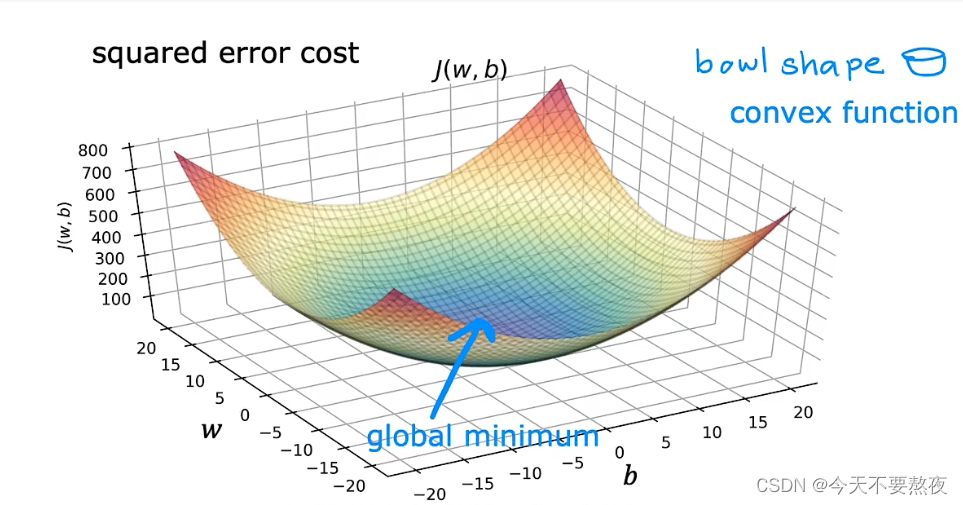
所以当我们在凸函数上使用梯度下降的时候，as long as我们采用了恰当的学习算法那么就会始终收敛到全局最小值

运行梯度下降（线性回归算法应用in action）

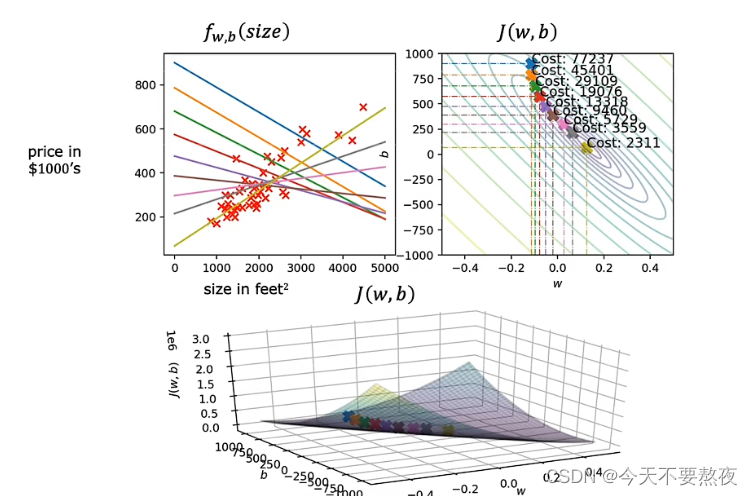
Andrew在本例中并不是初始化w和b都为0的情况，而是从这个浅蓝色这个点开始进行梯度下降，不断下坡，使得成本函数逐渐减少，最终达到全局最小值处。

更准确地讲，这种梯度下降方法称之为batch gradient descent

实际上梯度下降的类型有很多，而在线性回归问题中我们采用batch gradient descent

mini-batch梯度下降

在batch梯度下降中你必须处理完所有的训练样本（处理整个训练集），才可以进行一次梯度下降，然后需要再处理一次才能再进行一次梯度下降，而mini-batch则是将整个训练接分割成一个个的小样本集，instead of处理整个训练集，它只处理每一个分割出来的mini-batch.

当你有一个很large的训练集时采用mini-batch的效率要比batch的效率高，所以在训练巨大数据集的时候都会使用到mini-batch

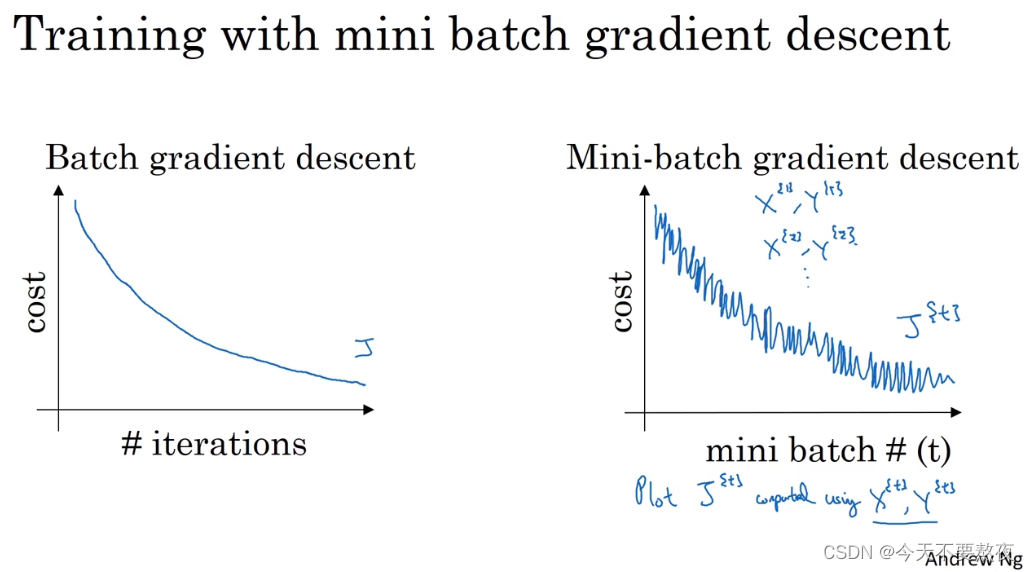
如果mini-batch的size为样本数量m，则退化为batch梯度下降，其弊端就是在训练集很大的情况下每一个迭代所需要的时间太长，如果训练集适中那么batch的效果不会很差

如果mini-batch的size为1，则变为随机梯度下降，每一个样本都是一个mini-batch，虽然总体上是朝着最小值方向但是噪声将会很大，这也失去了向量化的优势

而适当大小的mini-batch的size，学习得更快，其优势在于：利用了向量化的优势，另一方面你无需等待整个训练集被处理完就可以开始进行后续工作

它同样不会总朝着最小值靠近，但它比随机梯度下降要更加持续地靠近最小值的方向，它也不一定在很小的范围内收敛或波动如果出现这一问题，可以通过慢慢减少学习率（学习率衰减）的方式解决

此处当训练样本m为5,000,000时，每1000个样本归入一个mini-batch

x(i)是指第i个训练样本，z[l]是指神经网络中第l层的z值，X{t}和Y{t}是指不同的mini-batch

第一周结语

通过学习，我们知道了对于只有一个输入变量的时候如何实现线性回归，接下来我们将会引入多个输入特征，学习如何让它拟合非线性曲线，这些改进将会使得算法更加有意义和有价值