恶意数据注入检测综述

无线传感器网络中恶意数据注入的检测：综述

1. 引言

无线传感器网络（WSNs）由于其灵活性、低成本和易于部署，成为从物理空间收集数据的一个理想解决方案。无线传感器网络的应用涵盖共享环境和个人环境中的多种任务。在共享环境中，应用包括对基础设施（如供水网络）的监测、道路 traffic 的改善、环境参数的监控以及监视。在个人环境中，应用包括监测家庭的能源效率、用户活动（如锻炼和睡眠），以及通过可穿戴和植入式传感器对生理参数进行医疗保健监测。

在某些方面，无线传感器网络与传统的有线和无线网络相似，但在其他方面也存在差异，例如传感器的计算和电源资源有限。无论用于监测人体还是广阔的洪泛平原，传感器都需要成本低廉、体积小巧、支持无线通信，并具备低功耗特性，这正是其主要优势所在。但这些特性同时也带来了其主要局限性，因为它们会导致更频繁的失效、物理防护差、冗余和处理能力有限，以及执行复杂操作的能力受限。无线传感器面临更高的受损风险。它们的部署通常无人看管且物理上可访问，而使用防篡改硬件往往成本过高。无线通信介质难以保障安全，且协议栈的各层都可能被攻破。加密操作和密钥管理会消耗宝贵的计算和电源资源，且一旦节点被攻破，这些措施便无法提供有效防护。然而，尽管存在这些风险，无线传感器网络正越来越多地被用于监控关键基础设施和人类健康，此类场景中的恶意攻击可能导致严重损害甚至生命损失。

面对保护无线传感器网络的安全这一挑战，研究人员已为这些平台提出了新的安全解决方案。相关文献十分丰富，我们只能列举少数几个例子[卡尔洛夫和瓦格纳 2003；佩里格等 2004；杜等 2005；刘和宁 2008；汗和阿尔加特巴尔 2010]。大多数研究集中在针对物理层和网络层威胁的解决方案上，例如干扰攻击、对路由协议的攻击以及传输中数据的机密性和完整性。另一类工作是软件认证，用于评估节点完整性，特别是检查节点是否运行预期的软件[塞沙德里等 2004；朴和申 2005；塞沙德里等 2006；张和刘 2010]。

尽管存在此类解决方案，针对无线传感器节点的许多攻击仍然可能发生。例如，攻击者可能通过物理接口破坏节点，或篡改节点硬件本身，以在网络中引入错误测量值。这将使文献中提出的许多解决方案失效，因为受损传感器上的加密材料（在缺乏可信硬件的情况下）将对攻击者暴露。即使传感器难以接触或篡改，攻击者仍可能通过局部操控感知环境来破坏测量值，从而引发恶意读数，例如使用打火机触发火灾报警器。我们将所有这类攻击称为恶意数据注入。其目的是通过生成关于感知现象的虚假信息，破坏无线传感器网络的任务，造成潜在的灾难性后果。特别是，攻击者可能试图
—引发不适当的系统响应，例如，触发电网过载，导致部分关闭；或者 —掩盖期望的系统响应， 例如，使入侵警报失效。

由于此类攻击可能带来的影响，防范这些攻击变得至关重要，而本综述重点关注了能够解决这一问题的已有方案。检测恶意数据注入的主要挑战在于找到足够的攻击证据。一种可能的方法是通过软件认证来寻找传感器本身被篡改的证据，如前所述。然而，软件认证在实际部署中存在困难（例如，由于时效性约束和设备硬件限制[Castelluccia et al. 2009]）。此外，仍有可能发生对感知环境进行局部修改的攻击。另一种方法是通过流量分析[Buttyan and Hubaux 2008]，寻找传感器之间通信中流量模式变化的证据。尽管这种方法在检测网络层攻击（特别是路由攻击）方面有效，但通常无法检测恶意数据注入，因为攻击者可能修改传感器报告的值，而不改变传感器之间通信的流量模式。

出于这些原因，本文重点关注那些在传感器测量值本身中寻找受损证据的技术，无论这些测量值是如何被受损的。因此，本综述将涵盖对这些测量值进行数据分析以检测恶意干扰的技术。此外，我们包括旨在检测无线传感器网络中的通用异常但仍基于收集的测量值的论文。相反，基于网络参数（如数据包传输率、数据包丢弃率、传输功率等）的异常检测技术不在本综述的范围内。事实上，恶意数据注入检测的一个关键方面是构建数据期望模型，即能够定义对传感器测量值期望的模型。在此背景下，异常出现在数据本身固有的相关结构中，这些相关结构无法在网络参数中找到，并且可能在不干扰网络参数的情况下发生。

本调查所审阅的所有论文均假设攻击者旨在造成明显的不良影响，并注入在当时当地与应报告的正确值以某种可检测方式不同的测量值。这一假设使得可以利用数据分析来检测数据注入。然而需要注意的是，被破坏的传感器应报告的真实值无法直接观测。相反，只能通过其他传感器报告的值等间接信息对其进行表征，而这些间接信息可能不足以检测出破坏行为。当存在故障或自然发生的事件时，间接信息本身也可能不准确，这使得问题更加复杂。故障指的是任何类型的真正错误，无论是瞬态还是非瞬态，且可能难以与恶意注入区分开来。事件指的是感知现象中的显著变化，例如火灾、地震等。我们将区分恶意数据注入与事件和故障的问题称为诊断，并回顾该问题的最新研究方法。另一种导致间接信息不可靠的原因是存在共谋传感器，即多个被破坏的传感器以协调的方式生成恶意值。在这种情况下，攻击者对系统的控制力增强，从而可能引发新的、更有效的攻击。

检测和诊断恶意数据注入是确保感知数据完整性这一更普遍问题的一个子集，感知数据可能因故障或其他原因遭到破坏。这一点在所调研的研究中有所体现，许多旨在检测故障传感器或错误数据的技术也被推荐用于恶意数据注入的检测。相比之下，仅有少数论文明确关注恶意数据注入。然而，故障与恶意注入的数据之间存在显著差异，因为后者是以复杂方式故意制造的，以增加检测难度。因此，有必要进行一项综述：（1）分析针对恶意数据注入的相关工作的成果与不足；（2）回顾为非恶意数据篡改提出的最先进的技术，并评估其在此问题上的适用性。

在无线传感器网络的背景下，适用的最新研究大致遵循两种方法：异常检测技术，始于约2005年[塔纳猜威瓦特和赫尔米 2005] ；以及信任管理技术，始于约 2006[张等人 2006]。我们回顾了这两种方法的最新研究进展，并根据所调查的研究进行了比较
—采用的方法，—检测恶意数据注入的能力，以及— 结果和性能。

本文的其余部分组织如下。在第2节中，我们描述了与本文相关的现有综述。在第3节中，我们回顾了有助于理解本文其余部分的相关概念。在第4节中，我们分析了定义传感器测量值预期行为的可能方法，并分析了最先进的技术中采用的不同方法。在第5节中，我们分析了最先进的检测算法。在第6节中，我们描述了两个重要的方面应对恶意数据注入问题，超越检测：攻击的诊断与特征分析。在第7节中，我们给出了所调研技术及其实验结果的对比表格，并附有简要讨论。最后，在第8节中，我们提出了本研究的结论以及暴露出的未解决问题。

2. 相关综述

据我们所知，目前尚无关于检测无线传感器网络中恶意数据注入技术的综述。然而，已有若干相关综述，我们在此部分对其进行讨论。

Boukerche 等人[2008]分析了无线传感器网络中安全定位算法的技术。恶意数据注入与对定位系统的攻击之间存在一些相似之处，因为传感器的位置可以被视为一种特定的被感知物理现象。然而，Boukerche 等人[2008]所描述的技术在许多方面都针对定位问题具有特异性。特别是，拓扑结构、无线电传输功率和延迟方面的约束为检查传感器报告信息的一致性提供了明确的标准。相比之下，我们的重点是那些不需要预先了解被监测物理现象即可检查数据一致性的技术，而是通过直接分析数据本身来推断相关性。

拉贾塞加拉等人 [2008] 回顾了11篇关于无线传感器网络中异常检测的前沿论文。尽管他们重点关注入侵检测，但该综述还涵盖了消除错误读数和降低功耗的内容。所调研的检测算法同时考虑了传感器测量值、网络流量和功耗。相比之下，我们的关注点更为具体：恶意数据注入的检测。我们覆盖了更广泛的文献，因为我们不仅包括异常检测以外的技术，还描述了检测恶意数据的进一步步骤，并纳入了自那以来大量新发表的相关研究。

Xie 等人[2011]对无线传感器网络中的异常检测进行了综述，重点在于无线传感器网络架构（分层/平面）和检测方法（统计的、基于规则的、数据挖掘等）。他们以与我们类似的方式描述了检测流程：定义一个“正常轮廓”（即我们所指的正常或预期行为），并通过测试来判断是否存在异常以及异常的程度。然而，我们的综述是基于对正常行为的定义以及基于该定义进行检测的方法来组织的，而 Xie 等人[2011]仅关注后者。这一选择使我们能够根据数据的正常表现形式，明确特定检测技术被采用的动机。此外，Xie 等人 [2011],未分析将异常分类为攻击的诊断过程，而该诊断过程是本综述的重要组成部分。

一些综述讨论了无线传感器网络（WSN）安全中的信任管理（例如，Lopez 等人 [2010], ¨Ozdemir 和 Xiao[2009],以及 Sang 等人[2006]）。然而，这些综述主要关注通过网络层进行的攻击，而对恶意数据注入的关注较少。Yu 等人 [2012]列出了可通过信任管理缓解的所有威胁，包括“隐蔽攻击”——一种恶意数据注入，但并未对其进行详细分析。类似地，Zahariadis 等人 [2010a]构建了信任度量分类，其中包含报告值/数据的一致性，但他们主要关注其他与网络相关的度量。此外，Shen 等人[2011]综述了针对网络层攻击的防御策略。特别是，这些策略源自博弈论，并考虑了攻击者为平衡攻击带来的声誉收益与损失所能采用的策略；而在我们的综述中，我们则专注于分配和维护此类声誉的技术。

与本文最接近的综述是 Jurdak 等人 [2011]。它描述了用于检测由环境因素（例如，传感器附近的障碍物或节点硬件/软件问题。他们对异常检测的描述与我们的相似，但两篇综述在所考虑的异常性质上有显著差异：我们关注的是攻击，而他们关注的是故障。Jurdak等人[2011]还声称，可以通过传感器之间的空间或时间比较来检测异常，因为多个传感器同时出现校准偏差或失效的可能性很小（假设不存在组故障）。这一假设将异常（故障）视为独立事件，但在存在恶意数据注入的情况下不成立，特别是当被破坏的传感器之间发生共谋时。

3. 初步介绍

下文将描述无线传感器网络中传感器测量值的收集方式。我们还将介绍迄今为止用于检测恶意数据注入的两种方法：异常检测和信任管理。

3.1. 数据聚合方案及其影响

无线传感器网络的典型工作流程始于通过连接到无线节点的传感设备测量物理现象，然后将测量值通过网络传送到数据汇聚点。数据汇聚点（例如基站）收集并聚合这些测量值后，可对数据进行解释或传输到远程站点。然而，数据也可以由网络中的中间传输节点在传输过程中进行聚合，聚合架构有多种可能的变化形式。不同方案之间的选择基于优化电力效率、设备数量、物理空间覆盖范围等标准。根据这些标准找到最优架构仍然是一个重要的研究挑战。

早期工作认为所有原始测量值都被收集到基站，由基站在那里执行数据融合和其他计算 [Shepard 1996；Singh 等人 1998]。此后，特别是随着 LEACH 协议的引入 [Heinzelman 等人2000],，架构变得越来越具有层次性。LEACH 采用单层层次结构，其中传感器被组织成簇，并与簇头通信，而簇头再与基站通信，如图1所示。基于簇的协议，尤其是那些簇在时间上动态变化的协议[Heinzelman 等人 2000],，已被证明在与基站通信需要多跳传输时更加节能[Heinzelman 等人 2000]。

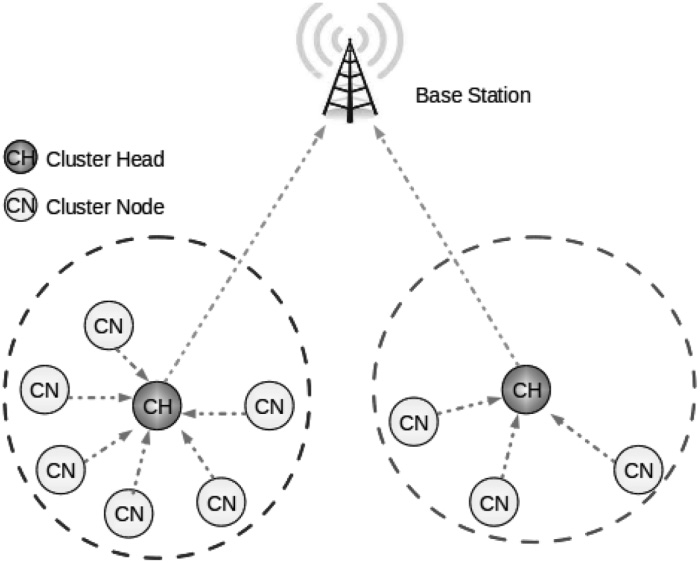
LEACH中引入的单层层次结构可以推广到基于树的结构，如法索拉等人[2007]所述。中间树节点可能只是将不同源生成的数据包合并为一个数据包，而不对数据进行处理。这被称为无尺寸缩减的网络内聚合[法索拉等人 2007]。或者，它们通过应用聚合算子（例如，均值、最小值、最大值）来处理传感器测量值，这被称为in-network aggre-gation with sizereduction[法索拉等人 2007]。因此，簇头承担了额外的计算负担，以最小化传输的数据。本质上，这种做法用计算的功耗换取通信的功耗，但由于在无线传感器网络中通信消耗的电力要大得多，因此这种权衡通常是有利的。

有关无线传感器网络架构以及数据聚合执行位置的信息对于将检测任务分配给无线传感器网络节点至关重要。例如，如果使用了具有尺寸缩减的网内聚合，则基站无法分析所有的测量值，此时聚合节点必须协助基站完成检测任务。在这种情况下，还必须确保这些节点上聚合过程的完整性[普日达特克等人 2003；加内里瓦尔和斯里瓦斯塔瓦 2004；罗伊等人 2014]。

3.2. 与异常检测和信任管理的关系

恶意数据注入的检测目前已通过两种主要方法来解决：异常检测（例如，塔纳猜维瓦特和赫尔米 [2005],、刘等人 [2007], 以及孙等人 [2013]）和信任管理（例如，阿塔克利等人 [2008],、包等人 [2012], 以及吴等人 [2012]）。虽然异常检测通过定义正常行为来推断异常的存在，但信任管理则是评估传感器行为为正常的置信水平（可信度）。当受损传感器偏离其预期行为时，其获得的信任值将较低。尽管异常检测同样基于对预期行为的定义—— “异常检测指的是发现数据中不符合预期行为的异常情况” 钱多拉等人 [2009]——但这两种方法在如何解释偏差方面有所不同。在信任管理中，以传感器为粒度分析传感器的测量值，每个传感器都有一个信任值，并随时间逐步更新。而异常检测方法则在粒度上没有限制，可从单次测量到整个系统进行应用，通常通过定义预期行为的边界，将超出该边界的的一切视为异常的。

鉴于这两种方法之间的相似性和差异，我们将接下来的两节内容结构安排如下：在下一节中，我们将描述如何收集有关预期数据的信息，而不论其是用于异常检测还是信任管理。而在第5节中，我们将分别针对异常检测和信任管理，描述如何检测与预期数据的偏差。

4. 预期数据建模

在我们的研究背景下，expected data指的是的一组用于表征未受恶意注入影响的测量数据的属性。由于此前尚无针对此问题的综述，我们首先引入无线传感器网络感知的通用表述。这使我们能够分析预期数据的不同模型，并使用一致的术语来描述相关工作，因为不同文章中所使用的术语常常存在差异。

4.1. 问题的特征分析

我们专注于解释数据，并抽象出与实现相关的问题（如传感器之间的同步）以及与网络相关的问题（如数据包丢失或延迟）。我们考虑一个部署区域D，其中布置有一组N个传感器。每个传感器测量诸如温度、风速、水质、电力和气体流量等物理属性。传感器的测量过程具有一定程度的不确定性，这可能是由于噪声、故障和恶意数据注入所导致的。为了消除这种不确定性，我们引入一个理想函数 ϕ，它表示在没有任何不确定性源的情况下传感器读数的值。

该函数的自变量是空间中的点s以及读数对应的时间瞬时t，如公式（1）所示：
$$ \phi(s, t) \quad s \in D, \forall t. \quad (1) $$

我们将此函数称为物理属性函数。在位置si部署的通用传感器i在时间t产生的读数，是对在 (si,t)处评估的物理属性函数的某种近似。因此，通用传感器的读数可以建模为一个函数Si， 该函数将一个通用的测量误差 ε(si,t)添加到物理属性上，而该物理属性可能随时间和空间发生变化。公式(2)将函数Si定义如下：
$$ S_i(t)= \phi(s_i, t)+ \epsilon(s_i, t) \quad i \in 1,…, N. \quad (2) $$

请注意，传感器读数是唯一的可观测量；物理属性和测量误差都无法直接观测。当发生恶意数据注入时，部分传感器读数也会变得不可观测，因为攻击者用伪造的测量值替换了真实的测量值。因此，需要利用某些可观测量的相关信息来描述真实的测量值。如果这些相关信息能够帮助我们区分数据注入，且其自身不易受到注入影响，则该过程是有效的。

通过可观测属性来描述不可观测的真实测量值是一个建模过程，该过程对数据的描述方式做出假设。例如，传感器产生的测量值可以建模为来自正态分布 [张等人 2006] 的样本。假设受损节点产生的数据不符合正态分布，则该模型能够区分被攻陷节点 [张等人 2006]。

将问题与模型关联的关系是一种一对多关系。同一问题的不同模型并不等价，选择一个好的模型对性能至关重要。特别是，一个好的模型应具备以下特征：
—准确性– 没有模型是完美的，每个模型实际上都是一种近似。准确的模型能够最小化近似误差。—适应性– 传感器测量的物理属性在时间上发生变化。因此，模型应能适应动态变化的环境。—灵活性– 良好的模型应具备灵活的应用能力，不受具体应用的限制。这类模型应尽可能抽象出更多细节，仅捕捉所需的关键属性。

这些理想的特性彼此之间存在冲突：准确性可能通过特定上下文的细节更好地实现，但这会限制灵活性并损害适应性。一个显著影响准确性和灵活性的适应性要求是传感器的移动性，因为当传感器节点迁移到新的位置时，先前的期望将不再成立。事实上，传感器迁移对应于公式(2)中si的变化，这可能会改变所有测量值的时间序列，仅留下传感器特有噪声作为唯一不变的因素。

支持移动性。尽管移动性并不是恶意数据注入检测中直接涉及的一个方面，但某些技术比其他技术更适合支持移动的传感器。特别是那些在邻域内比较测量值而不考虑过去行为的异常检测技术（例如，Handschin 等人 [1975],魏 等人 [2006],刘等人 [2007], Wu 等人 [2007],和 郭等人 [2009]），通常能够适应移动性，因为每个时间点都会提取新的期望。然而，这类技术也需要在存在移动性的情况下意识到拓扑变化。

具有信任信息交换的 信任管理技术 （例如 包等人 [2012], Huang 等人[2006], Ganeriwal 等人[2003],和 Momani 等人 [2008]）也适用于 移动性 场景，因为一个迁移到新区并成为 j 的 邻居 的 传感器i，可以从过去曾是 j 的 邻居 的 传感器 那里获得 推荐信息 [扎哈里亚迪斯等人 2010b]。迄今为止，信任信息交换的研究尚未深入探讨 移动性 的影响；因此，通常情况下，只有当 i 和 j 之间存在交互，且 i 无法观察到 j 的行为（例如，不在 无线通信范围 内）时，传感器i 才会保留关于传感器 j 的 间接信息 。然而，当 传感器 是 移动的 时，即使 i 和 j 从未交互过，只要它们彼此靠近，未来仍可能发生交互。只有在此时，关于 j 的 推荐信息 才会引起 i 的兴趣，因而需要一个请求此类 推荐信息 的 准则 。

本工作后续分析的现有研究在很大程度上忽略了移动性方面。鉴于上述考虑，我们得出结论：需要开展更多工作来应对传感器移动性带来的问题。

4.2. 利用相关性

由于被伪造的测量值替代的原始测量值无法直接观测，因此需要通过相关信息间接表征。两部分信息之间的关系即为相关性，该相关性可通过在线计算、历史数据或先验建模获得。在任何一种情况下，假设相关性在计算时刻与使用时刻之间未发生变化，则真实测量值与受损测量值的同时存在可能导致相关性的中断。

我们在此广泛意义上使用相关性，意指某种连续依赖关系，而不是最常用的相 关性度量——皮尔逊相关系数。用E、μ和 σ分别表示期望值、均值和标准差，则两个随机变量X和Y之间的皮尔逊相关系数ρXY由下式给出
$$ \rho_{XY}= \frac{\text{cov}(X, Y)}{\sigma_X\sigma_Y} = \frac{E[(X -\mu_X)(Y -\mu_Y)]}{\sigma_X\sigma_Y}. \quad (3) $$

请注意，该系数仅衡量两个变量之间的线性依赖关系，而可能会遗漏非线性依赖。

在无线传感器网络中，我们通常可以考虑三个不同领域中的相关性：时间的、空间的和属性领域 [Rassam 等人 2013]。
—时间相关性是指传感器读数与其先前读数之间的依赖关系。它用于建模感知的物理过程在时间上的连贯性。
—空间相关性是指同一时间来自不同传感器的读数之间的依赖关系。它对不同传感器感知感知现象时的相似性进行建模。
—属性相关性是指与不同物理过程相关的读数之间的依赖关系。它对异构物理量（如温度和湿度）之间的物理依赖关系进行建模。

通常使用这些不同类型相关性的组合。我们现在分析它们如何有助于定义预期数据。

4.3. 时间相关性

感知数据在时间上的变化可以建模为一个随机过程[Boukerche2009],，其中不同时刻的随机变量是相关的。如公式(2)所示，传感器测量值在时间上的变化取决于物理属性引入的变化和测量误差。该变化的物理属性在时间上受到某些约束，例如存在渐变或某些模式的交替，因为所观察的现象通常遵循物理定律。因此，如果以足够高的频率采集测量值，连续测量也将受到类似的约束。这一简单观察为一种识别错误（包括恶意注入）的方法提供了依据，即当时间变化不满足这些约束时，便可判断存在异常。然而，将这一观察应用于偏差检测时存在两个主要困难：过程的时间演化受不确定性因素影响，且测量值本身也受到噪声干扰。

使用卡尔曼滤波器 [Kalman 1960]对时间序列建模时，这两个因素分别被称为过程噪声和测量噪声。测量噪声通常被建模为高斯过程。而过程噪声则来源于用于描述过程动态的模型的不完善性。例如，在将过程建模为离散马尔可夫过程时，时间t1处的值可以表示为
$$ \phi(t_1)= F(\phi(t_0))+ w(t_0), \quad (4) $$
其中F对时间过程的预期演化进行建模， w是过程噪声。

使用马尔可夫过程并以卡尔曼滤波器建模，构成了孙等人提出的基于扩展卡尔曼滤波器（EKF）的算法的基础 [2013]。在此方法中，每个传感器根据其邻居的先前读数建立对邻居的预测。预测值与实际值之间的差异形成偏差，用于检测恶意数据注入。然而，作者指出，攻击者可通过引入足够小的变化来逃避EKF算法的检测。为解决这一缺陷，作者采用了CUSUM GLR算法，该算法考虑了更多时间样本上的累积偏差，并检验其是否为零均值。这一特性使得攻击者更难引入能够实现其目标的偏差。

苏布拉马尼安等人[2006]也定义了具有时间相关性的预期数据。在此，作者通过核密度估计器对时间窗口内的测量值的概率密度函数（PDF）进行拟合。给定一个新的测量值p，该 PDF提供了关于落在[p − r,p+ r]区间内（参数r取决于具体应用）的预期值数量的信息。

4.4. 空间相关性

在发生突发事件时，物理过程的动态可能会迅速变化。通常，检测此类事件（如森林火灾、火山喷发或心脏骤停）正是无线传感器网络的目的。然而，事件的发生可能会破坏时间相关性，从而引发虚假异常。尽管如此，不同的传感器节点通常会受到事件影响，并产生与事件源空间相关的测量值：因此，在事件显现期间，不同传感器的测量值之间存在相关性[Boukerche 2009]。这种现象称为空间相关性。

一些技术通过关联同一时间间隔内不同传感器的测量值来利用空间相关性——这相当于在公式（2）中固定t，并让参数i变化。最广泛使用的空间相关模型也是最简单的：它假设在没有错误和噪声的情况下，所有传感器会产生相同的测量值；也就是说，它们测量的是同一个值，我们将此模型称为空间同质spatially homogeneous[Zhang 等人 2006；Ngai 等人 2006； Wu 等人 2007；Liu 等人 2007；贝通库尔特等人 2007]。就公式（1）给出的物理属性模型而言， ϕ(s,t) 实际上仅是时间的函数。在这种情况下，传感器测量值可以用高斯分布来描述。

这是因为它们是具有明确定义的期望值和方差的随机变量的独立观测，根据中心极限定理，其值将大致呈正态分布[Rice 2007]。检测具有异常读数的传感器就变成了简单地检测与空间测量分布的偏差，且随着传感器数量的增加，分布估计的准确性也随之提高。

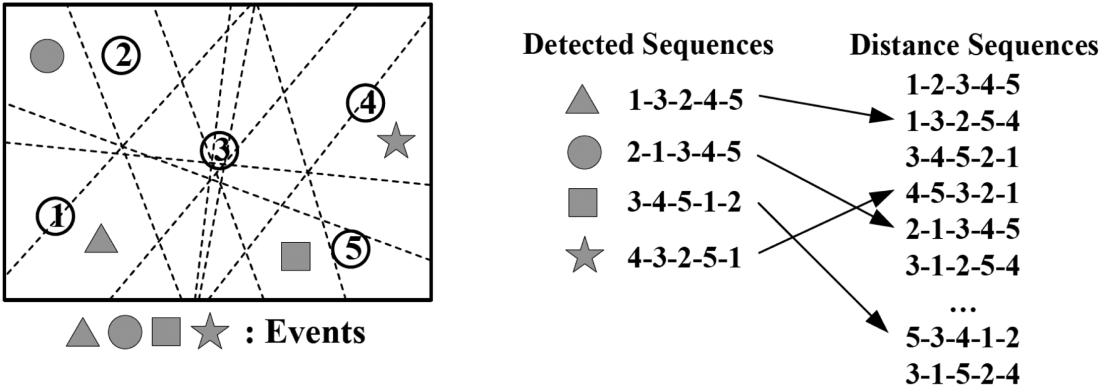
同质模型仅适用于足够小且无障碍物的空间区域。然而，当部署拓扑和物理现象的特性违反同质性假设时，空间传播规则仍可能引发空间相关性。在许多应用中，这种传播可被假设为单调的[郭等人 2009]。这意味着空间某点处的物理属性值应随着与该点距离的增加而单调递增或递减。例如，在监测森林火灾时，温度随着距火源的距离增加而单调递减。为了确定该性质是否成立，郭等人[2009]将部署空间划分为若干区域，称为面。对于每个面，作者构建一个“距离序列”，对应于按距该面距离排序的传感器序列。在感知现象过程中，传感器读数被排序以生成估计序列，然后将其与所有可能的距离序列进行比较，如图2所示。如果估计序列恰好与某个距离序列一致，则传感器测量值符合预期。该条件随后被放宽，以应对噪声测量对单调性假设有效性的削弱，但破坏其有效性的主要因素是多个同时发生的事[郭等人 2009]。

与其考虑测量值单调性这样的严格假设，不如将传感器读数之间的相关性建模为它们空间位置的函数。这类模型的一个例子是变异函数，其定义为两个位置处物理现象数值差异的方差。在我们的表示法中，两点s1和s2之间的变异函数定义为 var(ϕ(s1, t) −ϕ(s2, t))。当假设物理现象为各向同性时，变异函数仅表示为距离的函数，张等人[2012]已将其用于根据其他传感器的测量值计算预期测量值。需要注意的是，在存在障碍物的情况下，变异函数不仅与距离有关，还依赖于绝对位置。

与其考虑传感器之间的距离，空间相关性可以计算为传感器值本身的函数。这种选择适用于距离相同但受到不同噪声或空间障碍物影响的传感器。然而，当传感器具有移动性时，这会导致需要进行相关性更新。例如，Sharma 等人 [2010] 将一个传感器的测量表示为其他传感器测量值的线性组合，提取该函数的参数，并推导出预期传感器读数。Derezynski 和 Dietterich [2011], 则通过拟合来自N个传感器的测量值的联合概率分布来推导预期读数，假设该分布为N元高斯分布。请注意，这种方法也隐式地假设了一个线性模型，因为两个随机变量之间的协方差捕获的是线性依赖关系（我们在第4.2节中提到过，这对于皮尔逊相关系数是成立的，而皮尔逊相关系数只是协方差指数的一种归一化形式）。

空间相关性经常与时间相关性结合使用，因为它们能够捕捉不同类型的偏差。例如，贝通库尔特等人[2007]提出了一种基于两种差异的异常检测技术：一种是传感器当前读数与其自身先前读数之间的差异（时间相关性），另一种是同一时刻不同传感器读数之间的差异（空间相关性）。通过这两种差异的分布，来判断数据样本在时间域和空间域中是否具有统计显著性。

4.5. 属性相关性

在同一无线传感器网络中，观测不同物理属性（如光、振动、温度等）的传感器可能共存。由于这些物理属性之间存在物理关系，它们中的某些属性可能存在相关性，例如温度和相对湿度。通常，在每个部署位置，si个负责测量不同物理过程的不同传感器连接到单个传感器节点。如公式(5)所述，对于空间和时间上的固定点，我们有一组A个物理属性。我们将属性相关性定义为它们之间的相关性：
$$ \phi_a(s, t) \quad a \in 1,…, A. \quad (5) $$

我们期望在传感器节点报告的测量值中也能观察到属性相关性。然而需要注意的是，属于同一节点的传感器之间的属性相关性并不具备信息价值，因为攻击者一旦攻破一个节点，就可能篡改该节点上收集的所有测量值。但是，当空间冗余有限时，基于属性的期望与空间相关性结合使用则非常有用。例如，用于医疗保健的体域传感器网络由于在患者身上部署多个传感器不切实际，因此冗余度有限。此时，我们仍可利用不同传感器节点测量的不同生理值（即属性）之间的相关性。

萨勒姆等人[2013],在医疗保健领域提出了一个示例，他们利用空间属性相关性和时间相关性。基于离散小波变换，将属性信号分解为平均信号和波动信号。通过汉佩尔滤波器检测波动信号能量中的突变时间变化，从而标记异常属性。该技术被提出用于容错事件检测，其依据是：由于属性相关性，在事件发生时预计会有多个属性同时被标记。如果未达到最少数量的异常属性，则认为报告异常读数的传感器有故障。然而，在恶意数据注入的情况下，该技术无法阻止攻击者故意注入破坏事件检测的测量值。

4.6. 提取预期数据的技术概述

在前面的章节中，我们分析了不同类型的相关性、它们所捕获的信息，以及文献中提出的技术在利用相同相关性方面的变化。我们在表I中总结了这一分析。

表I. 相关类型

相关性	信息	Type	捕获	变化
时间的	corr(ϕa(s, t1) ϕa(s, t2))	— 时间序列演化模型 — 时间记忆（用于建模相关性的W的最大值）	相关性被建模）
空间	corr(ϕa(s1,t) ϕa(s2, t)) — 空间模型，例如同质的、单调的 变异函数，线性依赖 — 相关变分模型，例如距离依赖， 传感器依赖，固定 — 邻域选择准则
属性	corr(ϕa1(s, t) ϕa2(s, t))	— 相关性提取过程，例如从物理定律中提取 时间/空间分析等

5. 检测与预期数据的偏差

关于实际测量的期望可用于计算报告的测量值与期望之间的偏差。异常检测和信任管理都需要期望，但它们使用不同的准则来应对异常数据。具体而言，异常检测使用期望来区分异常数据和正常数据。而信任管理则使用某种准则将与预期数据的偏差映射为一个信任值。由于这两种技术在解释偏差的方式上有所不同，我们将在本节中分别讨论它们。

5.1. 异常检测技术

异常检测是一种将数据表征为正常或异常的方法。与Rajasegarar等人[2008],将异常值检测和异常检测视为等同不同，我们认为异常值检测只是属于异常检测类别中的一种技术。原因是异常值检测识别的是那些不太可能出现的样本，而测量值可能在其他标准下表现为异常，这种异常不能简单归结为寻找异常值的问题。例如，考虑一个传感器出现stuck at故障的情况：即它始终产生相同的测量值。对来自该传感器最近的一组测量值应用异常值检测技术时，不会检测到任何异常值。然而，异常依然存在，可以通过考虑测量值分布中的低方差等方式进行检测。为了阐明这一点，我们介绍了用于异常检测的统计检验方法，并强调其与更传统的异常值检测技术之间的差异。随后，我们深入探讨异常值检测技术，这仍然是目前最常用的异常检测方法。

5.1.1. 统计检验

基于统计检验的技术假设了概率数据分布。然后将实际数据与该分布进行比对，以验证其是否符合该分布。基于统计检验的技术比异常检测更通用，因为它们同时检查异常值和非异常值对分布的符合性，而异常检测则侧重于单个数据样本的类别划分。

例如，雷兹瓦尼等人 [2013]采用基于统计检验的技术来检测恶意共谋节点。他们假设空间同质性，并将传感器测量值建模为真实值加上一些噪声。真实值通过测量值的加权平均进行估计，估计值与每个测量值之间的差异被假定为正态分布。该假设符合

中 心极限定理[Rice 2007]的应用——误差被认为由大量独立因素引起，因此遵循正态分布。随后通过正态分布的符合性评估来判断柯尔莫哥洛夫‐斯米尔诺夫检验，用于量化经验分布（误差分布）与参考分布（正态分布）之间的距离。

5.1.2. 异常检测

异常检测方法将位于大多数数据样本所在空间之外的数据视为异常数据。只要恶意注入的值在数据集中占少数且显著偏离其他数据，该技术就能相对有效地识别恶意数据注入。

从历史上看，异常检测在无线传感器网络中已被提出用于不同的目的，有时目标甚至相互对立：在某些情况下，这些技术旨在滤除异常值，而在其他情况下，异常值本身才是主要关注点。例如，滤除异常值可以提高数据准确性 [Janakiram 等人 2006]以及实现节能 [Rajasegarar 等人 2007]。以异常值为主要关注的应用包括故障检测[Paradis 和 Han 2007],、事件检测 [Bahrepour 等人 2009；张等人 2012],以及恶意数据的检测。接下来，我们将描述异常检测问题的不同方法，

5.1.2. 异常检测（续）

不考虑具体应用背景，但重点介绍那些可用于检测恶意数据注入的技术。

基于最近邻的异常值检测。 在基于最近邻的异常检测中，异常值是指具有狭窄邻域的数据样本，其中邻域包含在特定距离内的数据样本。无线传感器网络中的大多数基于最近邻的技术都受到著名的LOCI方法[Papadimitriou等人 2003],的启发，该方法为每个样本计算在由半径 αr表征的数据空间内的邻居数量，其中 α是用于降低计算复杂度的参数。与邻居平均数量的相对差异，即在数据空间中半径r范围内的样本数量，构成了多粒度偏差因子(MDEF)。MDEF会与一个等于MDEF标准差3倍的阈值进行比较，以确保当数据样本之间的距离服从高斯分布时，超过阈值的值少于1%（对于其他分布，该百分比可上升至10%）。需要注意的是，通过将传感器的测量值视为数据样本，该方法可适用于恶意数据注入的检测。然而，由于需要为每个新数据样本计算其邻居，这类方法具有较大的计算开销，研究界似乎对基于最近邻的方法已略有失去兴趣。

基于聚类的异常值检测。 聚类是另一种常用于异常检测的技术。在此方法中，将相近的元素组织成簇后，远离其他元素的元素即为异常值。例如，拉贾塞加拉等人[2006]认为，如果一个簇与其他簇之间的距离大于该簇元素到均值距离的标准差，则将其识别为异常簇。

基于PCA的异常检测。 主成分分析（PCA）[Marsland 2009]是一种常见的数据分析技术，也被用于发现异常值[Chatzigiannakis 和 Papavassiliou2007]。PCA 基于将k维数据空间投影到另一个k维数据空间，其中描述数据样本的变量是线性无关的。该变换的定义方式使得投影后的变量按方差降序排列。k个变量中的前p个被定义为主成分，并可被投影回原始数据空间以获得预测向量ynorm[Jackson 和 Mudholkar 1979],，也称为正常数据[Chatzigiannakis 和 Papavassiliou 2007]。原始数据与正常数据之间的差异构成残差向量y res。当残差向量的幅值较大时（即残差向量的平方预测误差 SPE= ‖yres‖ 2超过阈值），被视为对预测（正常）向量的偏差，并被认为是异常值[Chatzigiannakis 和 Papavassiliou 2007]。PCA 可应用于k维数据集，例如由k个测量值的时间序列组成的数据集。

传感器 [查齐安纳基斯和帕帕瓦西里乌 2007]。在这种情况下，yres反映空间相关性的变化，但相同的概念也可应用于时间或属性域。

基于分类的异常检测。 传统的分类技术学习如何识别来自不同类别的样本。异常检测考虑两类：异常和正常；然而，与正常数据样本相比，异常数据样本很少能被观察到。因此，异常检测的分类通常被简化为仅基于正常样本观测的单类分类问题。

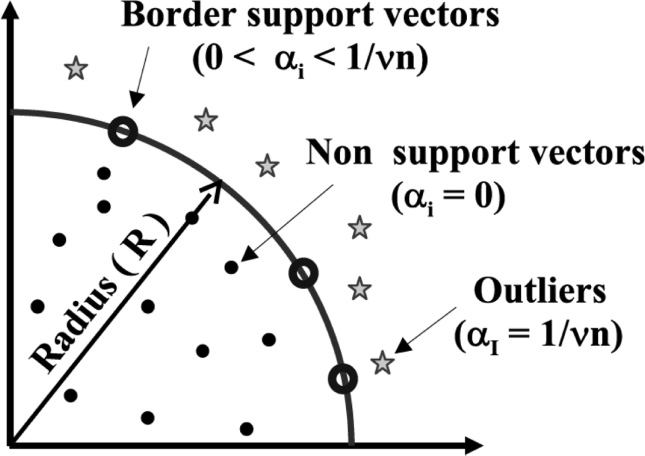
正常和异常样本可以被视为数据空间中两个不同区域内的点。找到分隔这两个区域的边界可能是不可行的，因为这些区域存在重叠，即使存在边界，其形状也可能非常复杂。支持向量机（SVM）是一种分类技术，可以通过将数据样本投影到高维空间来克服这一限制。在投影后的数据空间中，即使原始空间中不存在这样的边界，也可能存在一个能够分离正常点与异常点的边界，或者该边界具有更简单的形状。例如，正常样本可能被包含在投影数据空间中的一个球体内。当数据空间仅包含正值时，该问题简化为一种特殊类型的 SVM，称为一类四分之一球面支持向量机[Laskov 等人 2004],，如图3所示。采用这种方法，分类问题就转化为寻找球体半径的问题。根据无线传感器网络（WSN）数据集输入到四分之一球面支持向量机的方式，分类可以在其时间域 Rajasegarar 等人 [2007],、属性域，或两者同时进行 Shahid 等人 [2012]。

贝叶斯网络还被应用于无线传感器网络中，以基于分类的方法检测异常值。贝叶斯网络通过网络图定义随机变量之间的条件独立性关系。在无线传感器网络中，随机变量可以是物理属性在空间和时间上的不同值。

Dereszynski和Dietterich [2011]给出了贝叶斯网络在无线传感器网络中的一个应用实例。物理属性 ϕ(si, tk)被建模为一个随机变量，其依赖于 ϕ(si,tk−1)（一阶马尔可夫关系） 以及不同位置的值 ϕ(sj≠i,tk)。目标是确定传感器的状态，该状态被建模为一个具有两个可能值的随机变量：正常工作和损坏。通过关于状态变量最大化测量值的后验概率（该后验概率取决于物理属性和传感器状态变量），以识别故障节点。Dereszynski和Dietterich [2011]在评估其方法时假设故障传感器的测量值方差显著增加（增加105），这一假设的依据是观察到故障传感器的测量值显得更加嘈杂。尽管该假设在故障情况下是合理的，但对于数据注入通常不成立，其中攻击者可以任意选择测量值的分布，并且在大多数情况下希望不被发现。

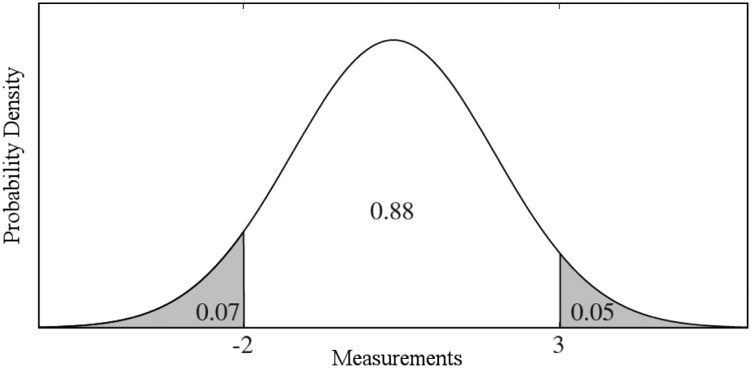
统计异常检测。 统计异常检测通过统计分析样本概率分布尾部的数据特征来识别离群数据样本，如图4所示。

需要注意的是，这种方法不同于基于统计检验的异常检测，因为它并不检验样本是否符合其预期分布，而只是识别出位于分布尾部的异常值。例如，可以将远离均值的样本定义为异常值。魏等人[2006]已将这一思想应用于来自不同传感器的测量，从而利用了空间相关性。来自N个不同传感器的测量值的空间样本均值ˆμS定义为
$$ \hat{\mu} S= \frac{1}{N} \sum {j=1}^{N} S_j(t). \quad (6) $$

魏等人[2006]使用它来评估传感器j相对于空间均值的偏差，与均值本身的大小进行比较，采用的度量指标为
$$ f(j, t)= \sqrt{\frac{(S_j (t)-\hat{\mu}_S)^2}{\hat{\mu}_S}}. $$

类似地，塔纳猜维瓦特和赫尔米 [2005]使用度量 t∗= Si (t)−(μTi± δ)STi /√W，其中 μTi 和 STi 分别是传感器 i 在大小为 W 的窗口中的时间均值和样本标准差，而 δ 是由于观测现象的空间传播所导致的传感器 i 与 j 之间已知的变化。根据第4.1节中的模型，一个通用传感器 j 在宽度为 W 的时间窗口 [tK−W+1,tK] 内计算其 时间的 样本均值为
$$ \hat{\mu} {Tj} = \frac{1}{W} \sum {n=0}^{W-1} S_j(t_K-n). \quad (7) $$

时间的标准差则被计算为
$$ S_T= \sqrt{ \frac{1}{W -1} \sum_{n=0}^{W-1} (S_j(t_K-n)- \hat{\mu}_{Tj}) }. \quad (8) $$

将t∗的值与设定为3的阈值进行比较，因为在正态分布的数据中，这涵盖了大约99.7%的总体（对于其他分布，该百分比下降到90%）。

在某些情况下，中位数比均值更受青睐，因为前者具有对异常值不敏感的优点。事实上，异常检测中的一个问题是如何从受异常值影响的数据中找出一般的（非离群）趋势。均值对异常值敏感，因为其与每个操作数的大小成正比。而中位数则选取一个元素来代表所有其他元素。Wu 等人 [2007] 使用中位数算子来聚合邻域内传感器的测量值。我们可以将其称为空间中位数。如果我们将 N 个传感器在时间 t 的测量值排序为 S1(t) ≤S2(t) ≤ ··· ≤SN(t)，则空间域中的中位数计算如下：
$$ \tilde{\mu} S=\begin{cases} S {(N+1)/2}(t) & \text{if } N \text{ is odd} \ S_{N/2}(t) & \text{if } N \text{ is even}. \end{cases} \quad (9) $$

在计算中位数与每个值之间的差异后，存在两种可能性：将每个差异与测量值的大小进行比较，或将差异与差异的总体分布进行比较。杨等人[2006]和吴等人[2007]在假设差异服从正态分布的前提下检测差异中的异常值。贝通库尔特等人 2007]则不依赖于高斯分布的假设，而是通过数据估计概率分布[。

在感知多个物理属性时，可以考虑所有属性上测量值的联合分布，而不是每个属性单独的分布。这种方法有可能检测到单独处理各属性时无法发现的异常值。刘等人[2007]利用基于属性间相关性的马氏距离来组合不同的属性，该方法定义了数据在属性空间中的统计分布情况。该方案如图5所示。

5.2. 基于信任管理的技术

信任管理考虑两类实体之间的可信度：信任方和受信者。信任方根据受信者的行为与预期行为的匹配程度，为其分配一个可信度值。可信度值通常在[0, 1],范围内，当受信者表现出偏离预期行为时该值降低，当受信者的行为符合预期时该值增加。

信任管理可有效地应用于无线传感器网络，以降低注入恶意数据的受损传感器节点的影响。事实上，如果预期行为能够准确描述正常节点，则当节点行为偏离该预期时，受损节点将被赋予较低的可信度值。由于信任值是在某一区间内定义的连续度量，因此无法直接对受损节点和正常节点进行分类。相反，信任值用于根据判断传感器已被攻陷的置信度施加相应的惩罚机制。需要注意的是，只有当置信度足够高时，受损节点的影响才会变得可以忽略不计。过滤

所有可信度低于给定阈值[孙等人 2012]的传感器可能有助于缓解这一缺点，但需要一种方法来设置适当的阈值。

5.2.1. 基于事件的技术

针对感知数据的信任管理最初被提出作为网络层信任的补充，即节点在执行网络层任务（如通信路由、参与路由发现过程、路由传入数据包等）时的可信程度[Ganeriwal 等，2003；Raya等人2008年；Momani 等人 2008]。对于每一项此类任务的行为可以分为两种：协作的和不协作的。

关于感知数据的首批信任管理示例采用类似的二元评估方法来构建可信度，该可信度是相对于事件检测过程定义的。首先，决策逻辑通过结合感知数据和信任值来确定事件的存在。然后，将感知数据与最终决策进行比较，以衡量传感器的协作性并更新信任值。该准则基于以下假设：邻近传感器在事件存在方面应保持一致，这是一种空间相关性形式 （参见第4.4节）。

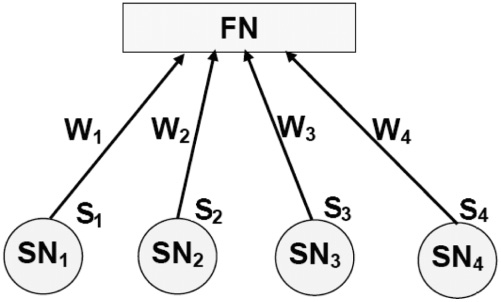
阿塔克利等人 [2008] 描述了最早采用该方法的技术之一。如图6所示，通用传感器i的读数Si(t)可取0和1值（事件的不存在/存在），这些读数被传送到一个转发节点。该节点计算∑N n=1 WnSn(t)，其中Wn: n∈1…N表示信任权重。该结果用于确定真实值E。随后，权重将按照以下规则进行更新：
$$ W_n=\begin{cases} W_n - \theta r_n, & \text{if } S_n(t) \neq E \ W_n, & \text{otherwise}, \end{cases} \quad (10) $$
其中rn是输出不同的传感器数量与传感器总数之比， θ是用于确定检测时间与准确性之间的权衡的惩罚权重。总之，可信度值（即权重）是根据测量值与聚合值的一致性计算得出的。由于过去表现出不一致（例如恶意）读数的传感器对聚合过程的贡献较小，因此聚合值比单个读数更可靠。最后，通过将权重与阈值进行比较来检测恶意节点，作者经验性地将该阈值设为0.4。需要注意的是，该算法容易受到开-关攻击的影响：一个节点在一段时间内表现良好从而获得高可信度值，随后突然开始出现故障 [孙等人 2006]。

为了应对开‐关攻击，吴等人[2012]和Lim 和 Choi[2013]提出通过一个量 α对Sn(t) ≠ E进行惩罚，并通过一个量 β对Sn(t)= E进行奖励 β< α。随着 α β 增大，有故障和恶意的节点会被更快地过滤掉。然而，具有瞬态故障的传感器也会被过滤掉，即使它们之后可能报告正确的测量值。为了避免这种情况，比率α β 还需要考虑瞬态故障的概率及其持续时间分布。因此，该操作仅能减少攻击者在开‐关攻击中切换“良好”和“不良”行为的频率。

当所有信任权重的总和等于1时，传感器读数的加权和对应于加权平均值。如前一节所述，均值的缺点是与极端读数成正比。因此，在基于信任的聚合中，中位数可作为更鲁棒的聚合算子。王等人[2010]在声学目标定位的背景下应用了信任加权中位数，其中中位数能够滤除错误测量。当高权重元素具有极端值时，使用加权中位数的优势更加明显。实际上，尽管加权平均值会偏向该极端值，但如果其他值不是极端值且它们的权重之和大于该极端值的权重，则加权中位数仍能将其滤除。这一特性降低了开‐关攻击的有效性。

另一个需要考虑的方面是事件存在的不确定性。Raya 等人[2008]通过使用基于德姆斯特‐谢弗理论（DST）的决策逻辑来处理这一问题，该方法将传感器节点的个体信念进行组合，以表达对事件存在的信念。DST 将支持事件的传感器信息与不反驳事件的信息（可能符合事件存在的不确定边界）结合起来。

5.2.2. 基于异常的技术

其他信任管理技术不分析事件决策逻辑输出的合规性，而是采用类似于异常检测的技术来查找异常行为。

事实上，异常检测的输出本身可用于定义协作/不协作行为[Ganeriwal 等人 2003],，但一种更灵活的方法是基于异常分数来更新信任值，而不是将观测限制为二元值。巴诺维奇等人[2010],给出了一个使用自组织映射（SOM）的例子。SOM 是一种聚类和数据表示技术，可将数据空间映射到离散二维神经元格网。巴诺维奇等人[2010]构建了两个 SOM 格网：一个在时间域，另一个在空间域。信任值的分配基于两个异常分数：测量值与 SOM神经元之间的距离，以及分配测量值的神经元与其他SOM神经元之间的距离。该算法的主要缺点是其计算时间。为了获得更高的准确性，SOM 需要大量神经元，但这会显著增加计算时间[McHugh 2000]。

另一个例子由张等人[2006],给出，他们使用统计检验方法（参见第5.1.1节）为传感器分配声誉值。在时间上收集的测量值被假定大致遵循正态分布。正常分布与实际测量值分布通过Kullback‐Leibler散度Dn进行比较，该散度用于评估当一个概率分布替代另一个时的信息损失。然后利用该散度通过以下表达式更新信任值：
$$ W_n= \frac{1}{1+\sqrt{D_n}}. \quad (11) $$

5.2.3. 使用二手信息

在先前分析的信任管理方案中，每个传感器的信任值由担任信任方角色的设备（通常是转发节点）进行计算和更新。然而，当信任方不在其受信者i的传输范围内时，它可能需要依赖其邻居Ni提供的信息来计算其可信度。包等人 [2012]通过引入两种不同的信任更新准则来解决这一问题：
$$ T_{ij}(t)=\begin{cases} (1 - \alpha)T_{ij}(t - \delta t)+ \alpha T_{ij}(t) & \text{if } j \in N_i \ \text{avg} {k \in N} {(1 - \gamma)T {kj}(t - \delta t)+ \gamma T_{kj}(t)} & \text{otherwise}. \end{cases} \quad (12) $$

第二种情况的计算表示节点j的推荐信息，即从转发的信息中提取出的可信度。最终，推荐信息依赖于直接邻居的可信度。然而，这种可信度可能被恶意节点操纵，以诋毁或褒扬其他节点。包等人[2012]通过参数 γ控制推荐信息的影响来缓解此问题，该参数设置为 βTik（t）1+βTik（t）。因此，如果一个传感器的可信度相对于参数 β较低，则其推荐信息的贡献将很小。然而，实施开‐关攻击的传感器可以在短时间内给出虚假推荐信息，然后再次正常行为而不被检测到。

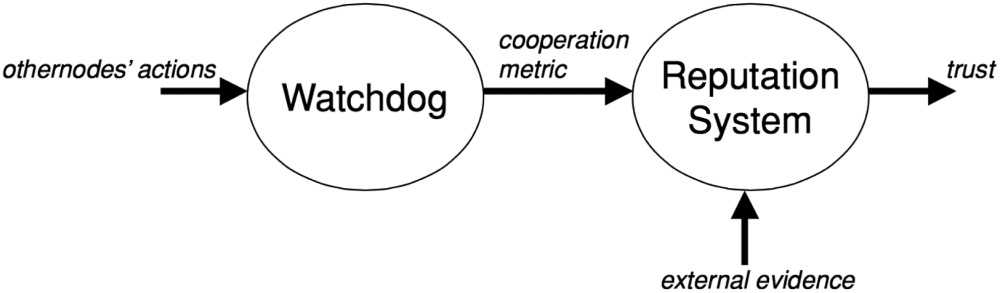
即使存在直接信息，也可以将推荐信息作为二手信息，并与直接信息相结合以获得声誉。二手信息能够加快信任值的收敛速度，但会增加网络流量开销，并引入新的问题，例如推荐信息的权重准则和推荐交换频率[Huang 等人 2006]。Ganeriwal 等人[2003]采用这种方法，将声誉视为概率分布，通过直接声誉和间接声誉的组合进行更新。直接声誉基于看门狗模块进行更新，而间接声誉则通过来自其他节点的推荐信息（即其他节点的声誉）进行更新。该框架的方案如图7所示。需要注意的是，这种声誉定义方式会引入一个循环：间接声誉来自其他传感器提供的声誉，而这些声誉又依赖于间接声誉。为避免信息循环，推荐信息应仅从直接观察者获取。

将声誉建模为单个值并未考虑传感器在信任另一个传感器时的不确定性。该信息在处理推荐信息时尤为有用，因为来自具有高不确定性的传感器的推荐信息应具有较小的贡献。为了考虑不确定性，声誉可以使用概率分布进行建模，其分布的选择主要由信任评估和更新准则决定。例如，Ganeriwal 等人 [2003] 使用 beta distribution，因为在将节点间的二元交互建模为二项分布时，贝塔分布是后验分布。Momani 等人[2008]应用正态分布来建模两个传感器测量值之间的差异（假设空间同质性；参见第4.4节）。

6. 恶意数据注入的诊断与特征分析

检测测量值偏离预期行为通常不足以推断数据注入攻击的存在。以异常检测为例，我们已经看到测量值仅被分类为离群或非离群，而恶意数据注入只是导致离群数据的可能原因之一。一般来说，无论采用何种技术来检测偏离预期行为的情况，都需要找出该偏差的原因。我们将此任务称为诊断。通常，这并非一项简单的任务，因为不同的原因（如故障或真实事件）可能会产生类似的影响。

此外，即使能够确切判断攻击的存在，仍需要进一步的信息来确定应采取的应对措施。例如，需要了解攻击的影响以及受攻击影响的系统区域（节点）。我们将此另一项任务称为对攻击的特征分析。

接下来，我们分析无线传感器网络中恶意数据注入的诊断与特征分析的最新研究进展。

6.1. 诊断

无线传感器网络中恶意数据注入的诊断包括将其与两种可能产生类似预期行为偏差的主要现象区分开来：故障和感兴趣事件。故障代表由环境中的障碍物、传感器电池耗尽、污染和污垢等因素引起的非故意误差。感兴趣事件代表很少出现但具有重要意义的环境条件，因为它们可能揭示警报场景，例如心脏病发作、火灾和火山喷发。

有关异常或不可信传感器原因的信息可能非常宝贵。通过掌握问题性质的细粒度知识，可以获得适当的响应来解决问题。然而，截至目前分析的论文中，仍缺乏一个全面的诊断阶段。大多数研究的关注重点在于诊断事件而非故障。用于区分两者的普遍假设是：故障很可能是随机无关的，而事件的测量值则很可能具有空间相关性[Luo 等，2006； Shahid 等人2012]。需要注意的是，这一假设将共模故障排除在了分析之外。基于此假设，在利用时间[Bettencourt 等人 2007；Shahid 等人 2012]或属性[Shahid 等人 2012]相关性检测到与预期数据的偏差后，可通过利用空间相关性来诊断该偏差是由故障还是由事件引起的。当一组传感器对某一事件的存在达成共识时，那些不一致的传感器将被视为有故障的[Luo 等，2006；Shahid 等，2012；Bettencourt 等人 2007]。类似地，某些感知属性（例如人体生命体征，如血糖水平、血压等）在无故障情况下可被认为是高度相关的，而故障反而会破坏这些属性之间的相关性。此时，如果我们进一步假设事件只会导致最少数量的异常属性，则当异常属性数量未达到该最小值时，便可识别为故障[萨勒姆等人 2013]。

相较于故障和事件，针对恶意干扰的诊断进展较少。我们将在以下章节中对其进行总结。

6.1.1. 区分恶意干扰与事件

在文献中，通过基于共识的策略 [Liu et al. 2007；阿塔克利等人 2008；Wang 等，2010；Oh 等人 2012；林和崔 2013；孙等人 2013] 来区分恶意干扰与事件；即首先利用传感器的信息判断事件是否存在，然后将未支持最终决策的传感器识别为恶意。该方法基于这样一个假设：传感器之间具有足够的空间相关性，能够正确检测事件。然而，多个受损节点也可能协同攻击，以保持它们之间的空间相关性一致。这使得区分真实事件与恶意数据注入变得更加复杂，并允许攻击者制造虚假事件或掩盖真实事件。这一问题将在第6.2节中进一步详细讨论。

6.1.2. 区分恶意干扰与故障

用于区分恶意数据注入与故障的标准较少被提及。可以识别出两种主要方法：将诊断委托给入侵检测技术，以及利用故障统计。

入侵检测。 使用基于异常的技术检测攻击的主要挑战之一在于，此类技术抽象了攻击实施的方式。这种选择源于其目标是检测具有未知模式的新攻击，而与之相对的入侵检测技术则是基于识别已知攻击特征。魏等人[2006]提出的框架在异常检测技术与入侵检测系统之间做出权衡，因为检测通过异常检测进行，从而实现高检测率，而诊断则通过入侵检测完成。显然，该方法仅能对已知攻击提供诊断，无法区分未知攻击与故障。

故障统计。 对故障的统计特征分析也可用于将其与恶意干扰区分开来。吴等人[2012]和Lim 和 Choi[2013]利用瞬态故障的预期频率，避免将遭受瞬态故障的传感器从系统中排除。事实上，他们的信任管理算法允许临时的异常行为，使这些传感器能够恢复可信度。只有那些发生更频繁异常行为的传感器，包括恶意传感器和具有永久性故障的传感器，才会被排除。

6.2. 特征描述

如果检测和诊断恶意数据注入回答的是“是否存在攻击？”这一问题，那么特征描述则回答“哪些传感器被破坏？”以及“攻击是如何进行的？”等问题。这种差异在事件检测任务中可能更为明显。例如，在检测到事件存在后，可以使用Wu等人[2007],提出的方法来表征该事件的空间边界，该方法通过寻找来自不同传感器的测量值之间差异较大的区域，从而指示由事件边界引入的不连续性。在这种情况下，特征描述由检测触发，但是一项独立的任务。

6.2.1. 共谋及其影响

在恶意数据注入中，检测、诊断和特征分析通常被同时处理，因为描述攻击的信息对于改进检测非常有价值。特别是当多个传感器已被受损并共谋发动攻击时，它们会协同行动以更改测量值，同时尽可能逃避任何异常检测。因此，识别哪些传感器更可能是正常的，哪些传感器更可能已受损，成为检测攻击本身的重要组成部分。

在合谋攻击中，被破坏的传感器遵循一种联合策略，降低了空间相关性的优势，因为受损节点通过协作生成可信的空间相关数据[塔纳猜维瓦特和赫尔米 2005]。当存在共谋时，诊断也显著变得更加复杂。塔纳猜维瓦特和赫尔米[2005]指出，当出现真实异常（例如与某个事件相关）时，共谋节点的极端读数可能被隐藏。随着（共谋）受损传感器百分比的增加，问题变得愈发困难。最终，当共谋传感器的数量增加到超过正常传感器时，攻击可能仍然可检测，但可能无法区分哪些节点是正常的，哪些节点是受损的。塔纳猜维瓦特和赫尔米[2005]针对共谋节点评估了他们的异常检测算法，发现当超过30%的节点参与共谋时，性能明显下降。查齐安纳基斯和帕帕瓦西里乌[2007]也报告了类似的结果。

Bertino 等人[2014]描述了一种新的攻击场景，该场景适用于通过迭代滤波算法计算可信度的情况。而在通用的（非迭代）信任评估技术中，信任权重的更新仅基于当前时刻的数据以及上一时刻计算出的权重，在迭代滤波中，权重会根据同一时刻的数据进行迭代更新，直到满足收敛准则。在此背景下，作者引入了一种新的攻击场景：除了一个节点外，其余所有共谋节点均在其读数中产生明显的偏差。而剩下的被攻陷节点则报告接近于所有读数（包括恶意测量值）聚合值的值。最终，该节点获得较高的信任值，而其他所有节点的信任值均较低。相应地，聚合值迅速收敛到一个远离正常节点值的值。作者表明，当传感器被赋予相等的初始可信度时，这种攻击是成功的。因此，他们提出将初始可信度计算为一个随误差方差增加而减小的函数。误差定义为与估计的物理属性值 ϕ(t) 的距离，并且对所有传感器而言是相同的。

雷兹瓦尼等人[2013]提出了一种新的技术，该技术用于检测共谋行为而非对抗共谋。该技术基于这样一个假设：正常节点的聚合值偏差服从正态分布。这一假设源于观察到非受损节点的偏差即使较大，也来自大量独立因素，因此大致呈高斯分布。而对于共谋节点，则认为该条件不成立。然后，通过运行柯尔莫哥洛夫‐斯米尔诺夫检验来检查是否符合正态分布，从而区分共谋节点与正常节点。

总之，尽管许多研究提出了新的异常检测算法以适应广泛的应用场景，但相比之下，专门针对传感器之间共谋等更复杂攻击情形下的恶意数据注入问题的研究较少。这类场景在未来还需要进一步探索。

6.2.2. 特征分析 架构：集中式与分布式

为了检测、诊断并识别注入恶意测量值的节点，可以采用不同程度分布化的架构。接下来我们将讨论不同方案的属性。

在无线传感器网络中，始终至少存在一个实体，用于收集系统执行分析、决策和操作所需的测量数据：基站。通常假设基站未被攻陷，因此可用于表征受损节点。在这种情况下，我们采用的是集中式架构，例如查齐安纳基斯和帕帕瓦西里乌 [2007],、阿塔克利等人 [2008],、吴等人 [2012],、Lim 和 Choi [2013], 以及雷兹瓦尼等人 [2013] 所提出的架构。

即使基站是网络中唯一的可信实体，分布式特征化也是可能的。事实上，正如包等人[2012],所提出的，可以在层次结构中对传感器节点进行评估，其中每个节点评估其在层次结构中下方节点的信任度。因此，当能够从某个节点到基站建立一条信任链时，基站就会信任该节点。

当分布原则被推向极端时，每个节点都充当其所有邻居的看门狗，并向基站（或层次结构中的下一个节点）报告警报[Ganeriwal 等，2003；Tanachaiwiwat 和 Helmy 2005； 刘等人 2007]。在收集所有报告后，基于多数投票等算法做出决策[Hinds 2009]。该方法的缺点在于缺乏全局知识，因此对合谋攻击的鲁棒性较差，同时由于看门狗报告带来了显著的网络开销。Tanachaiwiwat 和 Helmy [2005]提出通过部署多个可靠的防篡改传感器节点来探测可疑节点以克服这些问题。然而，这种解决方案需要额外的昂贵硬件，这削弱了无线传感器网络的成本优势。

7. 讨论

在前面的章节中，我们了解了如何应用不同的技术来检测恶意数据注入，这些技术如何利用测量值的相关性，以及这些相关性所基于的假设。我们研究了不同的检测技术，以及它们如何发现与预期行为的偏差。我们强调了区分不同偏差源的重要性，并介绍了迄今为止实现这一目标的主要工作方向。

我们现在通过构建直接比较表来整合这些分析，以总结其主要特征。下一部分将提供上述每种技术所报告结果的汇总。

7.1. 方法比较

我们将迄今为止分析的各种方法的比较分为表II和表III，分别包含异常检测和信任管理技术。从左到右各列内容如下：技术名称及参考文献；用于定义预期数据的相关性；关于空间模型的假设（如有）；所使用的检测准则；可能的异常来源（如论文中所述）；以及提供了诊断准则的情况——例如，{事件},{恶意或有故障的}表示作者给出了区分来自事件的异常与来自恶意或故障传感器的异常的准则。

我们观察到，空间相关性最常被利用，且通常基于均匀空间的假设。这种情况在考虑存在恶意数据注入的论文中尤为明显，这可能是由于通常仅假设一小部分传感器受损。因此，在空间域中，始终存在大量真实测量值可用于检测恶意测量值。

假设空间同质性使得计算显著简化，因为认为传感器测量的是相同的值。然而，这也极大地限制了这些技术在实际场景中的适用性。当物理现象以低精度被观测时，例如大开放区域的整体温度，如果空间变化被公式(2)中的误差项所吸收，则此假设仍然成立。但这样允许攻击者引入处于误差范围内的恶意数据，这些数据仍可能显著偏离真实值。虽然该假设在小区域中通常是合适的，但小区域通常包含较少的传感器，而这些传感器更易被攻击者全部攻破。

当考虑多种相关性时，通常会结合利用时间相关性和空间相关性。属性相关性的使用相对较少，可能是因为理解这些相关性需要了解其物理意义，而这与具体应用相关。表格进一步凸显了诊断和特征分析的缺乏（参见第6节）。很少有论文专门研究涉及共谋的恶意注入，更少的论文处理将其与其他偏差原因区分开来的问题。虽然区分事件与故障是最常被考虑的诊断问题，但区分攻击与故障无疑更具挑战性，且目前仍较为罕见。

7.2. 比较报告的评估结果

在前面的章节中，我们探讨了可用于检测、诊断和表征恶意数据注入问题的技术。针对那些专门关注恶意数据注入的技术，我们现在介绍表IV总结了所有取得的结果以及所有相关的仿真参数。最后三列表示当检测率（DR）分别为0.90、0.95和0.99时的误报率（FPR）。根据定义，检测率（DR）是指正确检测到的攻击实例数量与攻击实例总数之比。误报率（FPR）是指被错误分类为攻击的正常数据实例数量与正常数据实例总数之比。DR与FPR之间的关系被称为接收者操作特性（ROC）。

第2列报告了实验中所用数据集大小的信息。第3列报告了恶意节点或恶意测量值的百分比。第4列报告了算法的输入大小；例如，在一个包含100个节点的实验中，若节点被聚集成每组10个节点，并在簇上运行算法，则算法的输入大小为10。

通常，每篇论文中的测试都是在不同假设场景下进行的。例如，刘等人[2007]为正常传感器生成符合正态分布的数据，为恶意传感器生成另一个正态分布的数据。结果虽然很好，但很大程度上依赖于这两个分布之间的差异。另一个对结果有显著影响的重要假设是空间模型。正如第4.4节中指出的，大多数论文假设传感器读数在空间上是同质的；换句话说，测量值预期是

表IV. 检测性能，独立攻击

Work	数据集大小	恶意数据百分比	输入大小	每个算法执行	FPR 对于 DR=0.90	FPR 对于 DR=0.95	FPR 对于 DR=0.99
扩展卡尔曼滤波器 [孙等人 2013]	10,000 个样本	50% 样本，同一节点	6	0.22	0.42	0.7
刘等人[2007]	4,096 个节点	10%–25% 节点	10	0.01	0.01	0.07
ART [塔纳猜威瓦特 和赫尔米 200